单个偶然误差没有规律，只有大量的偶然误差才有统计规律。要分析偶然误差的统计规律，需要得到一系列的偶然误差Δi。根据式（6.1），应对某个真值已知的量进行多次重复观测才可以得到一系列偶然误差Δi的准确值。在大部分情况下，观测量的真值l～是未知的，这就为我们得到Δi的准确值进而分析其统计规律带来了困难。

但是，在某些情况下，观测量函数的真值是已知的。例如，将一个三角形内角和闭合差的观测值定义为

则它的真值为=0，由式（6.1）真误差的定义，可求得ωi的真误差为

式（6.4）表明，任一三角形闭合差的真误差就等于闭合差本身。

设某测区，在相同条件下共观测了358个三角形的全部内角，将计算出的358个三角形闭合差划分为正误差、负误差，分别在正、负误差中按照绝对值由小到大排列，以误差区间dΔ=±3″统计其误差个数k，并计算相对个数k/n（n=358），称k/n为频率，结果列于表6.1中。

表6.1　三角形闭合差的统计结果

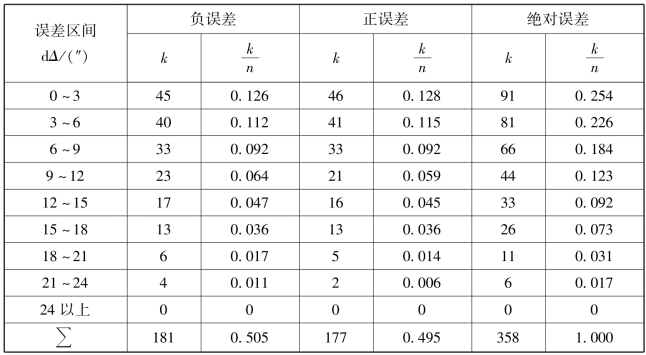
为了更直观地表示偶然误差的分布情况，以Δ为横坐标，以y=为纵坐标作表6.1的直方图，结果如图6.1所示。图中任一长条矩形的面积为等于频率。(www.daowen.com)

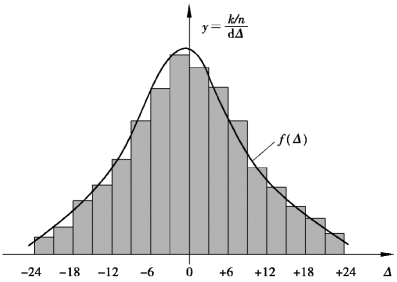
图6.1　偶然误差频率直方图

由图6.1可以总结出偶然误差的4个统计规律如下：

①偶然误差有界，或者说在一定条件下的有限次观测中，偶然误差的绝对值不会超过一定的限值；

②绝对值较小的误差出现的频率较大，绝对值较大的误差出现的频率较小；

③绝对值相等的正、负误差出现的频率大致相等；

④当观测次数n→∞时，偶然误差的平均值趋近于零，即有

式中，[Δ]=Δ1+Δ2+…+Δn=。在测量中，常用[　]表示括号中数值的代数和。