如图4.9所示，光电测距仪是通过测量光波在待测距离D上往、返传播一次所需的时间t2D，根据式（4.15）来计算待测距离D，则

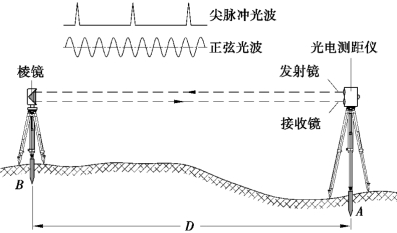
图4.9　光电测距原理

其中，c=为光在大气中的传播速度，c0为光在真空中的传播速度，c0=（299 792 458±1.2）m/s；n≥1，为大气折射率，n是光波长λ、大气温度t和气压P的函数，即

由于n≥1，所以c≤c0，故光在大气中的传播速度要小于其在真空中的传播速度。

红外测距仪一般采用GaAs（砷化镓）发光二极管发出的红外光作为光源，其波长λ=0.85～0.93μm。对一台红外测距仪来说，λ是一个常数。由式（4.16）可知，影响光速的大气折射率n只随大气温度t及气压P而变化，这就要求在光电测距作业中，应实时测定现场的大气温度和气压，并对所测距离施加气象改正。

根据测量光波在待测距离D上往、返一次传播时间t2D方法的不同，光电测距仪可分为脉冲式和相位式两种。

1）脉冲式光电测距仪

脉冲式光电测距仪是将发射光波的光强调制成一定频率的尖脉冲，通过测量发射的尖脉冲在待测距离上往返传播的时间来计算距离。如图4.10所示，在尖脉冲光波离开测距仪发射镜的瞬间，触发打开电子门，此时时钟脉冲进入电子门填充，计数器开始计数。在仪器接收镜接收到由棱镜反射回来的尖脉冲光波的瞬间，关闭电子门，计数器停止计数。设时钟脉冲的振荡频率为f0，周期为T0=1/f0，计数器计得的时钟脉冲个数为q，则有

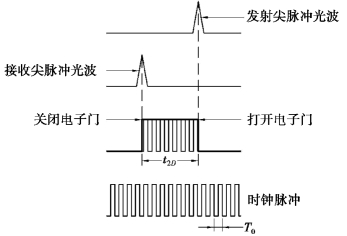
图4.10　脉冲测距原理

由于电子计数器只能记忆整数个时钟脉冲，小于一个时钟脉冲周期T0的时间被计数器丢掉了，这就使计数器测得的t2D最大有一个时钟脉冲周期T0的误差，也即mt2D=±T0。应用误差传播定律（见第6章6.4节），由式（4.15）可以求得电子计数器的计数误差mt2D对测距误差mD的影响为

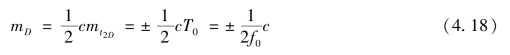
由式（4.18）可知，时钟脉冲频率f0越大，测距误差就越小。取c≈3×108 m，当要求测距误差为mD=±0.01 m时，由式（4.18）可以反求出仪器的时钟脉冲频率应为f0=15 000 MHz。

通常应用石英晶体振荡器（简称石英晶振）来产生时钟脉冲频率，石英晶振工作温度的稳定情况对其频率稳定度有很大影响，且石英晶振的振荡频率越高，对工作温度的稳定度要求也越高。由于制造技术上的原因，目前世界上可以做到并稳定在1×10-6级的石英晶振频率最高为300 MHz，将f0=300 MHz代入式（4.18）求得仪器的测距误差mD=±0.5 m。

由此可知，如果不采用特殊技术测出被计数器舍弃的小于一个时钟脉冲周期T0的时间，而仅仅靠提高时钟脉冲频率f0的方法来使脉冲测距仪达到毫米级的测距精度是困难的。

1985年，徕卡公司推出了测程为14 km、标称测距精度为±（3～5 mm+1 ppm）的DI3000红外测距仪，它是当时测距精度最高的脉冲式光电测距仪，如图4.11所示。根据厂方资料介绍，该仪器采用了一个特殊的电容器用于充、放电，它的放电时间是充电时间的数千倍。测距过程中，由发射和接收的尖脉冲光波控制对该电容器充电t2D时间，然后放电。设放电时间为T2D，利用放电的开始、结束来开关电子门，通过计数填入电子门的时钟脉冲数来解算放电时间T2D。

图4.11　脉冲红外测距仪DI3000

DI3000红外测距仪的时钟脉冲频率f0=15 MHz，其周期为T0=1/f0=6.666 666 67×10-8 s，则通过计数填入电子门的时钟脉冲数求得电容器的放电时间T2D的误差为=±T0=±6.666 666 67×10-8 s。如果放电时间是充电时间的3 000倍（厂方没有提供详细资料），则求得的充电时间t2D的误差为

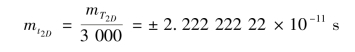(www.daowen.com)

将上式代入式（4.18）可以求得测距误差为mD=±3.3 mm。

2）相位式光电测距仪

相位式光电测距仪是将发射光波的光强调制成正弦波，通过测量正弦光波在待测距离上往返传播的相位移来解算距离。图4.12是将返程的正弦波以棱镜站B点为中心对称展开后的光强图形。

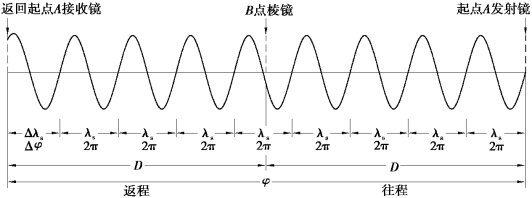
图4.12　相位测距原理

正弦光波振荡一个周期的相位移是2π，设发射的正弦光波经过2D距离后的相位移为φ，则φ可分解为N个2π整数周期和不足一个整数周期相位移Δφ，则有

正弦光波振荡频率f的意义是1 s振荡的次数，则正弦光波经过t2D s后振荡的相位移为

由式（4.19）和式（4.20）可以解出t2D为

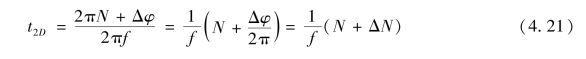
式中，ΔN=0＜ΔN＜1。将式（4.21）代入式（4.15），得

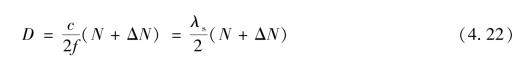
式中，λs=为正弦波的波长，为正弦波的半波长，又称测距仪的测尺。取c≈3×108 m，则不同的调制频率f对应的测尺长列于表4.1中。

表4.1　调制频率与测尺长度的关系

由表4.1可知，f与λs/2的关系是：调制频率越大，测尺长度越短。

如果能够测出正弦光波在待测距离上往返传播的整周期相位移数N和不足一个周期的小数ΔN，就可以按式（4.22）计算出待测距离D。

在相位式光电测距仪中有一个电子部件，称相位计，它能将测距仪发射镜发射的正弦波与接收镜接收到的、传播了2D距离后的正弦波进行相位比较，测出不足一个周期的小数ΔN，其测相误差一般小于1/1 000。相位计测不出整周数N，这就使相位式光电测距方程式（4.22）产生多值解，只有当待测距离小于测尺长度时（此时N=0）才能确定距离值。人们通过在相位式光电测距仪中设置多个测尺，使用各测尺分别测距，然后组合测距结果来解决距离的多值解问题。

在仪器的多个测尺中，称长度最短的测尺为精测尺，其余为粗测尺。例如，一台测程为1 km的相位式光电测距仪设置有10 m和1 000 m两把测尺，由表4.1可查出其对应的调制频率为15 MHz和150 kHz。假设某段距离为586.486 m，则

用1 000 m的粗测尺测量的距离：（λs/2）粗ΔN粗=1 000 m×0.587 1=587.1 m。

用10 m的精测尺测量的距离：（λs/2）精ΔN精=10 m×0.648 6=6.486 m。

精、粗测尺测距结果的组合过程为

精、粗测尺测距结果组合由测距仪内的微处理器自动完成，并输送到显示窗显示，无须用户干预。