视距测量是一种间接测距方法，它是利用测量仪器望远镜内十字丝分划板上的视距丝及刻有厘米分划的视距标尺（地形塔尺或普通水准尺），根据光学原理同时测定两点间的水平距离和高差的一种快速测距方法。其中，测量距离的相对误差约为1/300，低于钢尺量距；测定高差的精度低于水准测量。视距测量广泛应用于地形测量的碎部测量中。

1）视准轴水平时的视距计算公式

如图4.7所示，在A点安置水准仪或经纬仪，B点竖立视距尺，设望远镜视线水平，瞄准B点的视距尺，此时视线与视距尺垂直。

在图4.7中，p=为望远镜上、下视距丝的间距，l=为标尺视距间隔，f为望远镜物镜的焦距，δ为物镜中心到仪器中心的距离。

图4.7　视准轴水平时的视距测量原理

由于望远镜上、下视距丝的间距p固定，因此从这两根丝引出去的视线在竖直面内的夹角φ也是固定的。设由上、下视距丝n，m引出去的视线在标尺上的交点分别为N，M，则在望远镜视场内可通过读取交点的读数N，M求出视距间隔l。如图4.7（b）所示的视距间隔为：l=1.385 m-1.188 m=0.197 m（注：图示为倒像望远镜的视场，应从上往下读数）。

由于△n′m′F相似于△NMF，因此有则

顾及式（4.4），由图4.7得

令K=C=f+δ，则有

式（4.6）中，K为视距乘常数；C为视距加常数。设计制造仪器时，通常使K=100，C接近于零。因此视准轴水平时的视距计算公式为

如图4.7所示的视距为D=100×0.197 m=19.7 m。如果再在望远镜中读出中丝读数v（或取上、下丝读数的平均值），用小钢尺量出仪器高i，则A，B两点的高差为

2）视准轴倾斜时的视距计算公式

如图4.8所示，当视准轴倾斜时，由于视线不垂直于视距尺，因此不能直接应用式（4.7）计算视距。由于φ角很小（约为34′），因此有∠MO′M′=α，也就是说，只要将视距尺绕与望远镜视线的交点O′旋转图示的α角后就能与视线垂直，则有

则望远镜旋转中心O与视距尺旋转中心O′之间的视距为

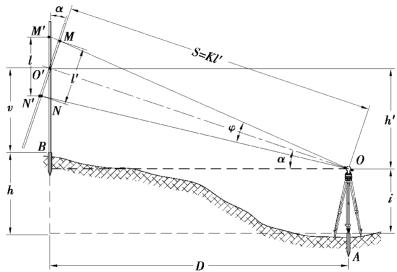
图4.8　视准轴倾斜时的视距测量原理

由此求得A，B两点间的水平距离为

设A，B的高差为h，由图4.8容易列出方程

其中，h′=S sinα=Kl cosαsinα=，或者h′=D tanα。称h′为初算高差，将其代入上式，得高差公式

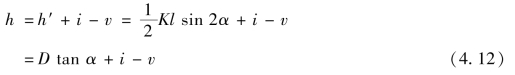
【例4.1】　在A点安置经纬仪，B点竖立水准尺，A点的高程为HA=35.32 m，量得仪器高i=1.39 m，测得上、下丝读数分别为1.264，2.336 m，盘左观测的竖盘读数为L=82°26′00″，竖盘指标差为x=+1′，求A，B两点间的水平距离和高差。

【解】　视距间隔为(www.daowen.com)

竖直角为

水平距离为

中丝读数为

高差为

B点的高程为

可以用下列fx-5800P程序P4-1进行视距测量计算。

程序名：P4-1，占用内存218字节。

执行程序P4-1，计算【例4.1】的屏幕提示与操作过程如下：

3）视距测量的误差分析

（1）读数误差

视距间隔l由上、下视距丝在水准尺上截取的读数相减而得，由于视距乘常数K=100，因此视距丝的读数误差将被扩大100倍地影响所测距离。如果读数误差为1 mm，则视距误差即为0.1 m。因此，在水准尺上读数前应先消除视差，读数时应十分仔细。另外，由于竖立水准尺者不可能使水准尺完全稳定不动，因此上、下丝读数应几乎同时进行。建议使用经纬仪的竖盘微动螺旋将上丝对准水准尺的整分米分划后，立即估读下丝读数的方法；同时还应注意视距测量的距离不能太长，因为测量的距离越长，视距标尺上1 cm分划的长度在望远镜十字丝分划板上的成像长度就越小，其读数误差就越大。

（2）水准尺不竖直误差

当水准尺不竖直且偏离铅垂线方向dα角时，对水平距离影响的微分关系为

目估使水准尺竖直大约有1°的误差，即dα=1°，设Kl=100 m，按式（4.13）计算，当α=5°时，d D=0.15 m；当α=30°时，d D=0.76 m。由此可见，水准尺倾斜对测定水平距离的影响随视准轴竖直角的增大而增大。山区测量时的竖直角一般较大，此时应特别注意将水准尺竖直。视距水准尺上一般装有水准器，立尺者在观测者读数时应参照尺上的水准器来使水准尺竖直及稳定。

（3）竖直角观测误差

竖直角观测误差在竖直角不大时对水平距离的影响较小，主要影响高差，其公式为

设Kl=100 m，dα=1′，当α=5°时，d h=0.03 m。

由于视距测量时通常是用竖盘的一个位置（盘左或盘右）进行观测，因此，事先应对竖盘指标差进行检验和校正，使其尽可能小；或者每次测量之前测定指标差，在计算竖直角时加以改正。

（4）大气折光的影响

近地面的大气折光使视线产生弯曲，在日光照射下，大气湍流会使成像晃动，风力使标尺摇动，这些因素都会使视距测量产生误差。因此，视距测量时，不要使视线太贴近地面（即不要用望远镜照准视距标尺的底部读数），在成像晃动剧烈或风力较大时应停止观测。阴天且有微风时是观测的最有利气象条件。

在上述各种误差来源中，以（1）和（2）两种误差影响最为突出，应充分注意。根据实践资料分析，在良好的外界条件下，距离在200 m以内，视距测量的相对误差约为1/300。