任务描述

杆件受到垂直于轴线的外力或作用面在轴线所在平面内的外力偶作用时，杆件的轴线将由直线变为曲线，这种变形称为弯曲变形。以弯曲变形为主的构件称为梁。

相关知识

一、弯曲的概念

在日常生活中，弯曲的现象是普遍存在的，例如挑重物的扁担和钓鱼的竹竿，在使用中都会发生弯曲。同样，在工程机械中也存在着弯曲。如吊车的主梁，汽车用的钢板弹簧以及火车的车轴在受到横向载荷作用（如图3-25）时，都会产生弯曲变形。弯曲变形的特点是杆件所受的力是垂直于梁轴线的横向力，在其作用下梁的轴线由直线变成曲线。以弯曲变形为主要变形的杆件，称为梁。

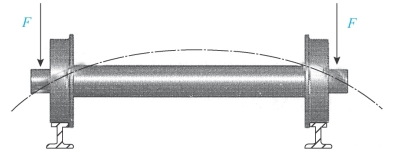
图3-25　车轴在受到横向载荷作用产生弯曲变形

二、平面弯曲

有对称截面的梁，其横截面至少有一个对称轴（如图3-26）。此对称轴与轴线所组成的平面构成一个纵向对称面。如果梁上的所有外力都作用在该梁的纵向对称面内，则梁弯曲变形后，其轴线也必在纵向对称面内弯曲成一条曲线。把这种梁的弯曲变形叫作平面弯曲。

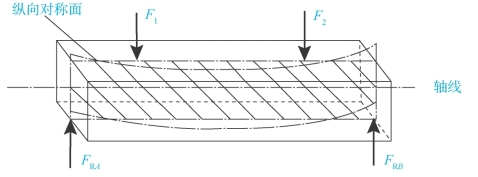
图3-26　横截面至少有一个对称轴

三、梁的基本形式

梁的支承和受力很复杂，计算中常将梁简化为三种典型形式：

（1）简支梁

一端固定铰支承，另一端可动铰支承的梁，如图3-27（a）所示。

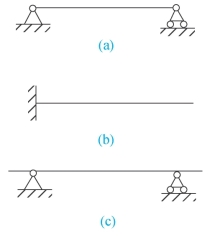
图3-27　梁的基本形式

（2）悬臂梁

一端固定铰支承，另一端自由的梁，如图3-27（b）所示。

（3）外伸梁

具有一个或两个外伸部分的梁，如图3-27（c）所示。

四、梁的内力（剪力与弯矩图）

梁的内力包括剪力FQ和弯矩M，下面以简支梁（如图3-28）为例加以说明。

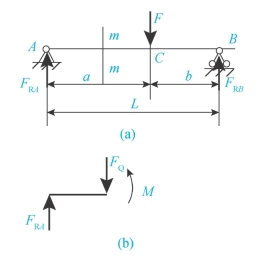
图3-28　简支梁

1.首先求出梁上所受约束反力

FRA=F·b/L

FRB=F·a/L

2.用截面法求内力

①在截面m-m处假想地把梁切为两段。

②取左段为研究对象。由于左段作用着约束反力FRA，则在截面上必有一与FRA大小相等、方向相反的力FQ。由于该内力切于截面，因此称为剪力。又由于FRA与FQ形成一个力偶，因此在截面处必存在一个内力偶M与之平衡，该内力偶称为弯矩。

③建立平衡方程：

由∑F=0，得

FRA-FQ=0，FQ=FRA。

由∑M=0，得

M=FRA·x。

由此可以看出，弯曲时，梁的横截面上产生两种内力：一个是剪力，一个是弯矩。

3.剪力和弯矩符号的规定（如图3-29）

剪力符号规定：左上、右下为正，反之为负。

弯矩符号规定：使梁弯段上凹为正，反之为负。

4.建立剪力、弯矩方程，绘制剪力、弯矩图

一般情况下，在梁的不同截面上，剪力FQ和弯矩M是不相同的，并随着横截面位置的不同而改变。若以横坐标x表示横截面在梁轴线上的位置，则剪力和弯矩皆可表示为x的函数，即

上面的函数表达式为剪力、弯矩方程。

把FQ、M沿x轴的变化情况用图线在坐标内表示出来，所得到的图分别称为剪力图和弯矩图。下面以实例来说明。

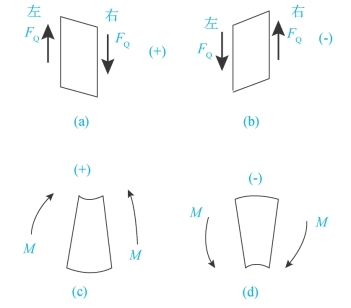
图3-29　剪力和弯矩符号的规定

【例3-7】图3-30所示简支梁受集中力F作用。试列出它的剪力方程和弯矩方程，并作剪力图和弯矩图。

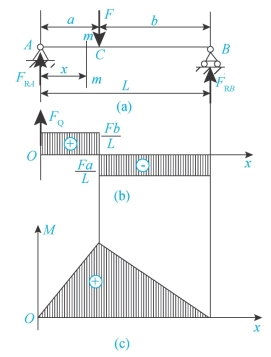
图3-30　例3-7图

解：（1）求支反力

由静力学平衡方程∑MB=0，∑MA=0，可知：

FRA=F·b/L，FRB=F·a/L

（2）列FQ、M方程

在AC段距左端为x的任意截面m-m处将梁截开，由于左端只有FRA，则该截面上的FQ、M分别为

FQ（x）=FRA=F·b/L，（0＜x＜a）

M（x）=FRAx=F·b·x/L，（0≤x≤a）

如在CB段内取距左端为戈的任意横截面，截面以左有FRA和F两个外力，截面上的剪力和弯矩方程为

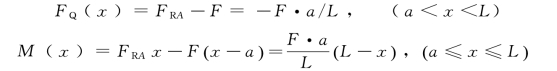
（3）作FQ、M图

在AC段，梁的任意横截面上的剪力FQ为常数F·b/L，符号为正，即剪力图为在x轴上方且平行于x轴的一条直线。同理，BC段也平行x轴，由于FQ值为负，直线在x轴下方。

从剪力图可看出，当a＜b时，最大剪力为

|FQmax|=F·b/L

在AC段，弯矩是x的一次函数，弯矩图为一条斜线，只要确定直线上两点即可确定。由M（x）=Fb/L（x）得M（0）=0，M（a）=F·a·b/L，于是过此两点可作出AC段弯矩图。同理可画出CB段弯矩图。从弯矩图上可以看出，最大弯矩发生在截面C上，即

|Mmax|=F·a·b/L

【例3-8】悬臂梁AB如图3-31（a）所示，在自由端A处作用有集中载荷F，试画出此梁的剪力图和弯矩图。

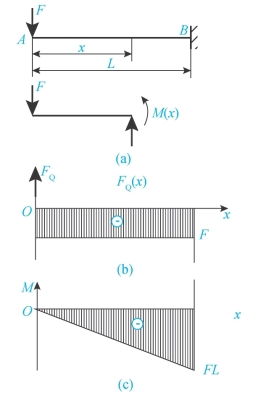(www.daowen.com)

图3-31　例3-8图

解：（1）列剪力方程和弯矩方程

在梁上任意截面左端x处将梁截断，取左侧为研究对象。由于左侧只有一个外力F作用，于是剪力方程和弯矩方程为：

FQ（x）=-F

M（x）=-F·x

（2）画FQ、M图

由剪力方程可知，FQ（x）为负值，因此，FQ图为一纵坐标为-F的水平线，如图3-31（b）所示。

由弯矩方程可知：M（x）为x的一斜直线，如图3-31（c）所示，其位置由两端面的弯矩值决定，即M（0）=0，M（L）=-FL。通过该两点，在弯矩图坐标系中连线，则该斜线即为梁的M图。在剪力和弯矩图中，可以很容易找到梁上受到的最大剪力值和弯矩值，从而找到弯曲受力危险点。由于剪力在梁上都相同，故

|FQmax|=F

而最大弯矩值在固定端B截面处，且有

|Mmax|=F·L

五、梁的强度

1.纯弯曲

梁上各横截面内剪力为零、弯矩为常数时的弯曲变形，称为纯弯曲。

2.正应力

在梁表面画上均匀的横线和纵线，然后在梁的纵向对称面内施加一对力偶M（如图3-32）。观察梁的弯曲变形可知：

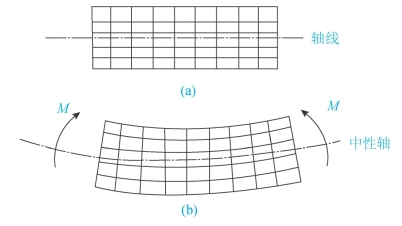
图3-32　正应力实验图

（1）横线仍为直线，且仍与纵线正交，但转了一个角度；

（2）所有纵线变为圆弧线，梁上部凹边纵线缩短，下部凸边纵线伸长。

因此，可以假想梁是由无数根纤维组成，梁下部纤维伸长是由于受拉所致，上部凹边缩短为受压所致。各纤维之间相互挤压，而在受拉区（下部）和受压区（上部）之间存在一层既不伸长也不缩短的纵向纤维层，称为中性层。中性层与横截面的交线称为中性轴。弯曲变形时，横截面绕中性轴旋转。在纯弯曲时，横截面上每点处的应力与变形（伸长或缩短）情况和轴向拉、压时的情况相同。在梁上部凹边压缩最大，压应力最大；梁下部凸边拉伸最大，拉应力也最大；因中性层既不伸长也不缩短，所以中性层的正应力为零。由此可见，梁的横截面上任意点的正应力与该点到中性轴的距离成正比。

弯曲正应力计算公式为

式中，σ——横截面上任一点处的弯曲正应力；

M——该横截面上的弯矩；

y——该点到中性轴的距离；

IZ——该横截面对中性轴的截面二次矩。

3.最大正应力

当式（3-24）中y取最大值ymax（即横截面上、下边缘）时有最大正应力：

令

则有

式中，WZ——抗弯截面系数。

4.梁的强度

为保证梁安全可靠，应使梁的最大正应力不超过梁的许用正应力，即

式中，［σ］——梁的许用应力。

式（3-26）即为梁的强度条件公式。

【例3-9】螺栓压紧装置如图3-33（a）所示。已知板长a=50mm，压板材料的弯曲许用应力［σ］=160MPa，工件所需夹紧力F=3kN，试校核压板的强度。

解：压板可简化为图3-33（b）所示的外伸梁。由梁外伸部分BC可以求得截面B的弯矩MB=F·a，而A、C两截面上的弯矩等于零，弯矩图如图3-33（c）所示。由弯矩图可知，B截面上弯矩最大，且Mmax=MB=F·a=150N·m。

根据截面B的尺寸可求得

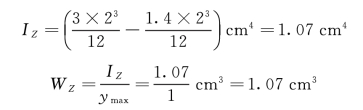
根据抗弯强度条件公式得

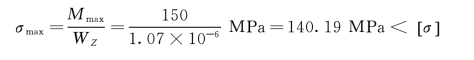
由此可知，螺栓压板有足够的强度。

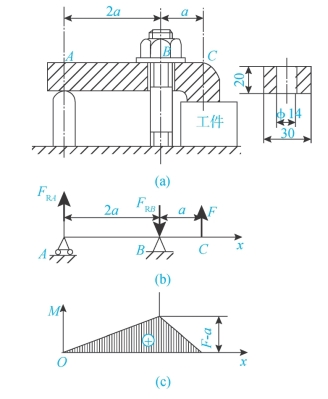
图3-33　梁的横截面上任意点的正应力与该点到中性轴的距离成正比

六、提高抗弯能力的方法

梁的强度越高，抵抗弯曲的能力也就越强。由梁的弯曲正应力σmax=Mmax/WZ≤［σ］可知，要提高梁的强度必须从以下三个方面考虑：选用合理的截面形状，提高抗弯截面系数WZ；注意受力情况，降低最大弯矩Mmax；根据材料性能和弯矩大小选择截面。

1.梁的截面形状

梁的截面形状有圆形、矩形、槽形、工字形等。选用合理的截面，调节截面几何形状，可达到提高强度和节省材料的目的。同样大小的截面积，做成槽形和“工”字形比圆形和矩形抗弯能力强。汽车的大梁由槽钢制成，铁路的钢轨制成工字形，都是从提高抗弯能力和节省材料方面来考虑的。

2.合理布置载荷

作用在梁上的载荷常见的有如下3种。

①集中载荷作用。在结构允许的条件下，将集中载荷变为均布载荷，可提高其抗弯能力。

②适当调整梁的支座位置，也可降低最大弯矩值，例如简支梁通过向内移动支座变为外伸梁。

③将集中载荷靠近支座可降低最大弯矩值，从而提高了抗弯能力。

3.采用变截面梁

汽车上用的钢板弹簧就是变截面梁的应用（如图3-34）。同样，工程上常见的阶梯轴，可大量节省材料，设计也更加合理。

图3-34　汽车上用的钢板弹簧

4.提高抗弯刚度的措施

工程上除了要满足构件强度要求外，还要满足刚度的要求。刚度是梁抵抗变形的能力，刚度越大变形越小。提高刚度的常用措施有：

①缩短梁的长度；

②在不能缩短梁长度的情况下，增加梁的支承约束；

③改变梁的截面形状，尽可能采用“工”字形、箱形薄壁构件。