任务描述

扭转变形是指杠杆受到大小相等、方向相反且作用平面垂直于杠杆轴线的力偶作用，使杠杆的横截面绕轴线产生转动。

相关知识

一、扭转的概念

工程中，很多传动机构中的回转件都会产生扭转变形。例如汽车方向盘转动时，转向轴的受力情况为：司机在方向盘上作用着一个力偶，同时在转向轴下端作用一个阻碍方向盘转动的反力偶。转向轴由于受到这两个力偶的作用，将引起扭转变形。杆件的扭转变形特点是：

①在杆件两端受到大小相等，方向相反的一对力偶的作用；

②杆件上各个横截面均绕杆件的轴线发生相对转动。

在工程中，以扭转变形为主要变形的杆件称为轴，上、下两截面所扭转过的角度称为相对扭转角，如图3-18所示。

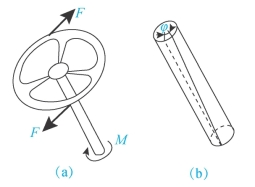
图3-18　相对扭转角

二、圆轴扭转的外力矩计算

对于传动轴等转动杆件，通常只给出其转速和所传递功率，在分析内力时，首先需要根据转速和功率计算外力偶矩。由理论力学可知，力偶在相应角位移上作功，而力偶在单位时间内所作功率P等于其力偶矩M与相应角速度ω的乘积，即

P=Mω

在工程实际中，功率P的常用单位为kW（千瓦），转速n的常用单位为r/min（转/分），在这种情况下，上式即变为

P×103=M×2πn/60

由此得力偶矩

三、扭矩计算

1.内力

求圆轴扭转时的应力——截面法。图3-19所示为受一对外力偶作用的圆轴。假想地沿轴的某一截面m-m切开，并取Ⅰ部分为研究对象。

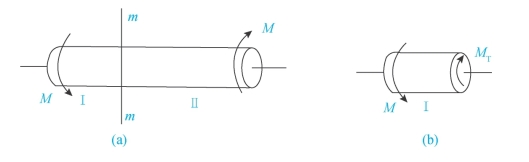
图3-19　受一对外力偶作用的圆轴

为使Ⅰ部分仍处于平衡状态，必在截面m-m处作用一个内力偶矩MT。

建立平衡方程：∑M=0，则

上式表明，圆轴扭转时横截面上的内力是一个力偶矩，称为扭矩。

2.符号规定

按右手螺旋法则，四指方向与截面力偶方向一致，则拇指指向为扭矩的方向（如图3-20）。

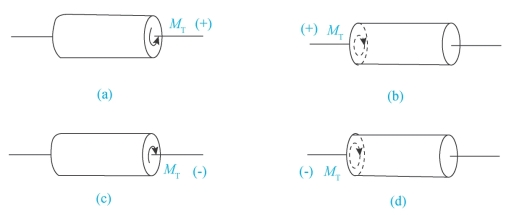
图3-20　右手螺旋法则

当该矢量MT方向与截面外法线方向一致时，MT为正；矢量MT方向与截面外法线方向相反时，MT为负。

四、圆轴扭转时的应力分析

1.扭转现象与假设

如图3-21所示，在圆轴的表面上画出很多等距的圆周线和轴线平行的纵向线，形成大小相等的矩形方格。当圆轴扭转变形时，可以看到：

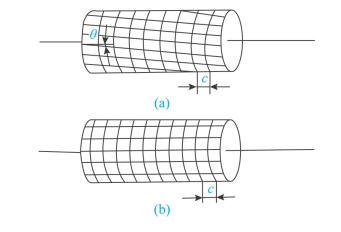
图3-21　在圆轴的表面上画出很多等距的圆周线和轴线平行的纵向线

①各圆周线相对于轴线旋转了一个角度，但其形状大小及圆周线间距没有变；

②各纵向线，均倾斜了一个小角度，矩形变成了平行四边形。

由以上的观察，可得出圆轴扭转时的基本假设：扭转时，圆轴的横截面始终为平面，形状、大小都不改变，只有相对轴线的微小扭转变形，因此在横截面上无正应力，而只有垂直于半径的切应力。

2.切应力分布规律

圆轴横截面上任一点的切应力与该点所在圆周的半径成正比，方向与过该点的半径垂直，切应力最大处发生在半径最大处。应力分布规律如图3-22所示。

3.切应力计算公式

根据静力学关系导出切应力计算公式为

式中，MT——横截面上的扭矩；

ρ——横截面上任意一点的半径；

IP——横截面上截面二次极矩。(www.daowen.com)

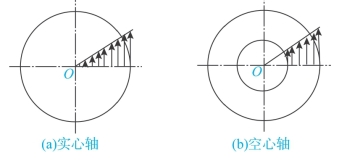
图3-22　应力分布规律

当ρ=R时，切应力最大，即

令IP/R=Wt，于是上式可改写成

式中，Wt表示抗扭截面系数。

4.IP和Wt的计算

（1）实心圆轴

截面二次极矩：

抗扭截面系数：

（2）空心圆轴

截面二次极矩：

抗扭截面系数：

式中，α=d/D。

五、圆轴抗扭强度条件

为了保证受扭圆轴能正常工作而不致破坏，应使圆轴内的最大工作切应力不得超过材料的许用切应力［τ］，即

轴扭转时多受动载荷作用，因此［τ］取值应比静载下的许用应力低些。

【例3-6】汽车传动轴AB（如图3-23）由无缝钢管制成。该轴外径D=90mm，壁厚t=2.5mm，

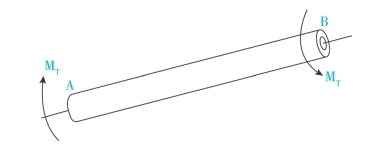
图3-23　汽车传动轴

工作时的最大扭矩MTmax=1.5kN·m。材料的许用切应力［τ］=60MPa，试校核轴AB的强度。如果轴AB设计成实心轴，直径应为多少？

解：（1）计算AB轴的抗扭截面系数

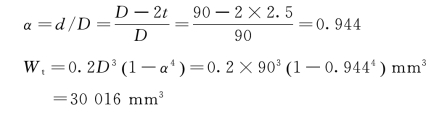
（2）计算轴的最大切应力并校核强度

因为轴AB是等截面轴，且在全轴所有横截面上的扭矩为常量，所以轴AB上任一截面的周边点都是危险点，即周边任一点的切应力都是最大切应力。根据强度条件式

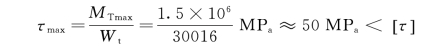
故轴AB满足强度要求。

（3）设计实心圆轴直径D1

因两轴等强度，故实心轴的最大的切应力也应等于50MPa，即

实心轴的直径D1应取直径标准55mm。

六、提高抗扭能力的方法

由扭转强度条件

可知，要提高轴的强度，只有降低τTmax值或提高Wt值两种途径。

1.提高抗扭截面系数Wt

对于圆轴来说，合理截面一个是实心轴，另一个是空心轴。由于Wt与直径D成三次方正比，因此增大轴径效果最为显著。而采用空心轴，在相同截面积的前提下，可以大大提高轴的抗扭截面系数，有效提高轴的扭转强度。

2.降低最大扭矩MTmax

如图3-24（a）所示，已知该轴传递扭矩MA=5N·m，MB=2N·m，MC=3N·m，MD=10N·m，转向如图所示。如果将MD的位置移到MA与MB之间，如图3-24（b）所示，则该轴所受到的MTmax将比图3-24（a）减小一半。所以合理安排轴上零件的位置，将可降低轴的最大扭矩。

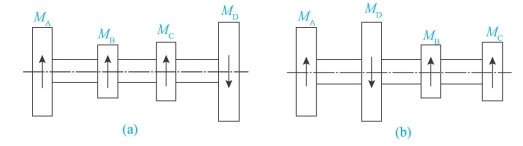
图3-24　轴传递扭矩