任务描述

拉伸和压缩是工程结构构件的基本变形形式之一。在工程计算中，对于拉杆通常只要求保证其具有足够的强度，即工作应力不超过容许应力（材料的破坏应力除以安全系数）；必要时也要求控制其变形量。对于压杆，其正常工作的条件往往不是受强度控制，而是受稳定性控制。

相关知识

一、内力与截面法

1.内力的概念

杆件在外力作用下产生变形，其内部相互间的作用力称为内力。这种内力将随外力增加而增大。当内力增大到一定限度时，杆件就会发生破坏。内力是与构件的强度密切相关的，拉压杆上的内力又称为轴力。

2.截面法

将受外力作用的杆件假想地切开，用以显示内力的大小，并以平衡条件确定其合力的方法，称为截面法。它是分析杆件内力的唯一方法，具体求法如下。

图3-1所示为受拉杆件，假想沿截面m-m将杆件切开，分为Ⅰ和Ⅱ两段。取Ⅰ段为研究对象。在Ⅰ段的截面m-m上到处都作用着内力，其合力为FN。FN是Ⅱ段对Ⅰ段的作用力，并与外力F相平衡。由于外力F的作用线沿杆件轴线，显然，截面m-m上内力的合力也必然沿杆件轴线。据此，可列出其平衡方程：

图3-1　受拉杆件

FN-F=0

得

FN=F

综上所述，求杆件内力的方法——截面法可概述如下。

①截：在需求内力的截面处，沿该截面假想地把构件切开。

②取：选取其中一部分为研究对象。

③代：将截去部分对研究对象的作用，以截面上的未知内力来代替。

④平：根据研究对象的平衡条件，建立平衡方程，以确定未知内力的大小和方向。

【例3-1】如图3-2（a）所示，设一杆沿轴线同时受力F1、F2、F3的作用，其作用点分别为A、C、B，求杆各横截面上的轴力。

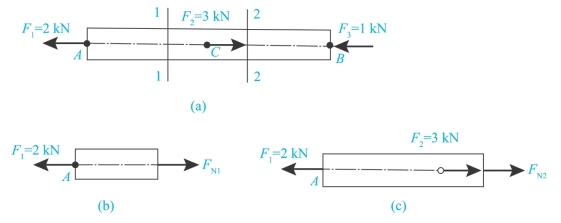
图3-2　受力简图

解：由于杆上有三个外力，因此在AC段和CB段的横截面上将有不同的轴力。

如图3-2（b）在AC段内的任意处以横截面1-1将杆截为两段，取左段为研究对象，将右段对左段的作用以内力FN1代替。由平衡条件可知FN1必与杆的轴线重合，方向与F1相反，为拉力。并由平衡方程

这就是AC段内任一横截面上的内力。

同样用横截面2-2将杆截开，仍取左段为研究对象，如图3-2（c）所示，由平衡方程

得

结果中的负号说明，该截面上内力的方向应与原设的方向相反，即FN2为压力，其值为1kN，此即CB段内任一横截面上的内力。

二、拉伸与压缩的受力、变形特点

在生产实践中，受到拉伸或压缩的杆件虽然外形各有差异，但构件都是直杆，因此在计算中都可以简化为图3-3所示的受力简图。

由图3-3可见，杆件拉伸和压缩的受力特点是：作用于杆件上的外力合力的作用线沿杆件轴线。变形特点是：沿轴线方向产生纵向伸长或缩短。凡以轴向伸长为主要变形特征的杆件称为拉杆，以轴向压缩为主要变形特征的杆件称为压杆。但是仅确定了拉伸或压缩杆件的轴力还不能解决杆件的强度问题。因为同样的轴力，作用在不同大小的横截面上，会产生不同的结果。例如，用两根材料相同而截面尺寸不同的杆件做拉伸试验，使二者承受的轴力始终相同，随着外力的增加，则截面尺寸小的杆件首先被拉断。可见杆件的强度不仅与轴力有关，而且与截面尺寸有关。工程上常用单位面积上的内力来比较和判断杆件的强度。内力是连续分布在截面上的，应力描述了内力在截面上的分布情况和密集程度，它才是判断杆件强度是否足够的根据。

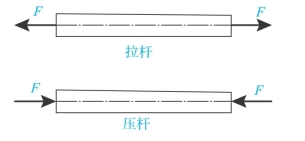
图3-3　杆件拉伸和压缩的受力特点

要确定应力，必须了解内力在横截面上的分布情况。一般认为，杆件横截面上的内力是均匀分布的。根据应力的定义和横截面上应力均匀分布的规律，可以得到

式中，σ——横截面上的应力；

FN——横截面上的轴力；

A——横截面面积。

式（3-1）即为轴向拉伸和压缩时横截面上应力的计算公式。由于分布在横截面上的内力皆垂直于截面，此时的应力也必然垂直于截面，这种垂直于截面的应力，称为正应力。当轴力为拉力时，截面上的应力为拉应力；轴力为压力时，截面上的压力为压应力。通常以正号表示拉应力，以负号表示压应力。

【例3-2】圆截面杆如图3-4（a）所示，已知F1=400N，F2=1000N，d=10mm，D=20mm，试求圆杆横截面上的正应力。

解：由于该杆AB段和BC段的横截面面积不同，所以正应力不相等，应分段计算。

（1）计算各段内的轴力

AB段：取1-1截面左段为研究对象，如图3-4（b）所示，列平衡方程式：

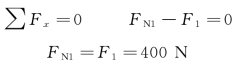
BC段：取2-2截面左段部分，如图3-4（c）所示，

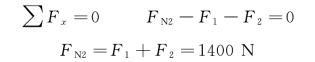
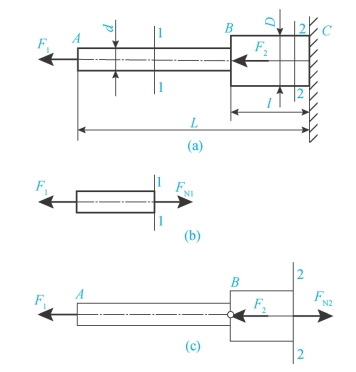
图3-4　圆截面杆

（2）计算各段正应力

AB段：

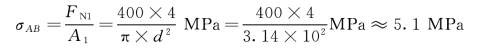
BC段：

当拉（压）杆受到轴力作用后，杆中横截面上的任一点都将产生正应力σ，同时该点相应地产生纵向线应变ε。正应力σ表示为

σ=FN/A(www.daowen.com)

线应变ε为单位长度的伸长量。正应力σ与线应变ε存在下列关系：

式中，E为比例系数，称为弹性模量。在一定的范围内，一点处的正应力同该点处的线应变成正比关系。式中E的量纲与正应力σ的量纲相同，E的常用单位为MPa或GPa。式（3-2）称为胡克定律，适用于单向拉伸、压缩。

拉杆伸长量可用下式计算：

式中，FN——轴力；

L——杆长；

E——弹性模量；

A——杆件的横截面积。

式（3-3）的应用条件为：在杆长L范围内，FN、E、A分别为常量。式（3-3）是胡克定律的另一表达式。

三、拉伸（压缩）时材料的力学性质

材料的力学性质，主要是指材料受力时在强度、变形方面表现出来的性质。材料的力学性质是通过试验手段获得的。试验采用的是国家统一规定的标准试件，如图3-5所示，L0为试件的试验段长度，称为标距。下面以低碳钢和铸铁分别为塑性和脆性材料的代表做试验。

图3-5　国家统一规定的标准试件

1.低碳钢拉伸时的力学性质

试验时，试件在受到缓慢施加的拉力作用下，试件逐渐被拉长L1（伸长量用ΔL来表示），直到试件断裂为止。这样得到F与ΔL的关系曲线，称为拉伸图或F—ΔL曲线，如图3-6所示。拉伸图与试件原始尺寸有关，受原始尺寸的影响。为了消除原始尺寸的影响，获得反映材料性质的曲线，将F除以试件的原始横截面积A，得正应力σ=F/A，把ΔL除以L得应变ε=ΔL/L。以σ为纵坐标，以ε为横坐标，于是得到σ与ε的关系曲线，称为应力-应变图或σ-ε曲线。由σ-ε图（图3-7）可见，整个拉伸变形过程可分为四个阶段。

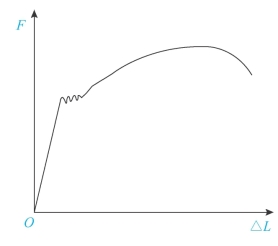
图3-6　拉伸图或F-ΔL曲线

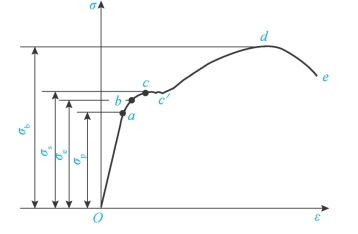
图3-7　σ-ε图

（1）弹性阶段

在拉伸的初始阶段Oa为一直线段，它表示应力与应变成正比关系，即σ∝ε直线最高点a所对应的应力值σP，称为材料的比例极限。低碳钢的比例极限σP≈200MPa。ab段图线微弯，说明σ与ε不再是正比关系，而所产生的变形仍为弹性变形。b点所对应的应力值σe称为材料的弹性极限。由于σP与σe非常接近，因此工程上常不予区别，并多用σP代替σe。

（2）屈服阶段

当由b点逐渐发展到c点，然后再由c至c'点，表明应力几乎不增加而变形急剧增加，这种现象称为屈服或流动，cc'称为屈服阶段。对应c点的应力值σS称为材料的屈服点。低碳钢的σS≈240MPa。材料屈服时，所产生的变形是塑性变形。当材料屈服时，在试件光滑表面上可以看到与杆轴线成45°的暗纹［图3-8（a）］，这是由于材料最大剪应力作用面产生滑移造成的，故称为滑移线。

（3）强化阶段

经过屈服后，图线由c'上升到d点，这说明材料又恢复了对变形的抵抗能力。若继续变形，必须增加应力，这种现象称为强化。c'd段称为强化阶段。最高点d所对应的应力σb称为材料的强度极限。低碳钢的强度极限σb≈400MPa。

（4）局部变形阶段

当图线经过d点后，试件的变形集中在某一局部范围内，横截面尺寸急剧缩小（图3-8b），产生缩颈现象。由于缩颈处横截面显著减小，使得试件继续变形的拉力反而减小，直至e点试件被拉断。de段称为局部变形阶段。

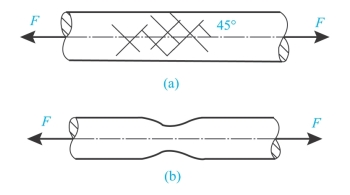
图3-8　低碳钢拉伸时的力学性质

2.铸铁拉伸时的力学性质

从灰铸铁拉伸时的σ-ε曲线（如图3-9）可以看出，从开始至试件拉断，应力和应变都很小，没有屈服阶段和缩颈现象，没有明显的直线段。在工程实际中，当σ-ε曲线的曲率很小时，常以直线代替曲线σ-ε，近似地认为材料服从胡克定律。直线的斜率E=tanα，称为弹性模量。拉断时的最大应力σb为材料的强度极限。由于脆性材料的抗拉强度σb很低，不易用作受拉杆件的材料。

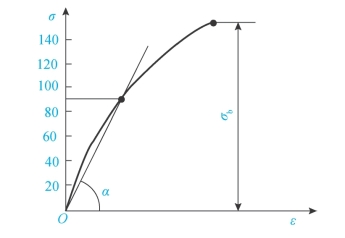
图3-9　灰铸铁拉伸时的σ-ε曲线

3.材料压缩时的力学性质

图3-10为低碳钢压缩时的σ-ε曲线。将此图与低碳钢拉伸的σ-ε曲线相比较（虚线所示），在屈服阶段前，弹性模量E、比例极限σP、屈服点σS与拉伸时基本一致。屈服阶段后，试件越压越扁，曲线上升不到强度极限（如图3-11）。铸铁压缩时的σ-ε曲线与铸铁拉伸时的σ-ε曲线相比（虚线所示），其抗压强度极限σbc远远大于拉强度极限σbt（3～4倍）。压坏时，其断口与轴线约成45°，表明铸铁压缩时沿斜截面相对错动而断裂。由于脆性材料抗压强度σbc很高，常用于受压杆件。

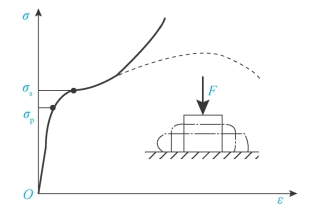
图3-10　低碳钢压缩时的σ-ε曲线

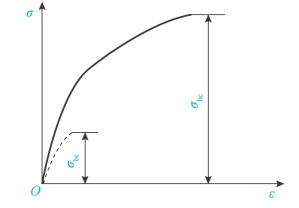
图3-11　屈服阶段后，试件越压越扁，曲线上升不到强度极限

四、许用应力和安全系数

在研究材料的力学性质时知道，当材料受到拉压作用达到或超过材料的极限应力时，材料就会产生塑性变形或断裂，为了保证杆件的安全，必须使杆件在载荷作用下工作的最大应力低于材料的极限应力。极限应力降低到一定程度，这个应力值称为材料的许用应力。许用应力值可由极限应力除以一个大于1的系数而得到。在强度计算中，规定允许的最大应力是极限应力除以一个大于1的系数n。用［σ］表示，即

式中，n为安全系数，它反映了杆件必要的强度储备。在工程实际中，静载时塑性材料一般取安全系数n=1.2～2.5，对脆性材料取2～3.5。安全系数也反映了经济与安全之间的矛盾关系。取值过大，许用应力过低，造成材料浪费。反之，取值过小，安全得不到保证。塑性材料一般取屈服点σs作为极限应力，脆性材料取强度极限σb作为极限应力。

五、拉伸与压缩时的强度校核

为了保证杆件安全可靠地正常工作，必须使杆件的最大工作应力小于材料的许用应力，即

若已知杆件尺寸、载荷及材料的许用应力，可用式（3-6）检验杆件强度是否满足要求。

【例3-3】图3-12所示的拉杆受最大拉力F=300kN，该拉杆的许用应力［σ］=300MPa，直径d=44mm，试校核该拉杆的强度。

解：拉杆受力的情况如图所示，各截面轴力均为

FN=F=300kN

面积为

A=πd2/4

据强度校核公式

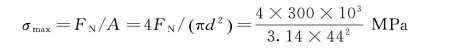
可见σmax＜［σ］，说明拉杆满足拉伸强度要求。

图3-12　例3-3图