2.1.3.1　晶格、晶胞

晶体是内部原子规则排列的物体，但排列的方式有多种。晶体中原子（离子、分子）在空间的规则排列方式称为晶体结构。为便于研究和分析晶体中原子排列的规律性，通常用几何抽象的方法。首先把晶体中的原子看成刚性球体，则晶体就是由许多刚性球体按一定的规律堆垛在一起的，如图2.1（a）所示。然后，将原子抽象为一个几何点，其位置代表原子的中心位置，这些点的空间排列称为空间点阵，将这些几何点用假想直线连接起来，构成一个三维空间的几何格架。这种形象描述原子在晶体中的排列方式的空间几何格架，称为晶格，如图2.1（b）所示。晶格中各连线的交点称为结点或阵点。

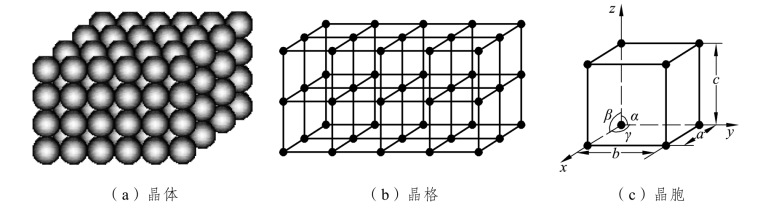
图2.1　晶体、晶格、晶胞示意图

由于晶体周期性重复排列，因此，可在晶体中选取一个能代表原子在空间排列规律的最小几何单元进行分析，这种组成晶格的、能反映晶格特征的最基本的几何单元称为晶胞，如图2.1（c）所示。晶胞通常为平行六面体。晶胞的大小和形状可用晶胞的棱边长度 a、b、c和棱边夹角α、β、γ 6 个参数来表示，其中晶胞的棱边长度称为晶格常数或点阵常数。在立方晶格中，a=b=c，α=β=γ=90°。晶胞在三维空间的重复堆积就构成了晶格，利用晶胞的结构就可以描述晶格和晶体结构。

2.1.3.2　典型金属的晶体结构

金属中由于原子间通过较强的金属键结合，原子趋于紧密排列，构成了少数几种高对称性的简单晶体结构。在金属元素中，约有 90%以上的金属晶体结构都属于下列3种晶格形式。

1．体心立方晶格

体心立方晶格也称 B.C.C.晶格（Body-Centered Cubic Lattice），如图 2.2所示。在体心立方晶格的晶胞中，立方体的8个角上各有一个原子，在立方体的中心排列一个原子。

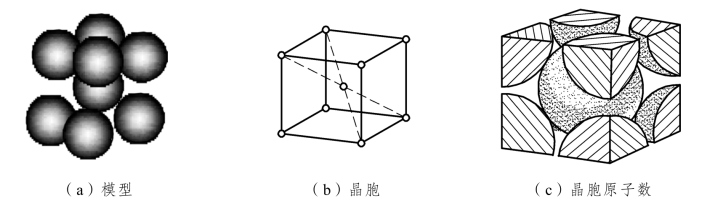
图2.2　体心立方晶胞示意图

体心立方晶格具有如下特征。

①晶格常数：。

②晶胞原子数：体心立方晶胞每个角上的原子为相邻的 8 个晶胞所共有，因此实际上每个晶胞所含原子数为（1/8×8＋1）个＝2个，如图2.2（c）所示。

③原子半径：因其体对角线方向上的原子彼此紧密排列，如图2.2（a）所示，显然体对角线长度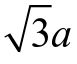等于 4 个原子半径，故体心立方晶胞的原子半径。

④配位数：晶体结构中任何一原子周围最邻近且等距离的原子数目。配位数越大，原子排列得越紧密。显然，体心立方晶格的配位数为8。

⑤致密度：晶胞中原子所占的体积与该晶胞体积之比，它也可表示晶胞中原子排列的紧密程度。体心立方晶胞中原子所占的体积为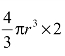，晶胞体积为a3，故其致密度为

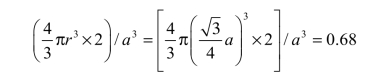
即在体心立方晶格金属中，有 68%的体积被原子所占据，其余 32%的体积为空隙。

⑥间隙半径：晶格空隙中能容纳的最大球体半径。晶胞中有两种间隙：一种是八面体间隙，如图 2.3（a）所示，其间隙半径为 0.154r；另一种是四面体间隙，如图2.3（b）所示，其半径为0.291r。

属于体心立方晶格的金属有α-Fe、Cr、Mn、Mo、W、V、Nb、β-Ti等。

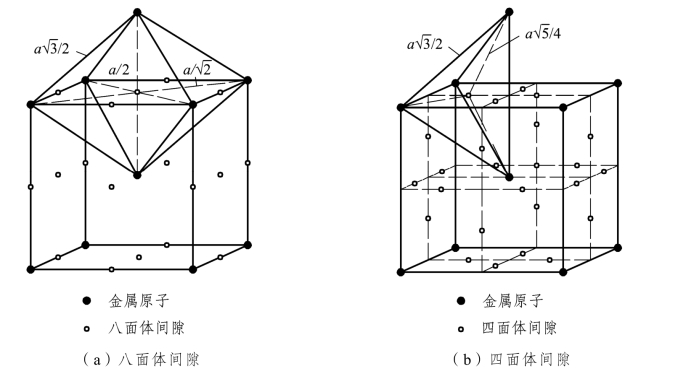
图2.3　体心立方晶格中的间隙

2．面心立方晶格

面心立方晶格也称F.C.C.晶格（Face-Centered Cubic Lattice），如图2.4所示。在晶胞8个角及6个面的中心各分布着一个原子。每个面心位置的原子同时属于两个晶胞所共有，故每个面心立方晶胞中仅包含（1/8×8＋1/2×6）个＝4 个原子。在面对角线上，面中心的原子与该面4个角上的各原子相互接触，紧密排列，其原子半径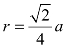，配位数为12，致密度为

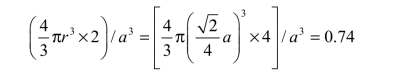
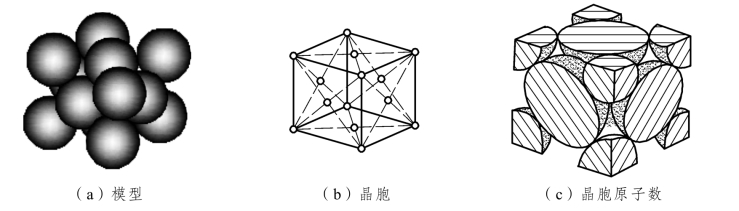
图2.4　面心立方晶胞示意图

四面体间隙半径为0.225r，八面体间隙半径为0.414r，如图2.5所示。

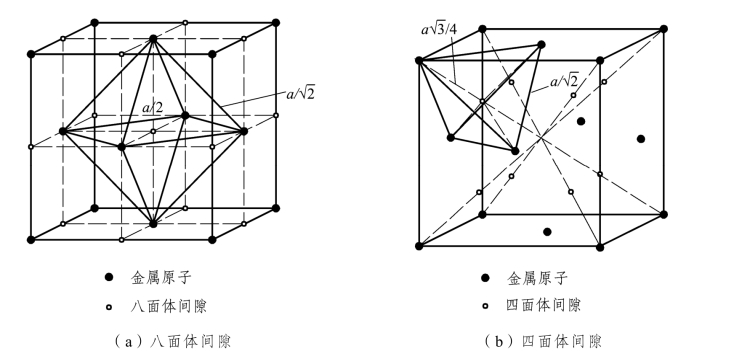
图2.5　面心立方晶格中的间隙

具有面心立方晶格的金属有γ-Fe、Al、Cu、Ni、Au、Ag、Pt、β-Co等。

3．密排六方晶格

密排六方晶格也称H.C.P.晶格（Hexagonal Close-Packed Lattice），如图2.6所示。密排六方晶格的晶胞是六方柱体，它是由6个呈长方形的侧面和2个呈六边形的底面组成的，所以要用两个晶格常数表示：上、下底面间距c和六边形的边长 a，在紧密排列情况下c/a=1.633。在密排六方晶胞中，在六方体的 12个角上和上、下底面的中心各排列着一个原子，在晶胞中间还有 3 个均匀分布的原子。每个角上的原子为相邻的 6 个晶胞所共有，上、下底面中心的原子为 2 个晶胞所共有，晶胞内部 3 个原子为该晶胞独有，所以密排六方晶胞中原子数为（12×1/6＋2×1/2＋3）个＝6 个。密排六方晶胞的原子半径为，配位数为12，致密度为0.74。四面体间隙半径为0.225r，八面体间隙半径为0.414r，如图2.7所示。

具有密排六方晶格的金属有Mg、Zn、Be、Cd、α-Co、α-Ti等。

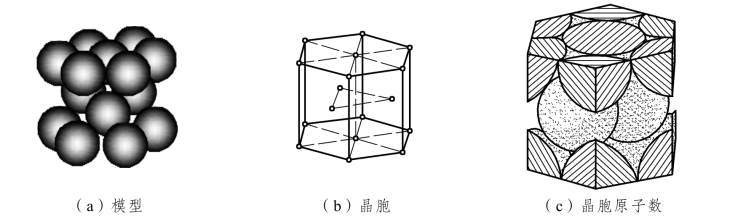
图2.6　密排六方晶胞示意图

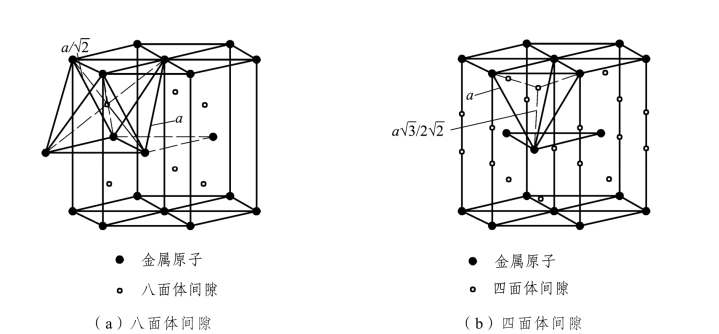
图2.7　密排六方晶格中的间隙

在晶体中，由于不同晶面和晶向上原子排列的方式和紧密程度不相同，不同方向上原子结合力的大小也就不同，所以金属晶体在不同方向上的力学、物理及化学性能也有一定的差异，此特性称为晶体的各向异性。

2.1.3.3　晶面、晶向

在晶体中，通过晶体中原子中心的平面称为晶面，任一通过晶体中原子中心的直线为原子列，其所代表的方向称为晶向。晶面和晶向可分别用晶面指数和晶向指数来表达。

1．立方晶系的晶面指数的确定方法

（1）设定一个空间坐标系，原点应在所求晶面之外。

（2）以晶格常数 a 为长度单位，写出欲定晶面在3条坐标轴上的截距，所求晶面与坐标轴平行时，截距为∞。(www.daowen.com)

（3）将所得3个截距之值变为倒数。

（4）再将这3个倒数按比例化为最小整数。

（5）将 3 个整数写在圆括号内即为晶面指数。晶面指数的一般标记为（hkl）。截距为负数时，在指数上加“－”号。

在立方晶格中，最重要的 3 种晶面是（100）、（110）、（111），如图 2.8所示。但应注意，某一晶面指数并不只代表某一具体晶面，而是代表一组相互平行的晶面，即所有相互平行的晶面都具有相同的晶面指数。

在同一种晶格中，有些晶面虽然在空间的位向不同，但其原子的排列情况完全相同，这些晶面均属于一个晶面族，其晶面指数用大括号表示，即{hkl}。例如，在立方晶胞中（100）、（010）、（001）同属一个晶面族{100}，可以表示为

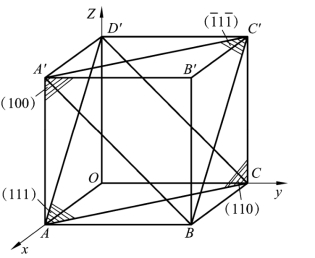
图2.8　立方晶胞中的主要晶面

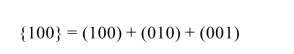
如图2.9所示。

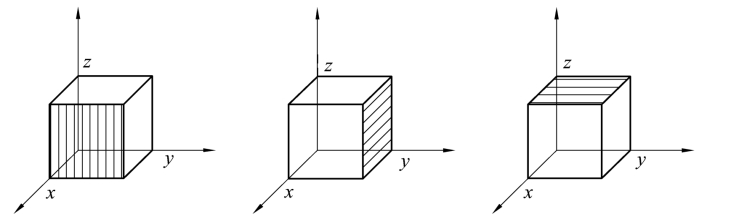
图2.9　立方晶系的{100}晶面族

同理，{110}、{111}晶面族可表示为

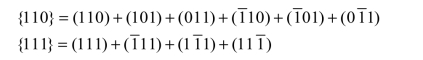
如图2.10和图2.11所示。

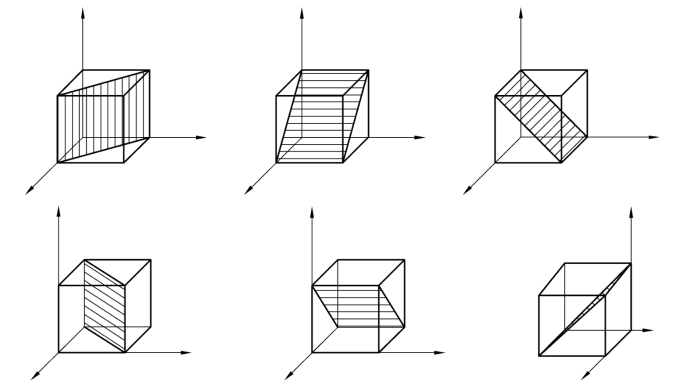
图2.10　立方晶系的{110}晶面族

2．立方晶系的晶向指数的确定方法

（1）设定一个空间坐标系，通过坐标原点引一条直线，使其平行于所求的晶向。

（2）求出该直线上任意一结点的3个坐标值。

（3）将坐标值按比例化为最小整数。

（4）将化好的整数记在方括号内即为所求的晶面指数。晶向指数的一般形式为[uvw]。坐标为负数时，在指数上加“－”号。

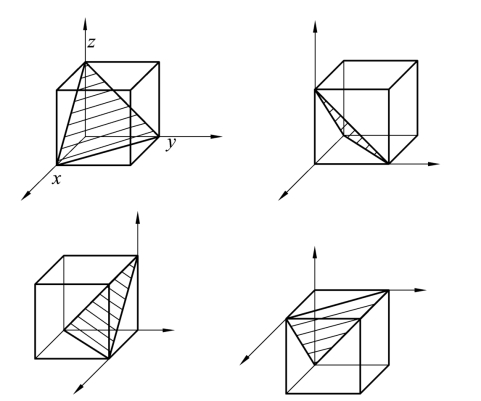
图2.11　立方晶系的{111}晶面族

立方晶格中，最重要的 3 种晶向是[100]、[110]、[111]，如图 2.12 所示。但应注意，晶向指数所表示的不仅仅是一条直线的位向，而是表示一组原子排列相同的平行晶向，即所有相互平行的晶向，都具有相同的晶向指数。

原子排列相同但空间位向不同的所有晶向称为晶向族，用<uvw>表示。例如，在立方晶胞中，[100]、[010]、[001]同属一个晶向族<100>，可表示为

<100>＝[100]＋[010]＋[001]

在立方晶系中，一个晶面指数与一个晶向指数数值和符号相同时，则该晶面与该晶向互相垂直，如（111）⊥[111]，如图2.13所示。

图2.12　立方晶胞中的主要晶向

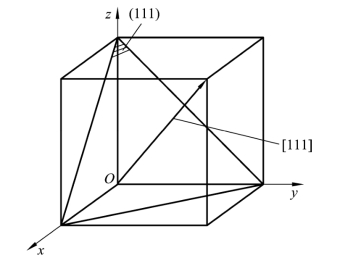
图2.13　晶面和晶向相互垂直

3．六方晶系晶面和晶向指数的确定

用上述方法确定六方晶系的晶面和晶向指数时，从其各晶面指数和晶向指数中，却反映不出原子排列情况相同而空间位向不同的各等同晶面和各等同晶向之间的关系。

六方晶系采用四指数法表示晶面和晶向。水平坐标轴选用相互成 120°夹角的三坐标轴 a1，a2，a3，再加上垂直轴 c，构成 4 个坐标轴系。这样确定出的六方晶系的晶面和晶向指数，就能较好地反映出各原子排列情况相同，而空间位向不同的各等同晶面和晶向之间的关系。这时可用（hkil）表示晶面指数，用[uvtw]表示晶向指数。由于在二维平面最多只有两个独立的坐标，存在下列关系：

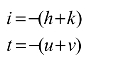
用 4 个坐标轴确定六方晶系的晶面指数的方法，与用 3 个坐标轴时相同，只需多确定出在 a3轴上的截距。它也可以先用 3 个坐标确定，再根据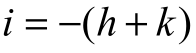的关系，加上第 4 个指数。而用4个坐标轴确定晶向指数时，必须从坐标原点出发，沿平行于 4 个坐标轴的方向依次移动，最后到达所求晶向上的某一结点，并应满足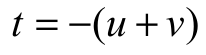。六方晶系的几个主要晶面和晶向如图2.14所示。

图2.14　六方晶系的几个主要晶面和晶向

在密排六方晶格中，原子密度最大的晶面族为{0001}，称为密排面；原子密度最大的晶向族为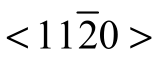，称为密排方向。

4．密排面和密排方向

不同晶体结构中不同晶面、不同晶向上原子的排列方式和排列密度不一样。晶面上原子排列的紧密程度，可用晶面的原子密度（单位面积上的原子数）表示；晶向上原子排列的紧密程度，可用晶向的原子密度（单位长度上的原子数）表示。原子密度最大的晶面称为密排面，原子密度最大的晶向称为密排方向。由表 2.1 和表 2.2 说明，在体心立方晶格中，密排面为{110}，密排方向为<111>，而面心立方晶格中，密排面为{111}，密排方向为<110>。由于不同晶面和晶向上原子排列的方式和密度不同，它们之间的结合力的大小也不相同，因而金属晶体不同方向上的性能不同。这种性质叫作晶体的各向异性。非晶体在各个方向上性能完全相同，这种性质叫作非晶体的各向同性。

表2.1　体心立方、面心立方晶格主要晶面的原子排列和密度

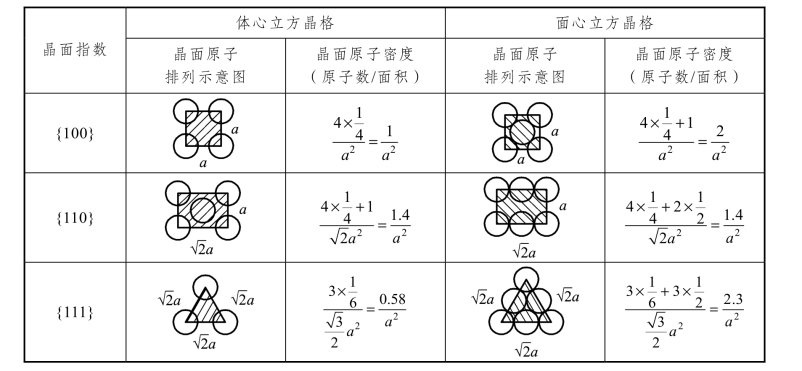
表2.2　体心立方、面心立方晶格主要晶向的原子排列和密度