根据上述,由于均衡供用电,可以减小负荷峰谷差,改善负荷特征系数,因此可以计算出:在线路总损耗中,可变损耗所占比例不同的线路,在不同的负荷曲线特征系数下的降损效果,计算式为
![]()
式中 λ——可变损耗在线路总损耗中所占的比重;
K1、K2——改善前、后线路负荷曲线特征系数;
Δ(ΔA∑)%——线路总损耗降低的百分数。
根据式(4-23),当假设式中各量为相应值时,即可得到下面的改善线路负荷曲线特征系数之不同情况下的降损效果。
表4-3 在不同的λ值下,将K1改善为K2时,降损效果Δ(ΔA)%表

表4-3中的数字为线路线损(线损电量或线损率)降低的百分数。从表4-3中可以看出,当采取措施,改善负荷曲线特征系数时,降低线损的效果是显著的,并且曲线的改善程度愈大,降低线损的效果也愈大。而且对于可变损耗所占比重愈大的线路,降低线损的效果也愈大。例如,对一条可变损耗占70%的重负荷线路,在用电和供电不太均衡,负荷起伏波动较大,有一条劣负荷曲线,其特征系数K1=1.25(相当于线路负荷率f1=27%左右,请参见图4-12所示曲线)的初始情况下,经采取相应措施,使负荷曲线有所改善,其特征系数降至K2=1.10(相当于线路负荷率f2=48%左右),则可使线路的总线损电量和总线损率均降低15.79%。如进一步采取相应措施,使负荷曲线进一步优化,其特征系数再降低至K3=1.05(相当于线路负荷率f3=66%左右),则可使线路的总线损电量和总线损率均比采取措施前降低20.61%。降损效果相当显著。
由于人们对线路负荷率F的认识和应用比线路负荷曲线特征系数K要早和普遍,因此,在计算确定本措施降损效果之前,对图4-13特作简要说明。在同一线路的不同两日中,若线路平均负荷电流Ipj值相同(或接近相同),而线路负荷愈不均衡,则说明当日线路中的最大负荷电流Izd值愈大,线路负荷率F愈低,这是因为F∝1/Izd,同时,线路负荷愈不均衡,则又说明当日线路负荷曲线特征系数K值愈大,所以,在线路负荷愈不均衡的情况下,F∝1/K,曲线F=f(K)呈图中所示状态,即K值愈优化(愈接近1.0),F值升高愈陡急。并且,在线路供电量一定的情况下,负荷系数K值愈大,则因线路中可变损耗电量ΔAkb∝K2,ΔAkb值亦更大;而ΔAkb值愈大,则可变损耗电量在线路总损耗电量中所占比例λ值亦愈大。
 (https://www.daowen.com)
(https://www.daowen.com)
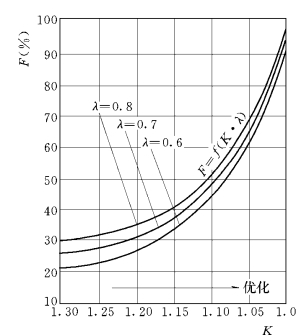
图4-13 线路负荷率F与线路负荷曲线特征系数K、可变损耗比例系数λ之关系曲线示意图
从图4-13中可见,线路在同一负荷率F值下,λ值大者,K值亦为大;反之,λ值小者,K值亦为小。这说明λ值较大的线路对改善优化负荷K值所获取的降损效果优于λ值较小的线路。比如,将K1=1.25(相当于f=23%~32%)改善优化为K2=1.10时,对于λ=0.8(对应于f≈52%)的线路,降损效果可达18.05%,而对于λ=0.7(对应于f≈48%)的线路只有15.79%,对于λ=0.6(对应于f≈44%)的线路只有13.54%(见表4-3)。另外,λ值愈大的线路,受cosφ值的影响亦愈大,因此,曲线F=f(K·cosφ)与曲线F=f(K·λ)类似。
在了解表4-3中改善负荷曲线特征系数时线路总损耗降低的百分数后,即可计算出λ=0.2~0.8中任何一条线路的总损耗的降低量,即线路总线损电量的节约量。计算式为
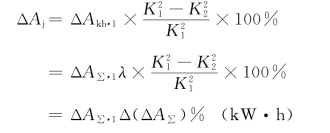
式中 ΔAj——线路总线损的节约量,kW·h;
ΔAkb·1——改善负荷曲线特征系数前的线路可变损耗,kW·h;
ΔA∑·1——改善负荷曲线特征系数前的线路总损耗,kW·h。
须指出的是,负荷曲线特征系数K1与K2、可变损耗比重λ、线路总损耗ΔA∑·1的计算确定方法在前面相关章节中已做了叙述,请翻阅。
【例4-1】 当对图4-13中的35kV输电线路的电力负荷采取相应调整措施,使原负荷曲线特征系数K1=1.05,改善为K2=1.03(相当于将线路负荷率提高到f2≈78%左右)时,试计算出该线路的线损节约量和理论线损率降低后之值。
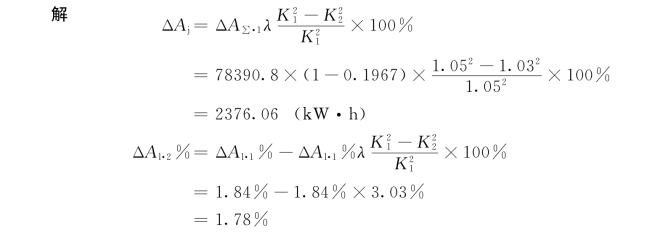
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




