1.PID调节原理

PID调节器就是根据系统的误差，按偏差的比例（P）、积分（I）和微分（D）进行控制，是过程控制领域中应用最为广泛的一种自动控制器。当被控对象的结构和参数不能完全掌握，或得不到精确的数学模型时，或控制理论的其他技术难以采用时，系统控制器的结构和参数必须依靠经验和现场调试来确定，这时应用PID控制技术最为方便。

PID控制，实际中也有PI和PD控制，在理论上可以证明，对于过程控制的典型对象——“一阶滞后+纯滞后”与“二阶滞后+纯滞后”的控制对象，PID控制器是一种最优控制。PID调节规律是连续系统动态品质校正的一种有效方法，它的参数整定方式简便，结构改变灵活。

连续系统PID调节器为对误差的比例、积分和微分控制，即

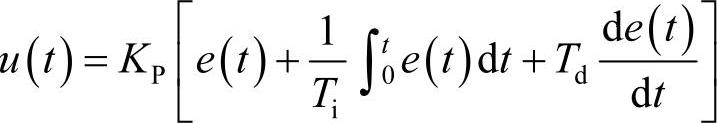
或

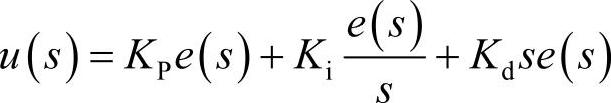
式中，T_i、T_d分别为积分和微分时间常数；K_p、K_i、K_d分别为比例系数、积分系数、微分系数。

2.PID运算指令工作原理

PID运算指令是将从输入通道获取指定的二进制数据的输入范围，按照设定参数进行PID运算，并将运算结果存放到输出通道中。其梯形图符号如下：

在CP1H PLC中操作数可选取的存储器区域如下：

S：CIO，W，H，A，T，C，D，*D、@D或DR。

C：CIO 0000～CIO 6105，W000～W473，H000～H473，A000～A921，T0000～T4057，C0000～C4057，D00000～D32729，*D或@D。

D：CIO，W，H，A，T，C，D，*D、@D或DR。

PID指令的参数通道范围是同一数据区中的C～C+38，参数通道的分配见表8-4。PID指令各参数的具体含义见表8-5。

表8-4 通道C～C+38PID参数表

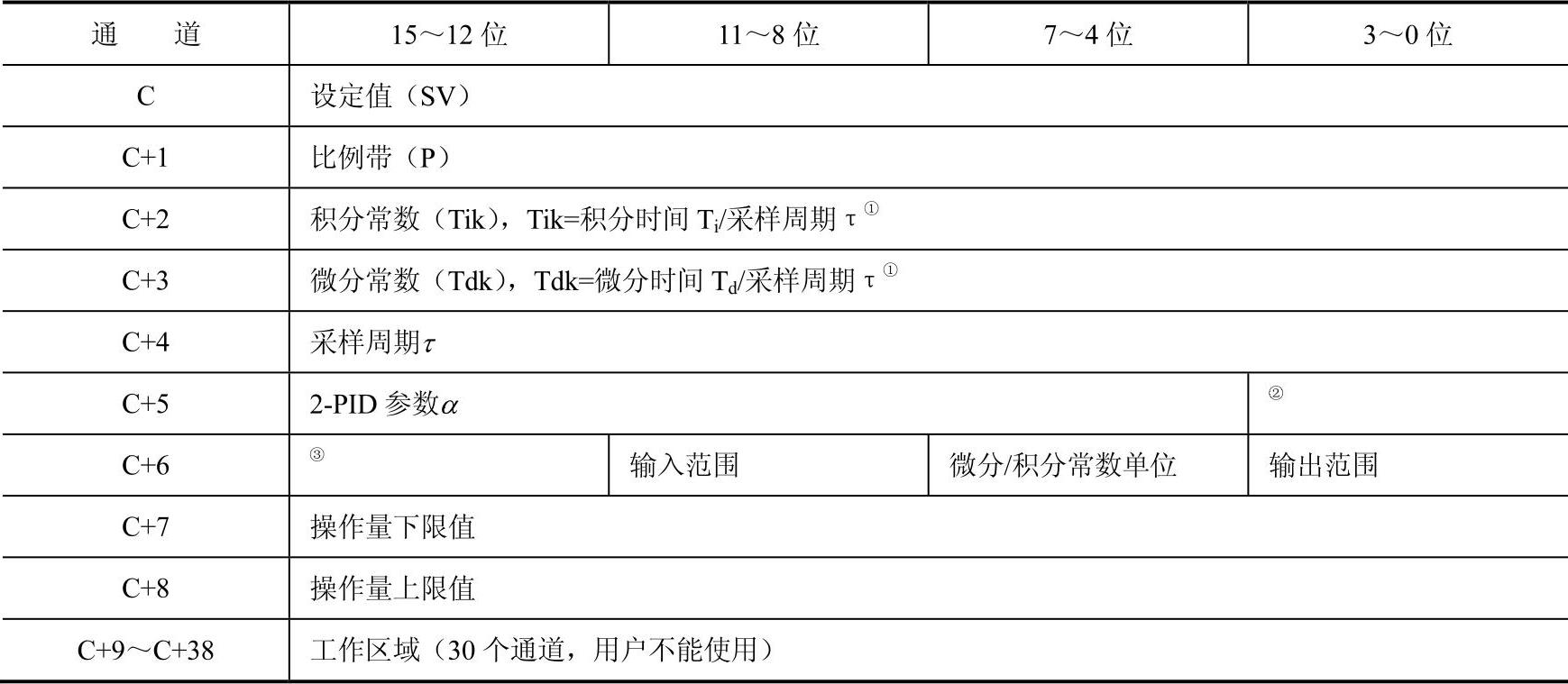
①C+2和C+3通道中设定的值除以C+6中设定的微分/积分常数单位可得实际的微分/积分时间。

②C+5通道的0位：设定PID的正/反作用。

C+5通道的1位：设定PID常数的作用时间。

C+5通道的2位：保持为0。

C+5通道的3位：设定PID运算操作量的输出值。

③C+6通道的12位：设定是否对PID运算的操作量设置限值。

C+6通道的13～15位：保持0。

PID指令的工作原理是在执行条件为ON的上升沿，根据设定的PID参数，工作区域（C+9～C+38通道）被初始化，PID运算开始，在刚开始运行时为避免控制系统受反向冲击（无冲击运行），运算输出值不发生突变和大幅变化。当PID参数更改时，指令执行条件从OFF变为ON，更改参数才开始有效。

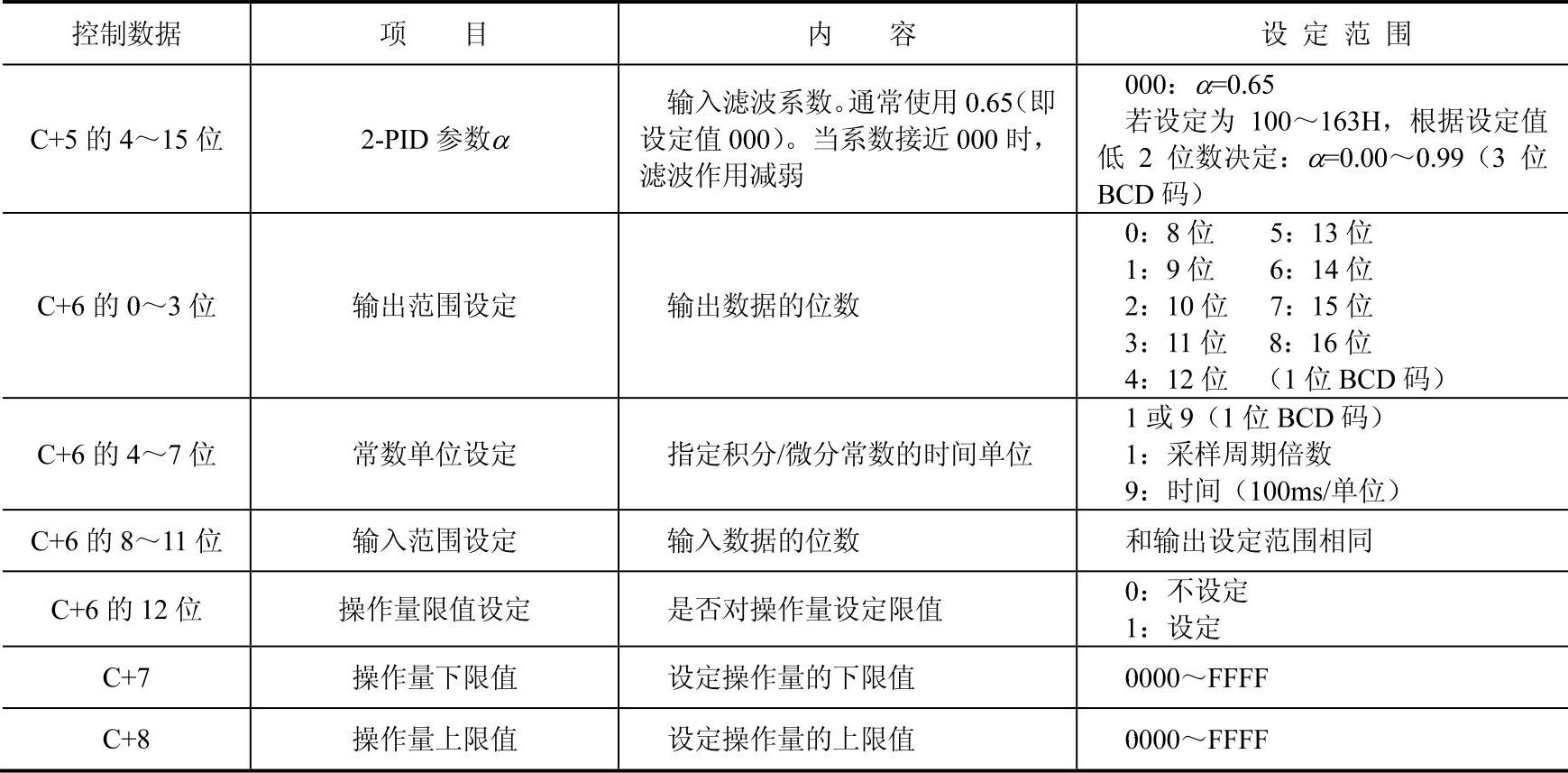
表8-5 PID参数设置表

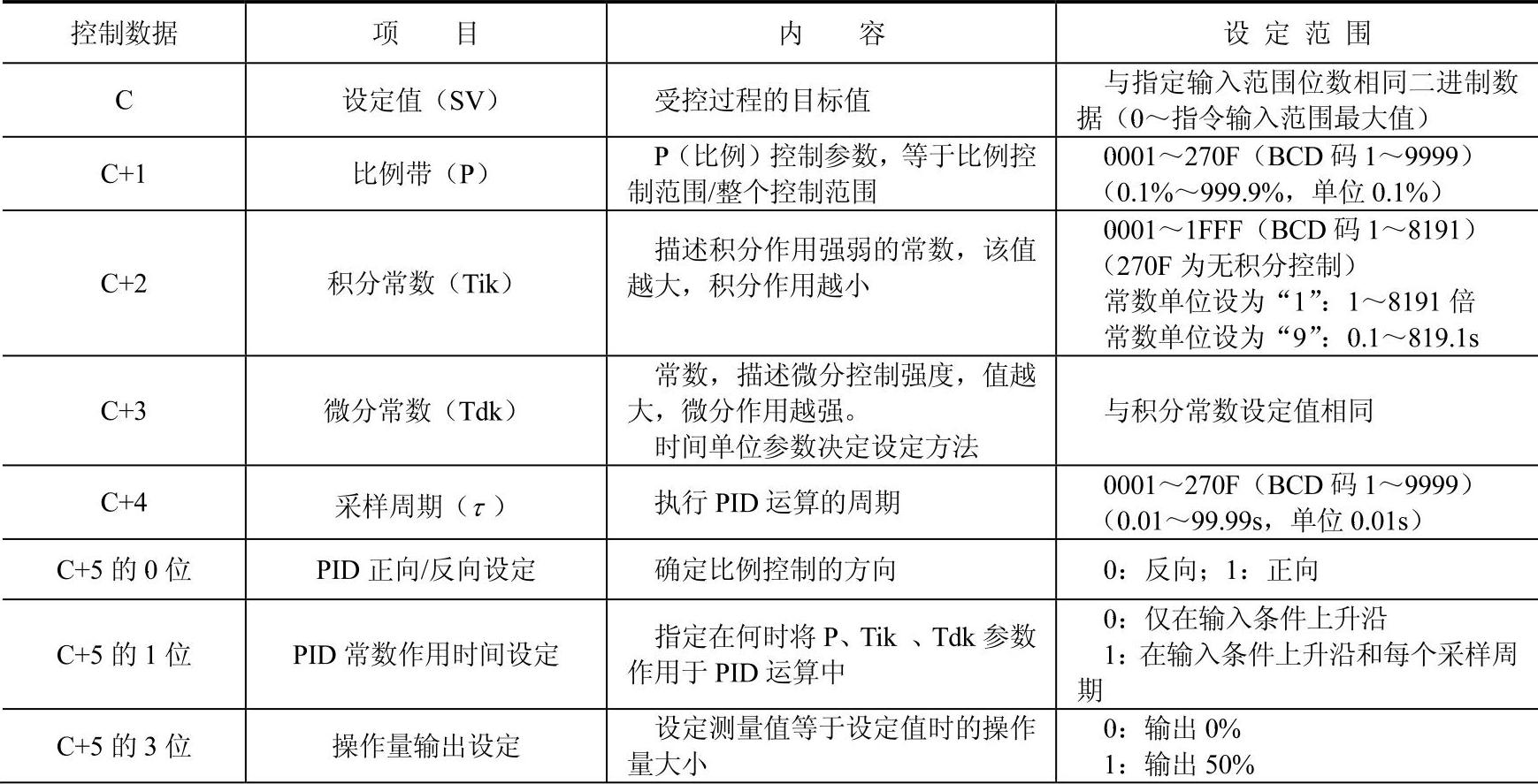(www.daowen.com)

（续）

在指令执行条件为ON时，PID运算是按采样周期间隔执行的，采样周期是采集测量数据提供给PID运算的间隔时间。该采样周期的设置由PID参数决定。但是，PID指令是根据CPU的扫描周期执行的，所以可能会出现超过采样周期的情况，例如，采样周期为100ms，扫描周期为150ms，此时PID指令将150ms执行一次，而不是按采样周期的100ms执行一次。但是当采样周期大于扫描周期时，假设采样周期为100ms，扫描周期为60ms时，PID指令的执行情况如图8-38所示。

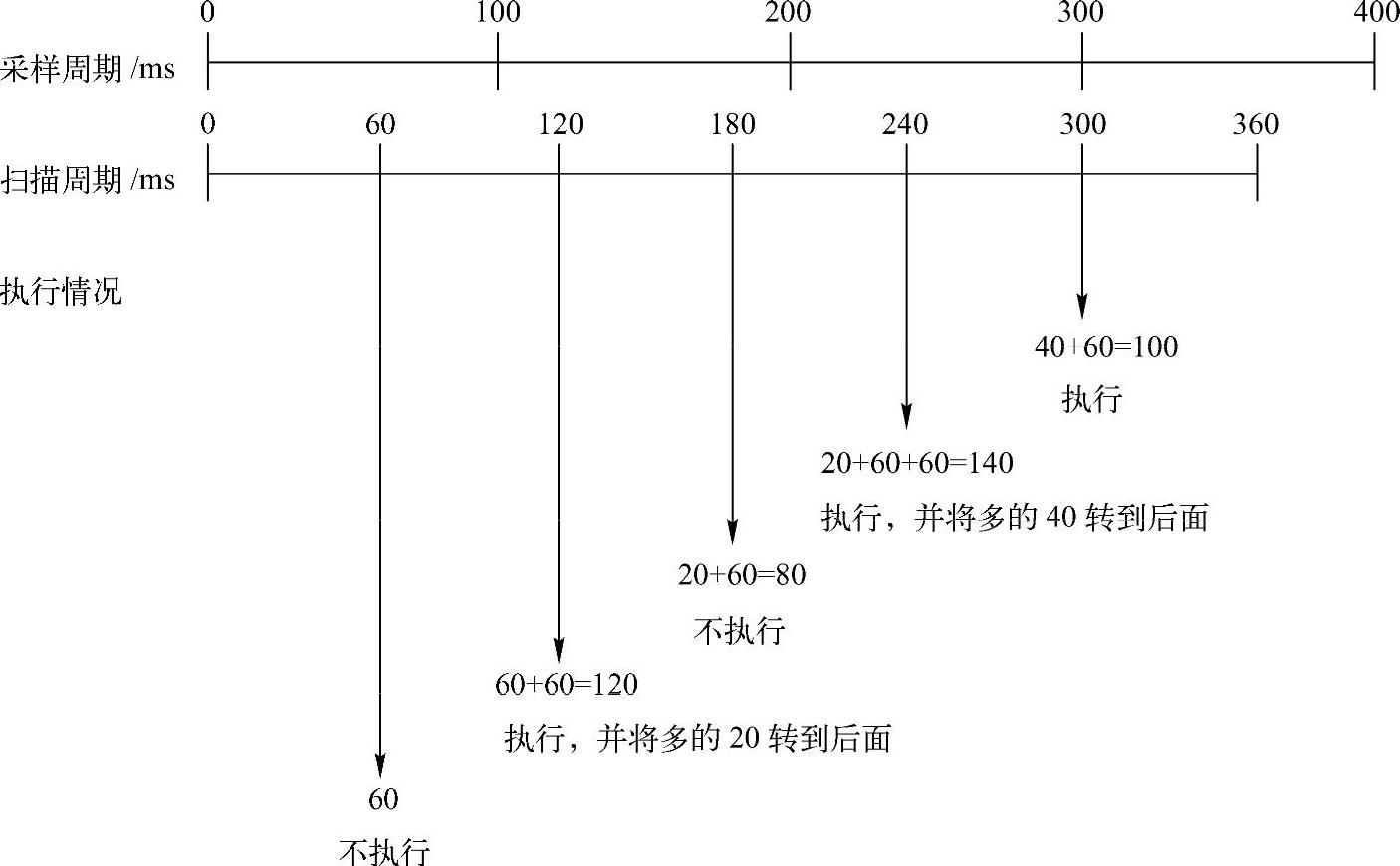
图8-38 采样周期与扫描周期关系图

从图8-38可以看出，PID指令是在每个扫描周期（即每隔60ms）进行一次指令是否执行的判断：第1个扫描周期60ms小于100ms，故指令不执行；第2个扫描周期60ms+60ms=120ms大于100ms，故指令执行，并将多余的20ms转入下一周期；第3个扫描周期20ms+60ms=80ms小于100ms，故指令不执行，并将这多余的80ms转入下一周期；第4个扫描周期80ms+60ms=140ms大于100ms，故指令执行，并将多余的40ms转入下一周期；第5个扫描周期40ms+60ms=100ms，故指令执行。以后依次循环。

通过以上分析不难发现，在前300ms中指令执行分别是在120ms、240ms、300ms处，它们是扫描周期的整数倍而不是采样周期的整数倍。因此当采样周期设置较长时，可以不考虑扫描周期与采样周期的关系。

使用PID指令时需要注意以下几点：

1）PID参数SV（设定值）超出数据区范围；实际的采样周期超过设定的采样周期2倍时，P_ER置位。但不影响PID运算。

2）PID运算正在执行时，P_CY置位。

3）PID运算的操作量大于设定操作量上限值时，大于标志P_GT置位，并以操作量上限值输出。

4）PID运算的操作量小于设定操作量下限值时，小于标志P_LT置位，并以操作量下限值输出。

5）在中断程序，子程序，IL和ILC之间，JMP和JME之间，以及使用了STEP和SNXT的步进程序中，禁止使用PID指令。

6）PID控制运算过程中，当指令执行条件为OFF时，所有设定值保持不变，通过把操作量写入输出字，可以进行手动控制。

3.二自由度PID控制算法原理

CP1H PLC指令系统中的PID指令算法采用的是二自由度PID控制算法（以下简称2-PID指令）该控制算法的传递函数功能图如图8-39所示。

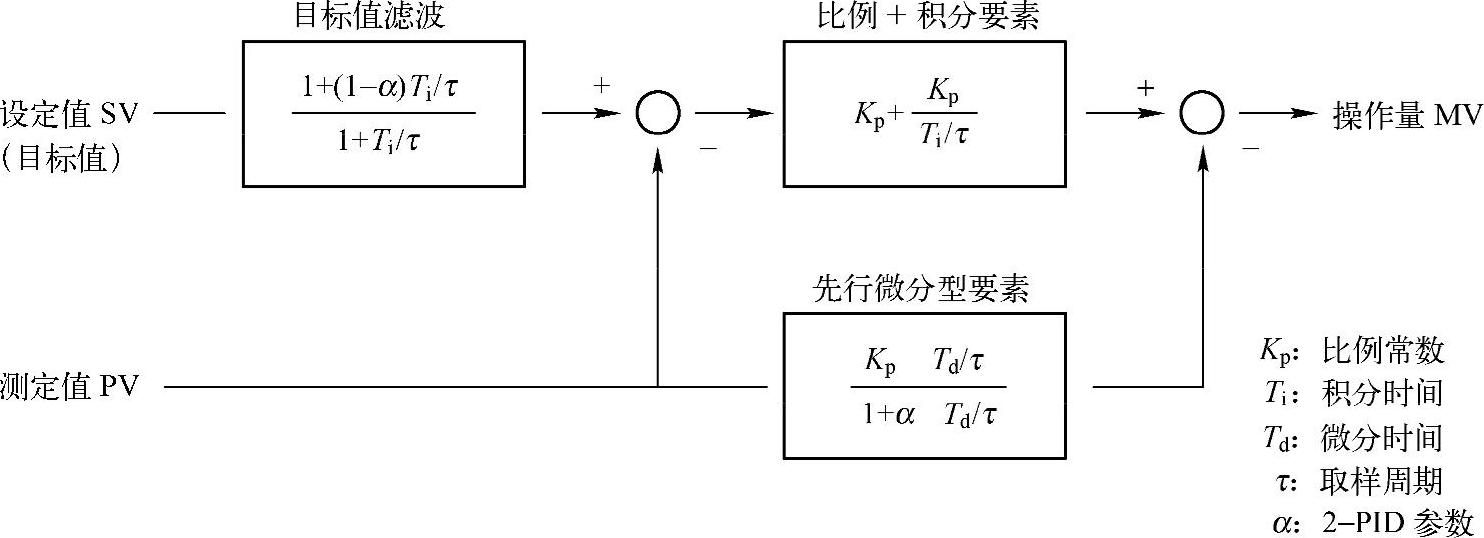
图8-39 2-PID控制算法传递函数功能图

从图8-39可以看出所谓2-PID控制算法实际上是设定值带一阶滤波器并采用微分先行的不完全微分的PID控制算法，与普通PID相比，它具有以下两个特点：

1）设定值前面加了一个目标滤波器，该滤波器是一个以α为可变参数的滤波器，该滤波器有以下两个作用：

①具有低通滤波的作用。α值的取值范围是0～1，当α值逐渐增大时，滤波器的低通滤波特性将越来越强；当α=1时，目标滤波器的传递函数变成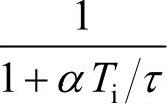，这是一个典型的一阶惯性环节，众所周知，一阶惯性环节是一个典型的低通滤波器。

②具有抑制超调的作用。随着α值变大，其抑制超调的作用将越来越明显。

2）二自由度控制算法的另一特点是其微分环节采用了不完全微分的微分先行算法。所谓不完全微分是指在微分环节T_d/τ中加了一个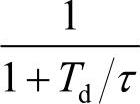的低通滤波器。微分信号的引入可以改善系统的动态特性，但可能会引入高频干扰，加入了一阶惯性环节后可有效抑制高频干扰。

普通微分环节对阶跃信号的响应是一个幅值很高而宽度很窄的脉冲，它对系统会造成较强的冲击且微分持续的时间很短；不完全微分环节对阶跃信号的响应是开始时幅值较高然后很快衰减，与普通微分环节相比，幅值较低而持续时间较长。显然不完全微分环节特性要优于普通微分环节特性，因此目前在工程实践中已很少使用普通微分环节而更多地使用不完全微分环节。

图8-39中，α值越小其特性就越接近普通微分环节，当α系数设为0时，就等同于普通微分环节，因此在参数整定时，若使用不完全微分则α系数设为0～1的非0值。

另外，微分环节采用了微分先行的方式，从图8-39可看出，微分环节只对操作量进行微分而不对给定值微分，其优点是当给定值变化时（给定值变化通常会比较剧烈），由于没有微分可以避免系统可能产生的振荡；而当操作量发生变化时（输出变化通常比较缓和），由于加入微分可以缩短过渡过程，从而改善系统动态响应。

综上所述，2-PID控制算法的核心是其对给定值的响应和对扰动的响应采用了不同的控制算法，这也是“二自由度”名称的由来。对于给定值，控制算法是一个目标滤波器加PI算法，这样可以有效抑制超调；对于扰动，控制算法是一个采用了不完全微分的PID算法，这样可以有效地改善系统动态响应。