正等轴测图常用的作图方法有坐标法、叠加法和切割法。其中，坐标法是最基本的作图方法。

（1）坐标法

坐标法是根据平面立体上各顶点坐标，分别画出其轴测投影，然后依次连接各顶点，从而完成立体的轴测图。

【例5.1】　作出如图5.6 正六棱柱的正等轴测图。

分析：首先，在形体的投影图上建立坐标系（O-XYZ），使形体上的棱线（棱面）尽量与轴测轴（轴测坐标面）平行；再运用平行投影特性求出形体上各顶点、棱线、棱面的轴测投影；最后判断可见性，去掉不可见的虚线，即得形体的轴测图。

如图5.6 所示的正六棱柱上下底面都为水平面（平行于XOY），且为对称图形，棱线为铅垂线（平行于OZ 轴），因此，选择直角坐标系时，直角坐标轴可按对称位置选取，坐标原点设在上底面中心，则六棱柱上底面的顶点A、D 在OX 轴上，边线BC、EF 平行于OX 轴，各棱线平行于OZ 轴。

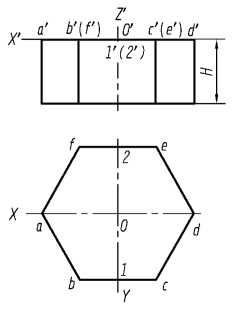
图5.6　正六棱柱的三视图

画正六棱柱的正等轴测图时，根据轴测投影特性，先确定A1、D1 点，B1C1、E1F1 边，再画出各棱线，最后连接下底面各可见顶点。

图5.7　正六棱柱的正等测的画法

作图过程：

①作轴测轴，并在其上量取A1、D1、11、21 点，如图5.7（a）所示。

②过11、21 点分别作X1 轴的平行线，量得B1、C1、E1、F1 点，连成顶面，如图5.7（b）所示。(www.daowen.com)

③由F1、A1、B1、C1 沿Z1 轴量取H，得F2、A2、B2、C2，连接F2、A2、B2、C2，如图5.7（c）所示。

④物体上不可见轮廓不画，加粗可见轮廓线，得到如图5.7（d）所示的结果。

（2）切割法

对不完整的切口体，先按完整形体画出，然后用切割的方法逐一切去多余部分，画出剩余的不完整部分，称为切割法。

【例5.2】　如图5.8（a）所示，根据不完整切口体的三视图，画出它的正等轴测图。

分析：该物体可采用坐标法结合切割法作图，即将该物体看成由一个长方体切割而成。左上角被一个正垂面切割，左方的前后分别被一个铅垂面切割掉一个三棱柱。铅垂面截切后与正垂面相交产生与三根坐标轴均不平行的线段，在轴测图上不能直接从正投影图中量取，必须按坐标求出其端点，然后连接各点。

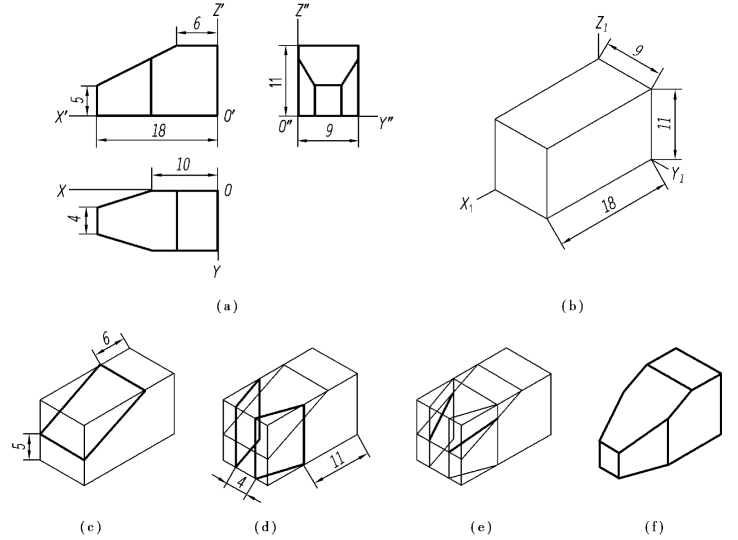
图5.8　用切割法作立体正等测的画法

作图过程：

①作轴测轴，按尺寸18、9、11 作出长方体的正等测，如图5.8（b）所示。

②根据尺寸5 和6 画出长方体左上角被正垂面切割后的正等测，如图5.8（c）所示。

③再根据尺寸4 和11 画出长方体左方的前后分别被一个铅垂面切割掉一个三棱柱后的正等测，如图5.8（d）所示。

④画出铅垂面与正垂面相交产生的交线。与三根坐标轴均不平行，在轴测图上不能直接从三视图中量取，必须按坐标求出其交点，然后连接两端点，如图5.8（e）所示。

⑤擦去作图线，加深，得到如图5.8（f）所示的结果。