平面与平面立体相交的截交线是由直线段组成的封闭多边形，多边形的顶点是截平面与立体棱线（或底边）的交点，多边形的各边是截平面与立体棱面或底面的交线。因此，求平面立体的截交线可以归结为求两平面的交线和求棱线与截平面的交点的问题。

下面主要以特殊位置截平面为例来说明平面立体截交线的求解方法和步骤。

【例3.6】　如图3.15（a）所示，补全三棱锥被平面P 截切后的投影。

分析：由图3.15（a）知，正垂面P 与三棱锥的侧面SAB、SBC 和SAC 分别相交于直线段ⅠⅡ、ⅡⅢ和ⅠⅢ。另外，Ⅰ、Ⅱ、Ⅲ点分别位于棱线SA、SB 和SC 上，可根据直线上点的投影特性求出其三面投影。

作图：具体作法如图3.15（b）所示。

①直接求出P 平面与三棱锥棱线交点的正面投影1′、2′、3′。

②根据直线上点的投影规律，分别求出各点的水平投影1、2、3 和侧面投影1″、2″、3″。

③顺次连接各点的同面投影，判断可见性，即得截交线的投影。

④整理棱线，完成作图，如图3.15（c）所示。(www.daowen.com)

【例3.7】　如图3.16（a）所示，五棱柱被一正垂面P 切割，求截交线及五棱柱被切割后的三面投影。

分析：由图3.16（a）可知，截平面P 与五棱柱的四个棱面和上底面相交，截交线为五边形。五边形的顶点A、B、C、D、E 分别是两条底边、三条棱线与截平面P 的交点。由于截平面P 是正垂面，它的正面投影积聚为一条直线，截交线的正面投影积聚为直线段，可直接求出；然后根据A、B、C、D、E 属于五棱柱的底边和棱线，求出侧面投影和水平投影；最后顺次连接各点，即可求得截交线。

作图：具体作法如图3.16（b）所示。

①直接作出正面投影a′、b′、c′、d′、e′和水平投影a、b、c、d、e。

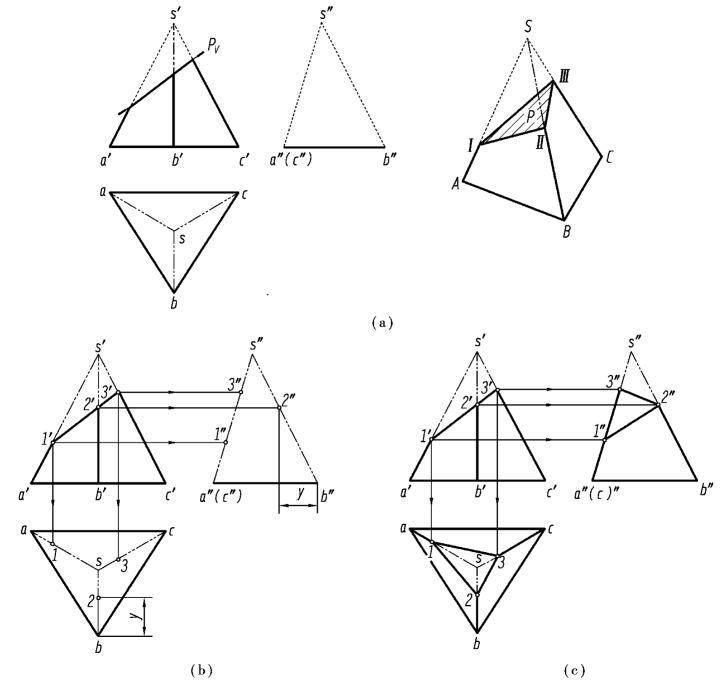
图3.15　求棱锥的截交线

②根据直线上点的投影规律，求出各点的侧面投影a″、b″、c″、d″、e″。

③依次连接五个交点的同面投影，并判断可见性。

④整理棱线，完成作图，如图3.16（c）所示。