空间两直线的相对位置关系有三种情况：平行、相交和交叉。

（1）两直线平行

空间两条直线平行，则它们的同面投影必定相互平行，如图2.16（a）、（b）所示；反之，如果两条直线的各个同面投影相互平行，则两条直线空间也一定平行。

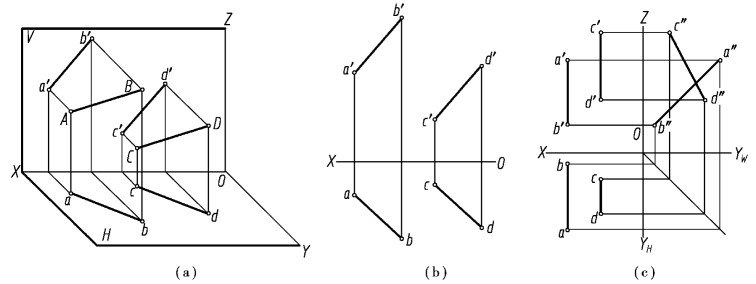
图2.16　两直线平行

要从投影图上判断两一般位置直线是否平行，只需判断它们的两个同面投影是否平行即可。若两条直线均为投影面的平行线，则要根据直线所平行的投影面上的投影是否平行来判断它们空间是否平行，如图2.16（c）。

（2）两直线相交

当两直线相交时，它们在各投影面上的同面投影必然相交，并且交点符合点的投影规律，反之亦然。

如图2.17 所示，直线AB 与CD 相交于点K，则a′b′与c′d′、ab 与cd 也必然相交，并且交点k 与k′的投影连线必然垂直于OX 轴。一般情况下，如果两条直线的两面投影都相交，且投影的交点符合空间一点的投影规律，则空间两条直线相交。但若两条直线中有一条直线为投影面的平行线时，则两组同面投影中必须包含直线所平行的投影面上的投影。

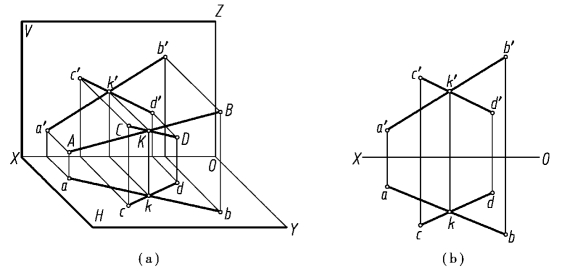
图2.17　两直线相交

（3）两直线交叉

当空间两条直线既不平行又不相交时，则称两条直线交叉。交叉两条直线的同面投影也可能相交，但各个投影的交点不符合投影规律。

如图2.18 所示，交叉两条直线同面投影的交点，实际上是两条直线上两点的重影点，其可见性可从另一投影中用前遮后、上遮下、左遮右的原则来判断。在图2.18 中，点Ⅰ和点Ⅱ是对H 面的一对重影点，点Ⅰ在直线AB 上，点Ⅱ在直线CD 上，由于z1 ＞z2，因此，从上向下投射时点Ⅰ可见，点Ⅱ不可见；同理，点Ⅲ和点Ⅳ是对V 面的一对重影点，点Ⅲ在直线CD 上，点Ⅳ在直线AB 上，由于y3 ＞y4，因此，从前向后投射时点Ⅲ可见，点Ⅳ不可见。

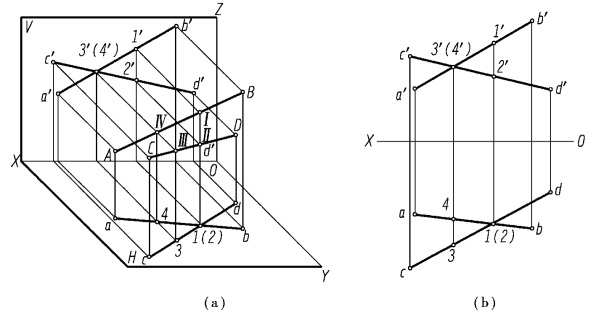
图2.18　两直线交叉(www.daowen.com)

【例2.6】　如图2.19（a）所示，点K 是两条直线AB 和CD 的交点，根据题给条件求作直线AB 的正面投影。

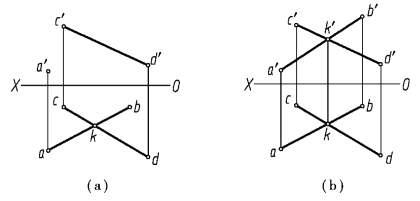
图2.19　求作直线的投影

分析：交点为两条直线的共有点，且符合点的投影规律，由此可求得交点的正面投影k′；由于B、K、A 位于同一条直线上，可求得B 点的正面投影b′。

作图：作图过程如图2.19（b）所示。

①过k 作OX 轴的垂线，与直线CD 的正面投影c′d′相交，交点即为k′。

②连接a′k′并延长，与过b 点作OX 轴的垂线相交，交点即为b′，连接a′b′，完成作图。

【例2.7】　如图2.20（a）所示，已知直线AB 和CD 的两面投影，以及点E 的水平投影e，求作直线EF 与CD 平行，并与AB 相交于点F。

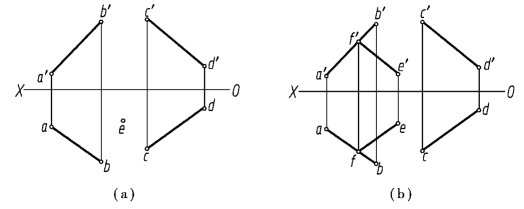
图2.20　求作直线与一直线平行且与另一直线相交

分析：两条直线平行，则它们的同面投影必定相互平行；两直线相交，则它们的同面投影必然相交，并且交点符合点的投影规律。由于已知点的水平投影e，因此，在水平投影面上过e 点作cd 的平行线，与另一条直线的水平投影ab 相交，交点即为所求点F 的水平投影f。

由于交点F 还位于直线AB 的正面投影上，按照点的投影规律，即可求出交点F 的正面投影f′；同理，求出e′，分别连接e′f′和ef，即可完成作图。

作图：作图过程如图2.20（b）所示。

①在水平投影面上过e 点作直线CD 水平投影cd 的平行线，与直线AB 的水平投影ab 相交，交点即为f。

②过f 点作OX 轴的垂线，与直线AB 的正面投影a′b′相交，交点即为f′。

③过f′作直线CD 正面投影c′d′的平行线，与过E 点的水平投影e 作OX 轴的垂线相交，交点即为E 点的正面投影e′，分别连接e′f′和ef，完成作图。