直线按照相对于投影面的位置分为三类：投影面平行线、投影面垂直线和一般位置直线。前两类又称为特殊位置直线。

直线与水平投影面、正面投影面、侧面投影面的夹角，分别称为该直线对投影面的倾角，用“α”“β”和“γ”表示，如图2.12（a）所示。

（1）投影面平行线

平行于一个投影面，而与另外两个投影面倾斜的直线，称为投影面的平行线。根据所平行的投影面不同，平行线分为正平线、水平线和侧平线。

①正平线：平行于V 面，倾斜于H、W 面的直线。

②水平线：平行于H 面，倾斜于V、W 面的直线。

③侧平线：平行于W 面，倾斜于V、H 面的直线。

表2.1 列出了正平线、水平线、侧平线的投影及其投影特性。

表2.1　投影面平行线的投影特性

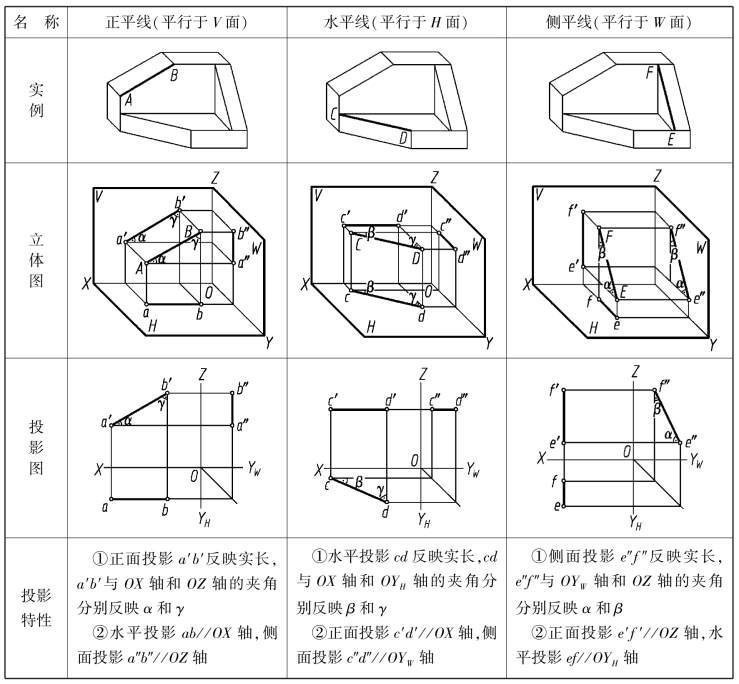
从表2.1 中可概括出投影面平行线的投影特性：

①在平行于该投影面上的投影反映实长，它与投影轴的夹角，分别反映直线对另外两个投影面的倾角。

②在另外两个投影面上的投影，分别平行于相应的投影轴。

（2）投影面垂直线

垂直于一个投影面，而与另外两个投影面平行的直线，称为投影面的垂直线。根据所垂直的投影面不同，垂直线分为正垂线、铅垂线和侧垂线。

①正垂线：垂直于V 面，平行于H、W 面的直线。

②铅垂线：垂直于H 面，平行于V、W 面的直线。

③侧垂线：垂直于W 面，平行于V、H 面的直线。

表2.2 列出了正垂线、铅垂线、侧垂线的投影及其投影特性。(www.daowen.com)

表2.2　投影面垂直线的投影特性

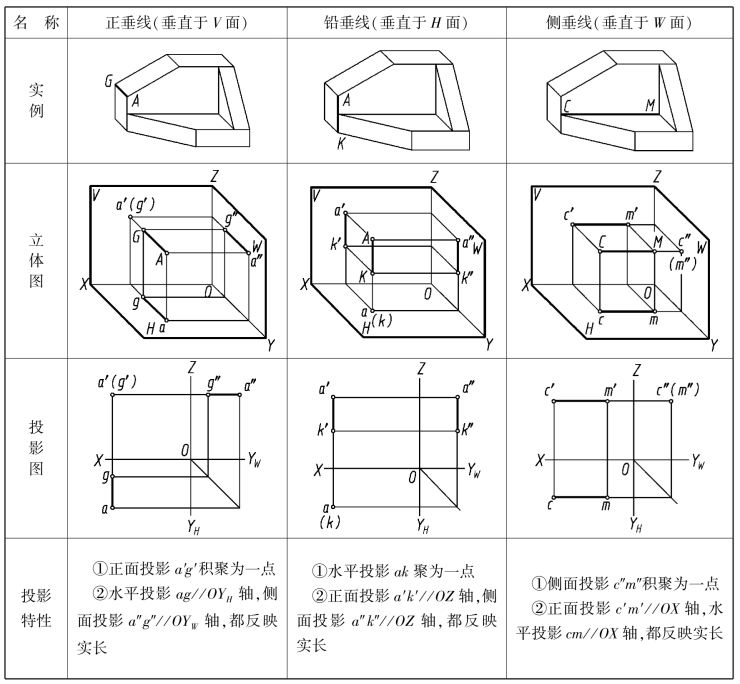
从表2.2 中可概括出投影面垂直线的投影特性：

①与直线垂直的投影面上的投影积聚为一点。

②在另两个投影面上的投影，平行于同一投影轴，并且反映实长。

（3）一般位置直线

与三个投影面都倾斜的直线称为一般位置直线。如图2.12 所示，直线的实长、投影长度和倾角之间的关系为：

ab=AB cos α，　a′b′=AB cos β，　a″b″=AB cos γ

一般位置直线的投影特性为：

①三个投影都与投影轴倾斜，其投影长度均小于实长。

②三个投影与投影轴的夹角都不反映直线对投影面的倾角。

【例2.4】　如图2.13（a）所示，过已知点A 作线段AB=20 mm，使其平行于W 面，且与H面的倾角α=45°。

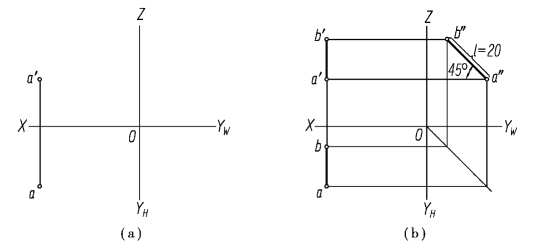
图2.13　过点A 作侧平线

分析：过点A 作平行于W 面的直线AB 为侧平线。根据侧平线的投影特性，直线AB 的侧面投影a″b″反映实长，且a″b″与OYW 轴的夹角等于其与H 面的倾角α。

作图：作图过程如图2.13（b）所示。

①作直线AB 的侧面投影。作点A 的侧面投影a″，再过a″作一条与OYW 轴成45°的直线，并在直线上截取a″b″=20 mm，a″b″即为直线AB 的侧面投影。

②作直线AB 其余两面投影。分别过a、a′作ab//OYH 轴、a′b′//OZ 轴，利用直线的侧面投影，结合投影规律即可求得直线AB 的水平投影ab 和正面投影a′b′（此题解不唯一，其他情况请读者自行分析）。