当空间两点有一个投影重合时，称这两个点是对某投影面的重合点，简称重影点，其重合的投影称为重影。此时，两点的某两个坐标相同，处于同一条投射线上。对V 面的一对重影点是正前、正后方的关系，对H 面的一对重影点是正上、正下方的关系，对W 面的一对重影点是正左、正右方的关系。

有重影，就需要判断可见性，即判断两个点中哪个可见，哪个不可见。可见性依据x、y、z坐标来判断，坐标大者可见，小者不可见，即前遮后、上遮下、左遮右。对不可见点的投影加括弧表示。

从图2.10 可知：点B 在点A 正后方，这两点的正面投影重合，点A 和点B 称为对正面投影的重影点。由于两点的x、z 坐标相同，而yA ＞yB，因此，点B 的正面投影不可见，加括弧表示。

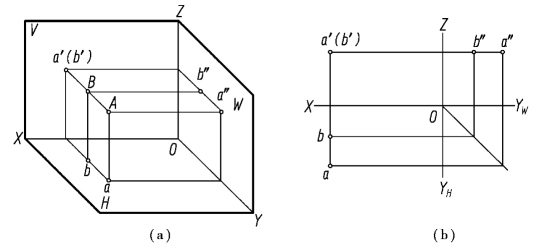
图2.10　重影点

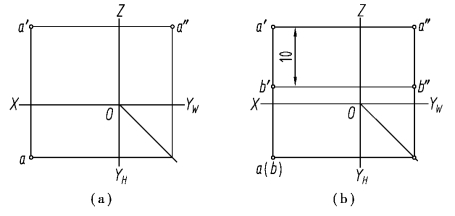
【例2.3】　如图2.11（a）所示，已知点A 的三面投影a、a′、a″，点B 在点A 的正下方10 mm处，试作出点B 的三面投影。

(www.daowen.com)

图2.11　求作点的三面投影

分析：由于点B 在点A 的正下方10 mm 处，即xA=xB、yA=yB，而zA -zB=10，所以，A、B 两点水平投影a、b 重合；又由于zA ＞zB，故b 为不可见。

作图：作图过程如图2.11（b）所示。

①由于a、b 重合，而b 不可见，故标记（b）。

②在a′正下方下量取10 mm，得b′。

③由点B 的水平投影b 和正面投影b′，求得b″。