（1）两投影面体系的建立

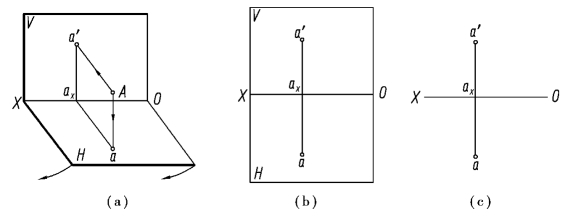
如图2.4（a）所示，设立两个互相垂直的投影面，处于正面直立位置的投影面称为正立投影面，用大写字母“V”表示，简称为正面或V 面；处于水平位置的投影面称为水平投影面，用大写字母“H”表示，简称为水平面或H 面。V 面和H 面的交线称为投影轴，用“OX”表示。

（2）点的两面投影

如图2.4（a）所示，设空间有一点A，过点A 分别向V 面和H 面作垂线，得垂足a′和a，a′称为空间点A 的正面投影，a 称为空间点A 的水平投影。同时，规定用大写字母（如A）表示空间点，其水平投影用相应的小写字母（如a）表示，正面投影用相应的小写字母加一撇（如a′）表示。

(www.daowen.com)

图2.4　点在V、H 两投影面体系中的投影

在实际作图时，为使点的两面投影画在同一平面（图纸）上，需将投影面展开。移去空间点A，规定V 面不动，将H 面绕OX 轴向下旋转90°与V 面重合，即得点A 的两面投影，如图2.4（b）所示。为作图简便，投影图中不画出投影面的边框，如图2.4（c）所示。

如图2.4（a）所示，投射线Aa 和Aa′决定的平面必然与H 面和V 面垂直，并与OX 轴交于一点ax，Aaaxa′是一个矩形，OX 轴垂直于该矩形平面。因此，在展开后的投影图上，a、ax、a′三点必在同一条直线上，且a′a⊥OX 轴，aax=Aa′，a′ax=Aa。由此可得出点在两投影面体系中的投影规律：

①点的正面投影和水平投影的投影连线垂直于OX 轴，即a′a⊥OX。

②点的正面投影到OX 轴的距离反映空间点到H 面的距离，点的水平投影到OX 轴的距离反映空间点到V 面的距离，即a′ax=Aa，aax=Aa′。