以上讨论的是液体介质，波源作活塞振动，辐射连续波等理想条件下的声场，简称为理想声场。实际检测中往往是固体介质，波源非均匀激发，辐射脉冲波声场简称为实际声场。它与理想声场是不完全相同的。

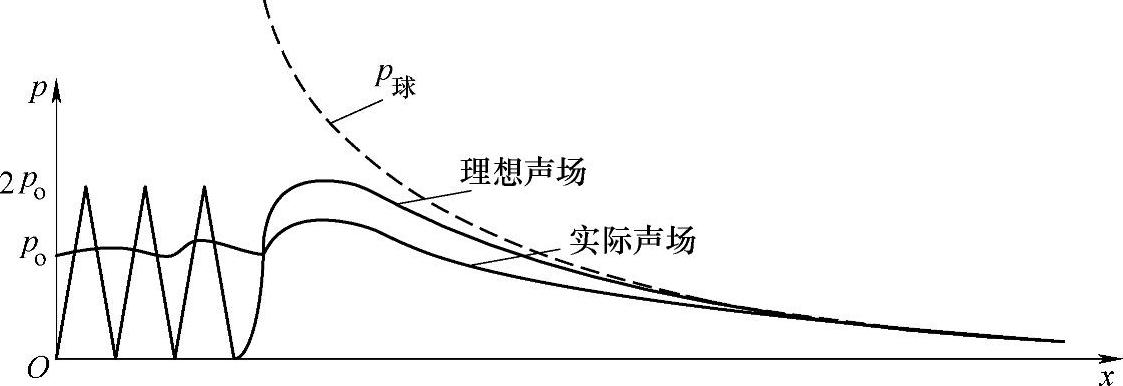
图2-12 实际声场与理想声场声压比较

由图2-12可知，实际声场与理想声场在远场区轴线上的声压分布基本一致。这是因为，当与波源间的距离足够远时，波源各点至轴线上某点的波程差明显减小，从而使波的干涉大大减弱，甚至不产生干涉。但在近场区内，实际声场与理想声场存在明显区别。理想声场轴线上声压存在一系列极大值和极小值，且极大值为2p_o，极小值为零。实际声场轴线上声压虽然也存在极大值与极小值，但是波动幅度小，极大值远小于2p_o，极小值也远大于零，同时极值点的数量明显减少。这可以从以下几方面来分析其原因。

1）近场区出现声压极值点是由波的干涉造成的。理想声场是连续波，波源各点辐射的声波在声场中某点产生完全干涉。实际声场是脉冲波，脉冲波持续时间很短，波源各点辐射的声波在声场中某点产生不完全干涉或不产生干涉，从而使实际声场中的近场区轴线上的声压变化幅度小于理想声场，极值点减少。

2）根据傅里叶级数，脉冲波可以视为常数项和无限个n倍基频的正弦波、余弦波之和。设脉冲波函数为f（t），则

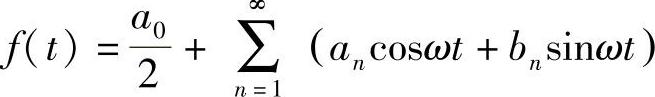
式中 t——时间；

n——正整数；

ω——圆频率，ω=2πf=2πT；

a₀、a_n、b_n——由f（t）决定的常数。

由于脉冲波是由许多不同频率的正弦波、余弦波组成的，每种频率的波决定一个声场，因此总声场就是各不同声场的叠加。(www.daowen.com)

由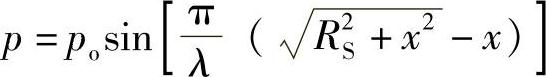可知，波源轴线上的声压极值点位置随着波长λ的变化而变化，不同f的声场极值点不同，它们互相叠加后总声压就趋于均匀，使近场区声压分布不均的情况得到改善。

脉冲波声场某点的声压可用下述方法来求得。设声场中某处的总声强为I，则

I=I₁+I₂+I₃+…+In

即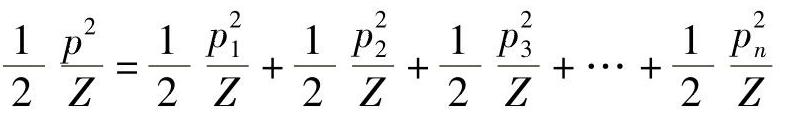

所以超声场中该处的总声压p为

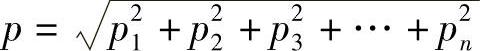
式中 I_n——频率为f_n的谐波引起的声强；

p_n——频率为f_n的谐波引起的声压。

3）实际声场的波源是非均匀激发的，波源中心振幅大，边缘振幅小，由波源边缘引起的波程差较大，对干涉影响也较大。因此，这种非均匀激发的实际波源产生的干涉要小于均匀激发的理想波源。当波源的激发强度按高斯曲线变化时，近场区轴线上的声压将不会出现极大值或极小值，这就是高斯探头的优越性。

4）理想声场是针对液体介质而言的，而实际检测对象往往是固体介质。在液体介质中，液体内某点的压强在各个方向上的大小是相同的。波源各点在液体中某点引起的声压可视为同方向上进行线性叠加。在固体介质中，波源某点在固体中某点引起的声压方向在二者连线上。对于波源轴线上的点，由于对称性，使垂直于轴线方向的声压分量互相抵消，使轴线方向的声压分量互相叠加。显然，这种叠加干涉要小于液体介质中的叠加干涉，这也是实际声场近场区轴线上声压分布较均匀的一个原因。