1.波源轴线上声压的分布
在连续简谐纵波且不考虑介质衰减的条件下,图2-1所示的液体介质中圆盘波源上的一个点波源dS辐射的球面波在波源轴线上Q点引起的声压为
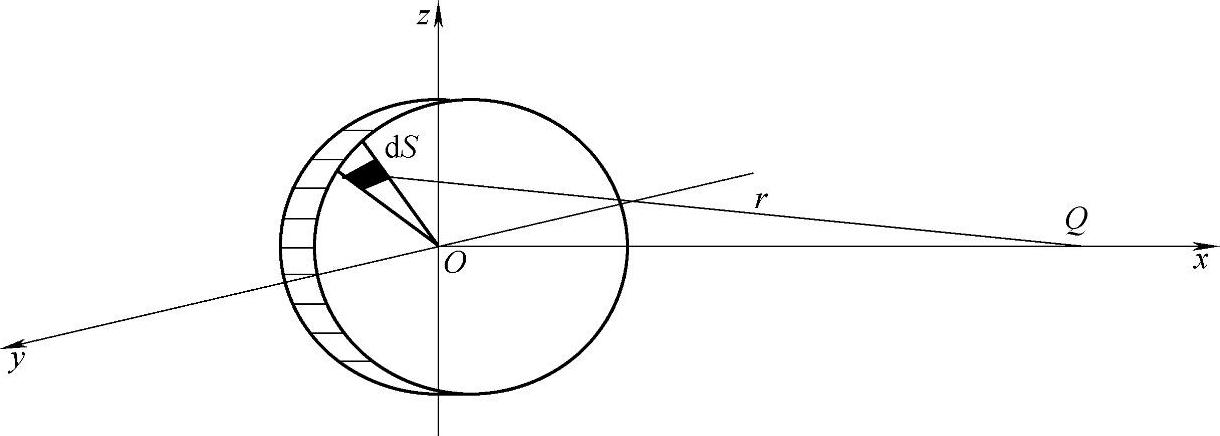
图2-1 圆盘波源轴线上声压推导图
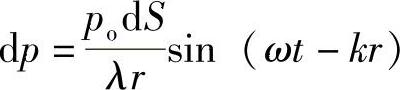
式中 po——波源的起始声压;
dS——点波源的面积;
λ——波长;
r——点波源到Q点的距离;
k——波数,k=ω/c=2π/λ;
ω——圆频率,ω=2πf;
t——时间。
所以对整个波源面积进行积分就可以得到波源轴线上任意一点的声压,即
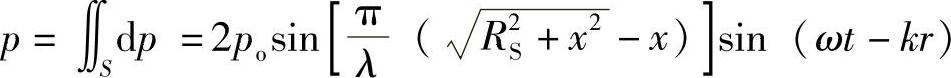
其声压幅值为
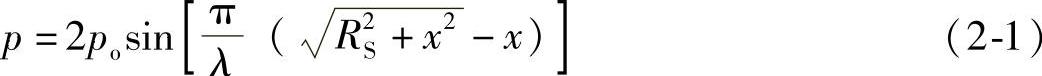
式中 RS——波源半径;
x——轴线上Q点至波源的距离。
当x≥2RS时,根据牛顿二项式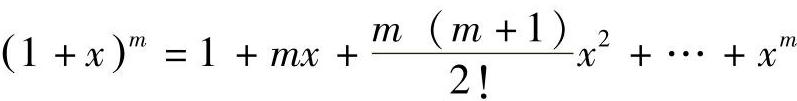 ,由于RS/x≤1/2,将式(2-1)简化为
,由于RS/x≤1/2,将式(2-1)简化为
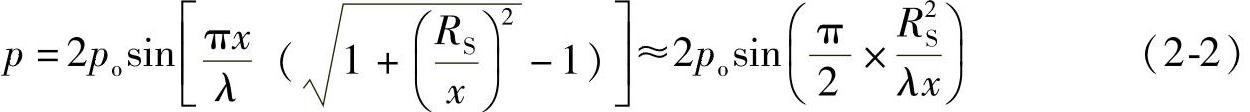
当x≥3R2S/λ时(即πR2S/2λx≤π/6时),根据sinθ≈θ(θ很小时),上式可简化为

式中 FS——波源面积,FS=πR2S=πD2S/4(DS为波源直径)。
式(2-3)表明,当x≥3R2S/λ时,圆盘波源轴线上的声压与距离成反比,与波源面积成正比。波源轴线上的声压随着距离变化的情况如图2-2中的实线所示。
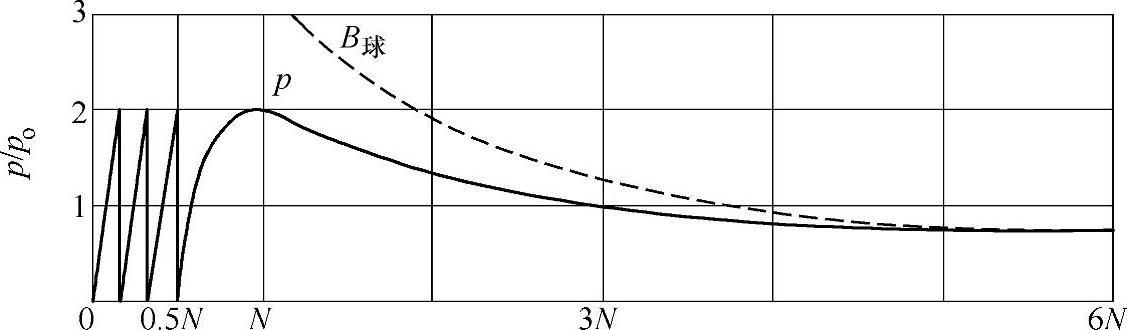
图2-2 圆盘波源轴线上声压的分布
(1)近场区 波源附近由于波的干涉而出现一系列声压极大值和极小值的区域,称为超声场的近场区,又称为菲涅耳区。近场区中的声压分布不均的原因是波源各点至轴线上某点的距离不同,存在波程差,互相叠加时存在相位差而互相干涉,使某些地方声压相互加强,另一些地方互相减弱,于是就出现了声压极大值与极小值的点。
波源轴线上最后一个声压极大值至波源的距离称为近场区长度,用N表示。当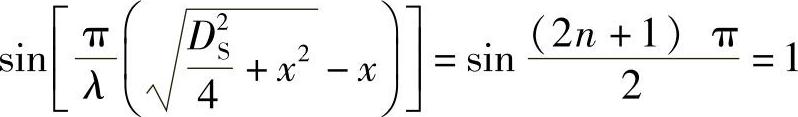 时,声压p有极大值,化简得极大值对应的距离为
时,声压p有极大值,化简得极大值对应的距离为
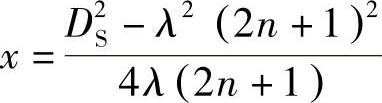
式中 n——0,1,2,3,…,小于(DS-λ)/2λ的正整数,共有n+1个极大值,其中n=0为最后一个极大值。
因此近场区长度为
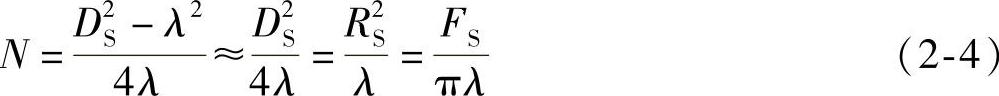
当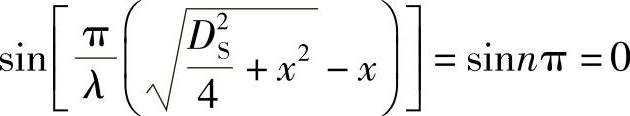 时,p有极小值,化简得极小值对应的距离为
时,p有极小值,化简得极小值对应的距离为
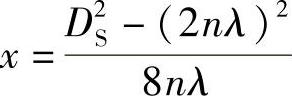
式中 n——0,1,2,3,…,小于DS/2λ的正整数,共n有个极小值。
由式(2-4)可知,近场区长度与波源面积成正比,与波长成反比。
在近场区检测定量是不利的,因为处于声压极小值处的较大缺陷回波可能较低,而处于声压极大值处的较小缺陷回波可能较高,这样就容易引起误判甚至漏检,所以应尽可能避免近场区检测定量。
(2)远场区 波源轴线上至波源的距离x>N的区域称为远场区。远场区轴线上的声压随着距离的增加单调减小。当x>3N时,声压与距离成反比,近似球面波的规律,p=poFS/λx,如图2-2中虚线所示。这是因为当距离x足够大时,波源各点至轴线上某一点的波程差很小,引起的相位差也很小,这时干涉现象可忽略不计,所以远场区轴线上不会出现声压极大值或极小值。
2.超声场横截面上声压的分布
超声场近场区与远场区各横截面上的声压分布是不同的,如图2-3和图2-4所示。
 (https://www.daowen.com)
(https://www.daowen.com)
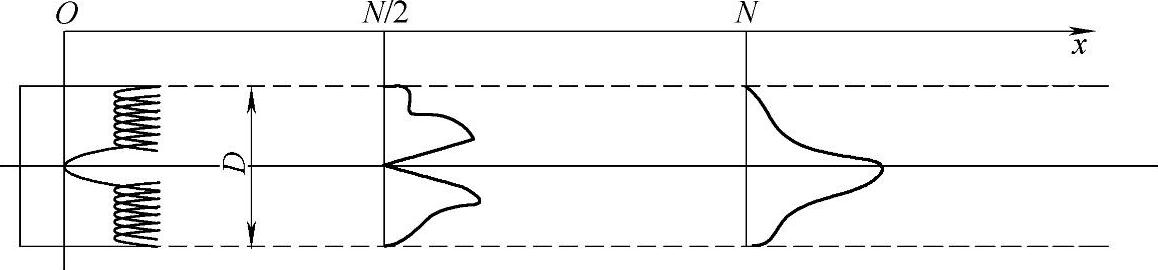
图2-3 圆盘波源(D/λ=16)近场区中x=0,x=N/2,x=N的横截面上的声压分布
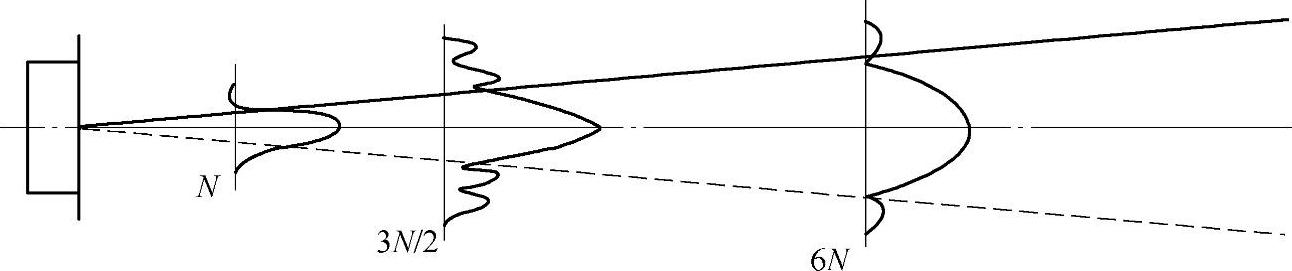
图2-4 圆盘波源(D/λ=16)远场区中x=N,x=3N/2,x=6N的横截面上的声压分布
在x<N的近场区内,存在中心轴线上声压为0的截面,如x=0.5N处的截面,中心声压为0,偏离中心声压较高。在x>N的远场区内,轴线上的声压最高,偏离中心声压逐渐降低,且同一横截面声压的分布是完全对称的。在实际检测中,测定探头波束轴线的偏离和横波斜探头的K值时,规定要在2N以外进行就是缘于此。
3.波束指向性和半扩散角
远场区中任意一点声压推导图如图2-5所示。
点波源dS在至波源充分远处任意一点M处引起的声压为
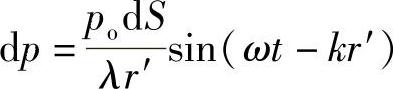
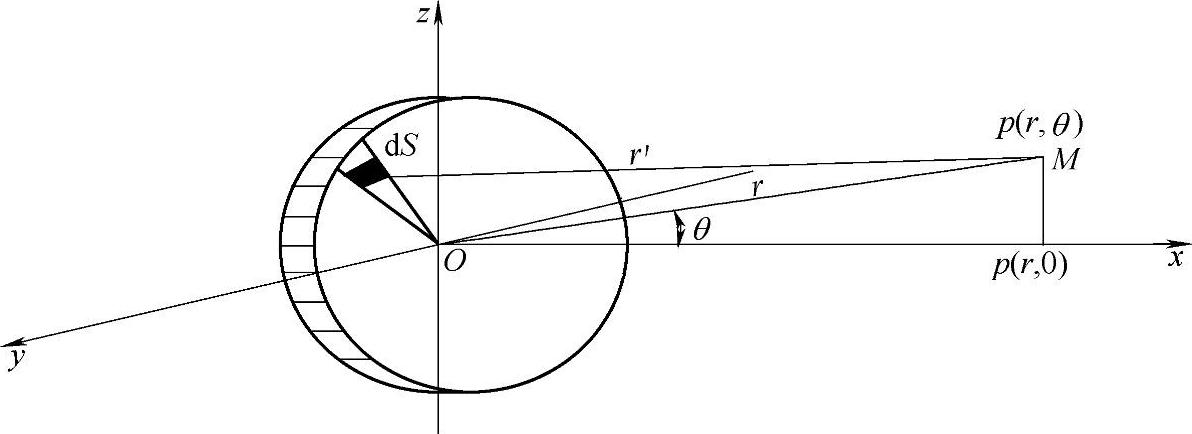
图2-5 远场区中任意一点声压推导图
整个圆盘波源在点M处引起的总声压幅值为

式中 r——点M至波源中心的距离;
θ——r与波源轴线的夹角;
J1——第一类贝塞尔函数。
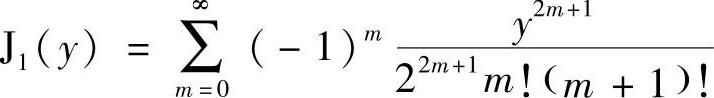
波源前充分远处任意一点的声压p(r,θ)与波源轴线同距离处声压p(r,0)之比,称为指向性系数,用Dc表示。
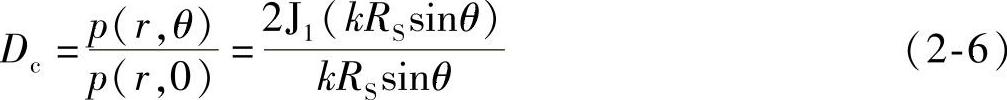
令y=kRSsinθ,则
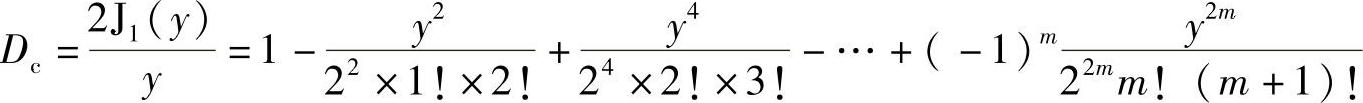
Dc与y的关系如图2-6所示。由图2-6可知:
1)Dc=p(r,θ)/p(r,0)≤1。这说明超声场中至波源充分远处同一横截面上各点的声压是不同的,以轴线上的声压为高。只有当波束轴线垂直于缺陷界面时,缺陷回波才最高。
2)当y=kRSsinθ=3.83,7.02,10.17等时,Dc=p(r,θ)/p(r,0)=0,即p(r,θ)=0。这说明圆盘波源辐射的声束截面声场中存在一些声压为零的点。由y=kRSsinθ=3.83得
θ0=arcsin1.22λ/DS≈70λ/DS (2-7)
式中 θ0——圆盘波源辐射的纵波声场的第一零值发散角,又称为半扩散角。
3)当y>3.83,即θ>θ0时,|Dc|<0.15。这说明半扩散角θ0以外的声场声压很低,超声波的能量主要集中在半扩散角θ0以内。因此,可以认为半扩散角限制了波束的范围。只有当缺陷位于主波束范围时,2θ0以内的波束为主波束才容易被发现。以确定的扩散角向固定的方向辐射超声波的特性称为波束指向性。
4)在超声波主波束之外存有一些副膜,由于副膜能量很低和介质对超声波的衰减作用,其从波源附近传播后衰减很快。
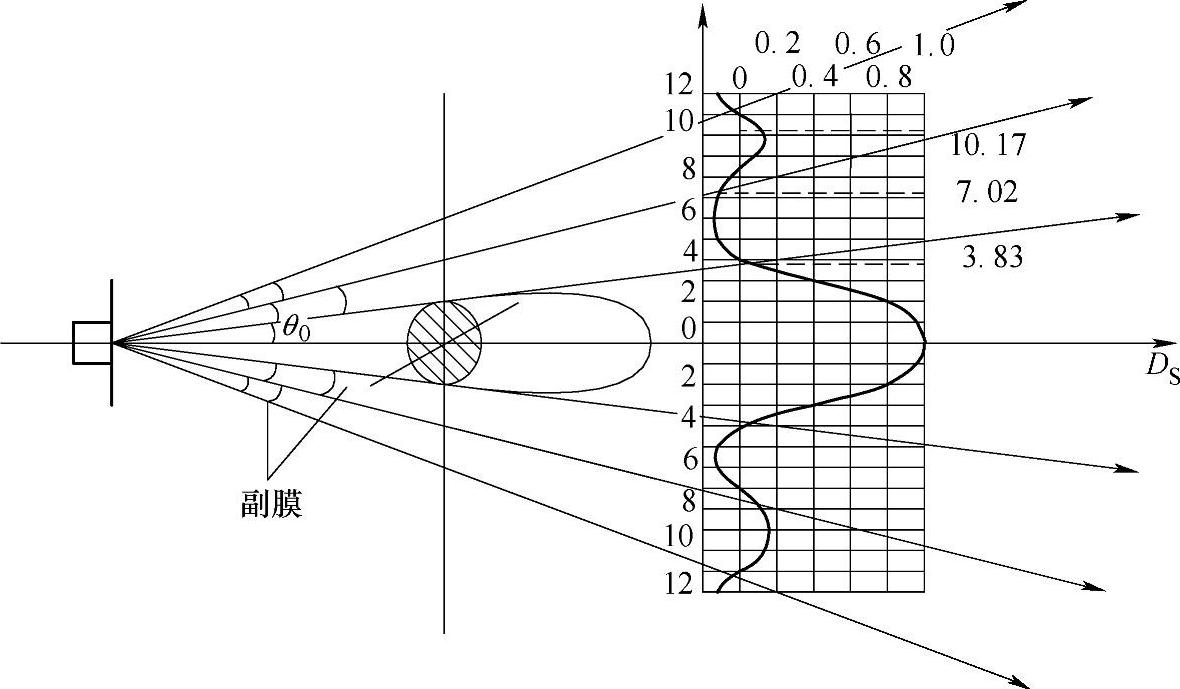
图2-6 圆盘波源波束指向性
5)由θ0=70λ/DS可知,增加探头直径DS,提高检测频率f,半扩散角θ0将减小,即可以改善波束指向性,使超声波的能量更集中,有利于提高检测灵敏度。但由N=D2S/4λ可知,增大DS和f,近场区N长度增加,对检测不利。因此,在实际检测中要综合考虑DS和f对θ0和N的影响,应合理选择DS和f,一般是在保证检测灵敏度的前提下尽可能减少近场区长度。
4.波束未扩散区与扩散区
超声波波源辐射的超声波是以特定的角度向外扩散出去的,但并不是从波源开始扩散的,而是在波源附近存在一个未扩散区b,其理想化的形状如图2-7所示。
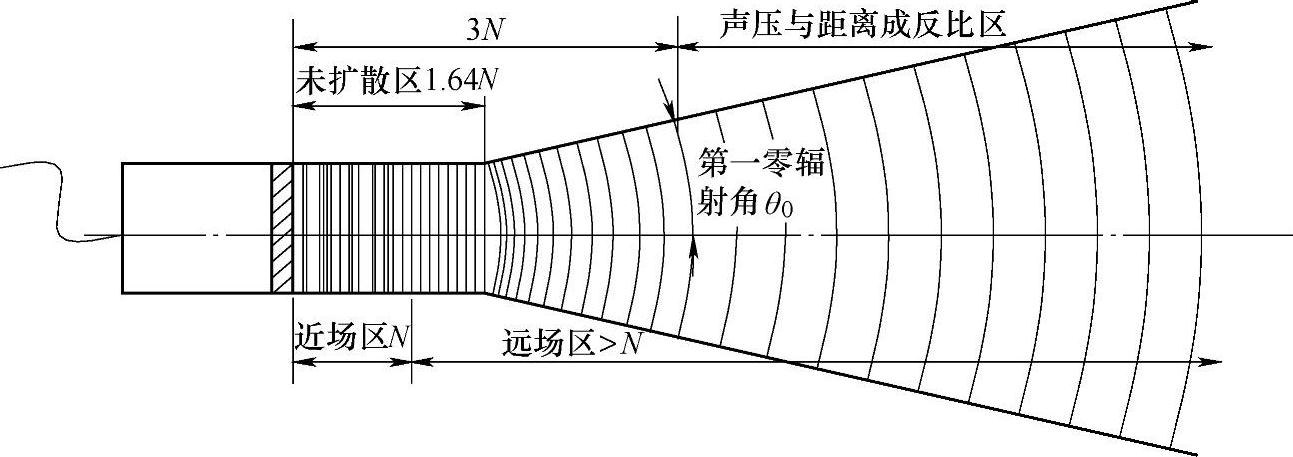
图2-7 圆盘波源理想化声场中的波束未扩散区和扩散区
由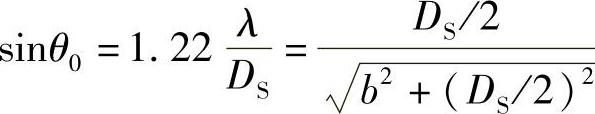 得
得

在波束未扩散区b内,波束不扩散,不存在扩散衰减,各截面平均声压基本相同,因此薄板试块前几次底波相差无几。
到波源的距离x>b的区域称为扩散区。扩散区内波束扩散,存在扩散衰减。
例2-1用f=2.5MHz,DS=20mm的探头检测波速cL=5900m/s的工件,那么近场区长度N、半扩散角θ0和未扩散区b分别为
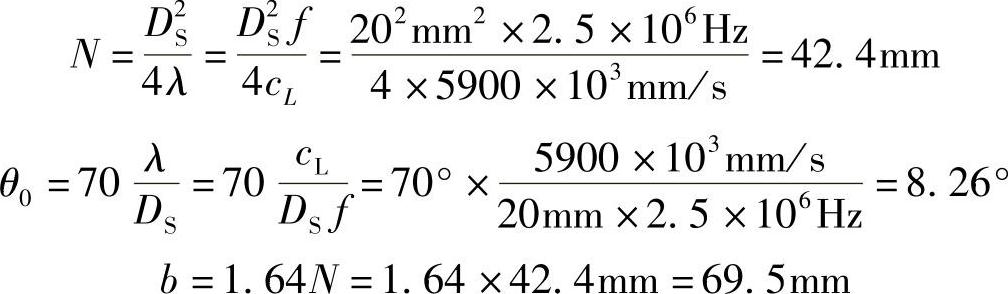
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







