超声波的波速与波型、介质（性质和形状）和温度有关。

1.固体弹性介质中的超声波

其波速计算公式为

式中 E——弹性模量；

ρ——介质密度；

K——与材料泊松比有关的常数，由波型决定，对于确定的波型，其有确

定值。

纵波波速计算公式为

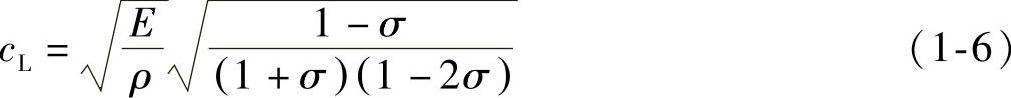
横波波速计算公式为

表面波波速计算公式为

式中 σ——泊松比（0<σ<1）；

G——切变模量；

E——弹性模量；

ρ——介质密度。

对比上面的公式，纵波波速（c_L）>横波波速（c_S）>表面波波速（c_R）。对于一般材料，c_L≈2c_S，c_R≈0.9c_S。

由此可知：在同一介质中传播时，纵波波速最快，横波波速次之，表面波波速最慢；若波动频率相同，则在同一介质中纵波波长最长，横波波长次之，表面波波长最短。由于缺陷检出能力和分辨能力均与波长有关，波长越短，检测灵敏度一般越高。因此，纵波对缺陷的检出能力和分辨率要低于横波。(www.daowen.com)

2.液体介质超声波

液体介质中超声波波速的计算公式为

式中 K_a——液体的体积模量（或称为体积膨胀系数），是温度的函数；

ρ——介质密度。

3.钢质细棒中的超声波

钢质细棒中超声波的波速c_D≈0.9 c_L。

超声波的波速一般随着介质温度的升高而降低，所以在高温状态下，超声波检测必须考虑由波速的变化而引起的缺陷定位和定量的误差。

但超声波在水中的波速却是一个例外，水浸法检测中的介质是水。

水中波速的计算公式为

c_L=1557-0.0245×（74-T_K）² （1-10）

式中 T_K——水的温度（℃）。

由式（1-10）可以看出：当水温低于74℃时，超声波的波速随着温度的升高而增大；当水温高于74℃时，超声波的波速随着温度的升高而降低；当水温等于74℃时，超声波的波速最大。

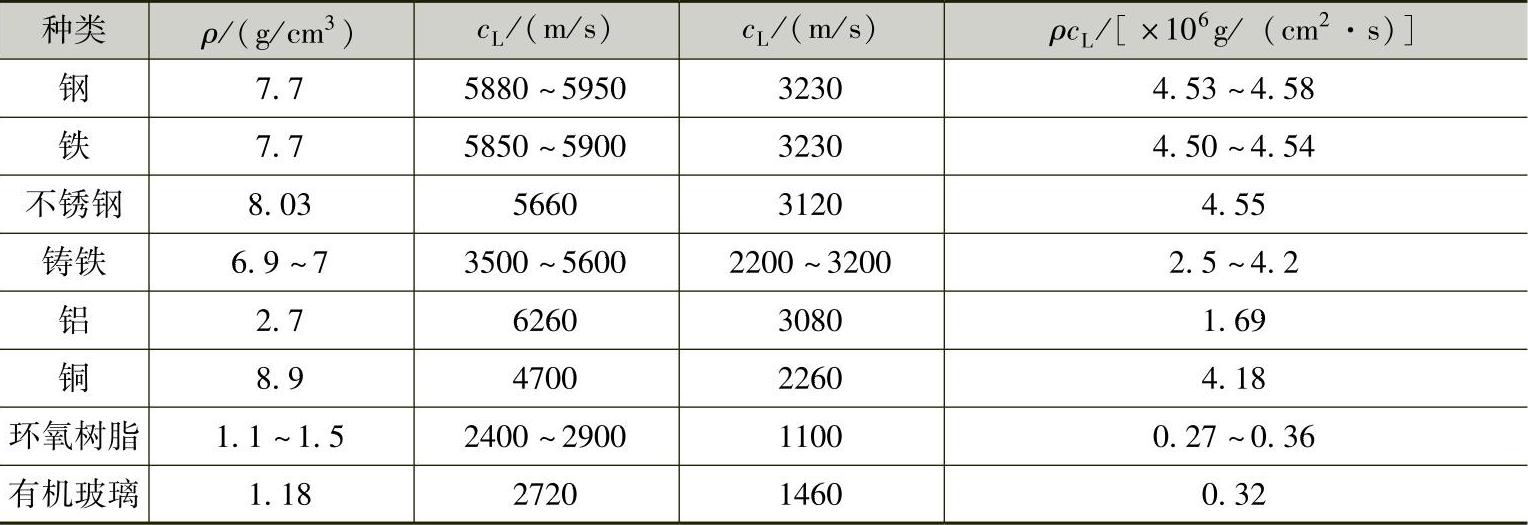
介质密度、声速及声特性阻抗见表1-1和表1-2。

表1-1 液体或气体的密度、波速及声特性阻抗

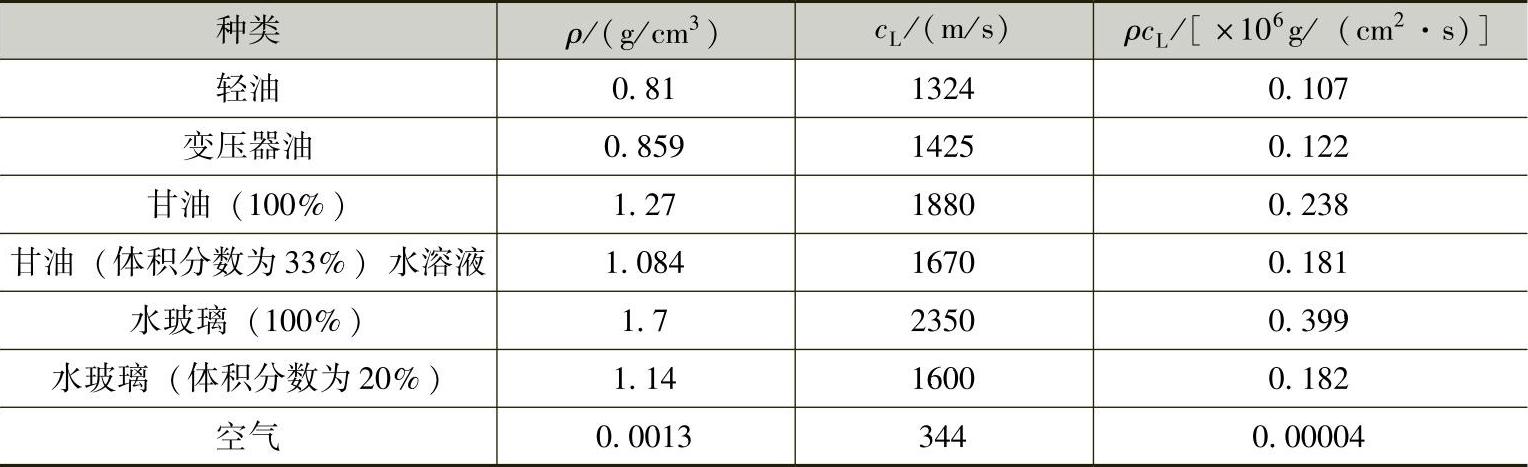
表1-2 固体的密度、波速及声特性阻抗