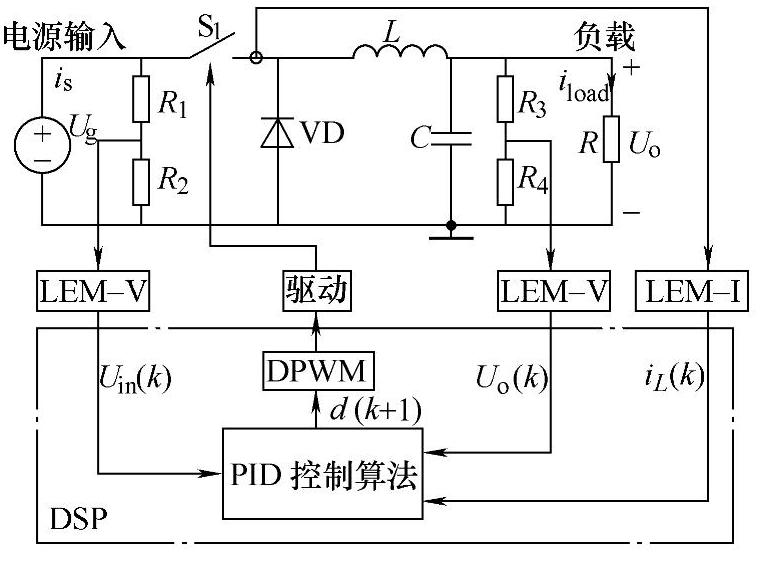
图4-98 基于DSP数字控制的Buck变换器系统图

1.变换器的结构与仿真

图4-98所示为基于DSP数字控制的Buck变换器系统示意图。主电路为Buck变换器，控制电路采用DSP，控制策略采用传统的PID。其中Buck变换器的参数为：已知U_g=15V，U=5V，R_L=10Ω，L=40μH，C=560μF，f_s=30kHz。用交流小信号建模方法，根据已知参数可得Buck变换器控制-输出传递函数为：

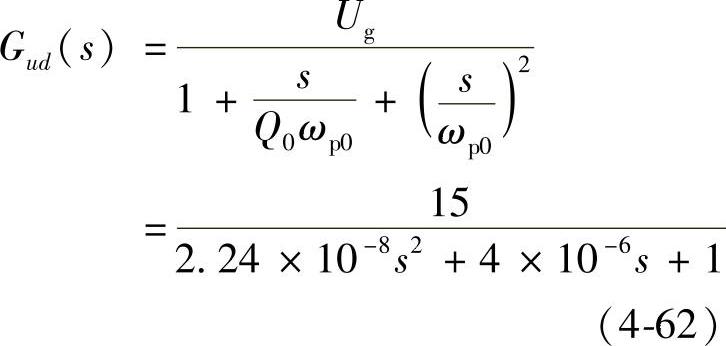
式中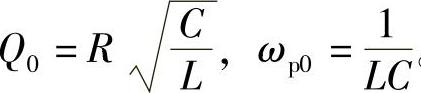，。系统的开环增益K=15，阻尼比ξ=0.0134，品质因数Q=37.42，自然谐振角频率ω_p0=6.68×10³rad/s。

2.系统开环时域特性仿真

根据式（4-62），可通过仿真了解系统的开环特性。首先编写Matlab命令语句如下：

num=15；

den=[2.24e-84e-61]；

step（num，den）

将上述命令输入到Matlab环境，运行可得如图4-99所示的阶跃响应曲线。由图可见：上升时间短，系统的阻尼比过小，其计算值为ξ=0.0134，系统的品质因数过大，其计算值为Q=37.42，超调量过大，本例中接近200%。超调量过大，将会导致系统能量损耗较大，同时调节时间增长。为了改善系统的动态性能和稳态性能，应该为其设计合适的控制器。

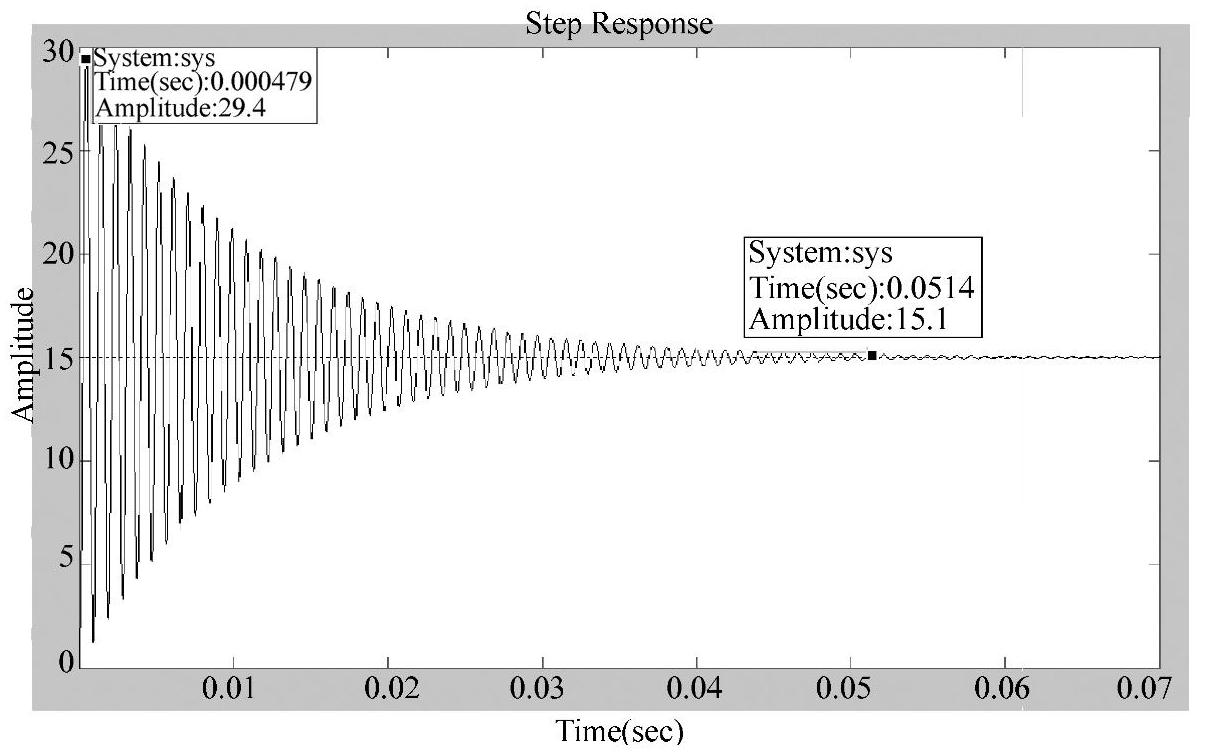
图4-99 系统开环阶跃响应曲线

3.系统开环频域特性仿真

方法1：用前面介绍的对开关网络建模的方法，在OrCAD/Capture界面中建立CCM1平均开关网络的PSpice子电路模型，将所建的子电路CCM1嵌入到PSpice用户库中，即可像其他元器件一样调用。Buck变换器控制-输出传递函数的仿真电路如图4-100所示。图中，在表示占空比的直流电压源V2上叠加了一个幅值为10mV的低频交流扰动电压源V2，其仿真控制-输出传递函数所用的表达式为

Buck变换器控制-输出传递函数的频率特性如图4-101所示，从图中可见，穿越频率f_c=4.2489kHz，相角裕量φ_m≈0°，可见系统处于临界稳定状态，无法正常工作，需设计相应的控制器。

方法2：将式（4-62）输入到Matlab仿真软件中也可对系统开环频率特性进行仿真。

将式（4-62）用Matlab语句编程仿真，需编制Matlab语句如下：

numC=[15]；

denC=[2.24e-84e-61]；

sysC=tf（numC，denC）；

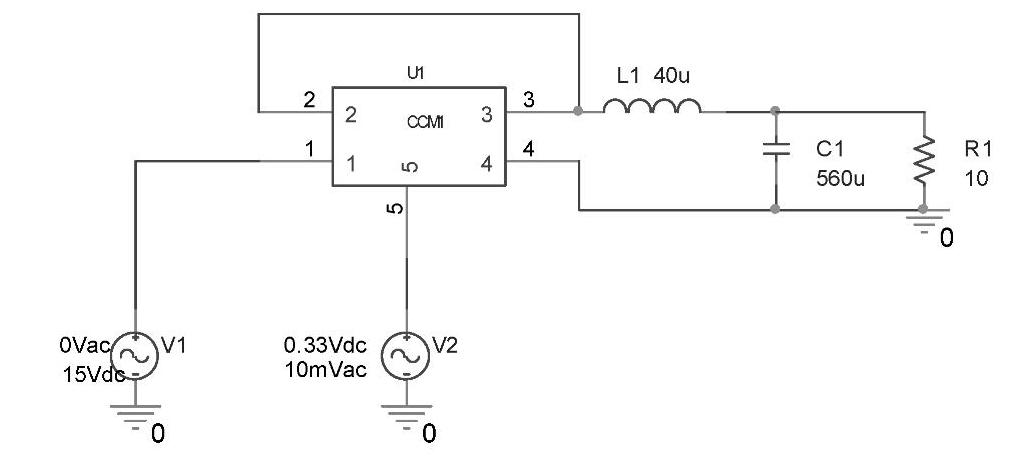
图4-100 Buck变换器控制一输出传递函数的仿真电路

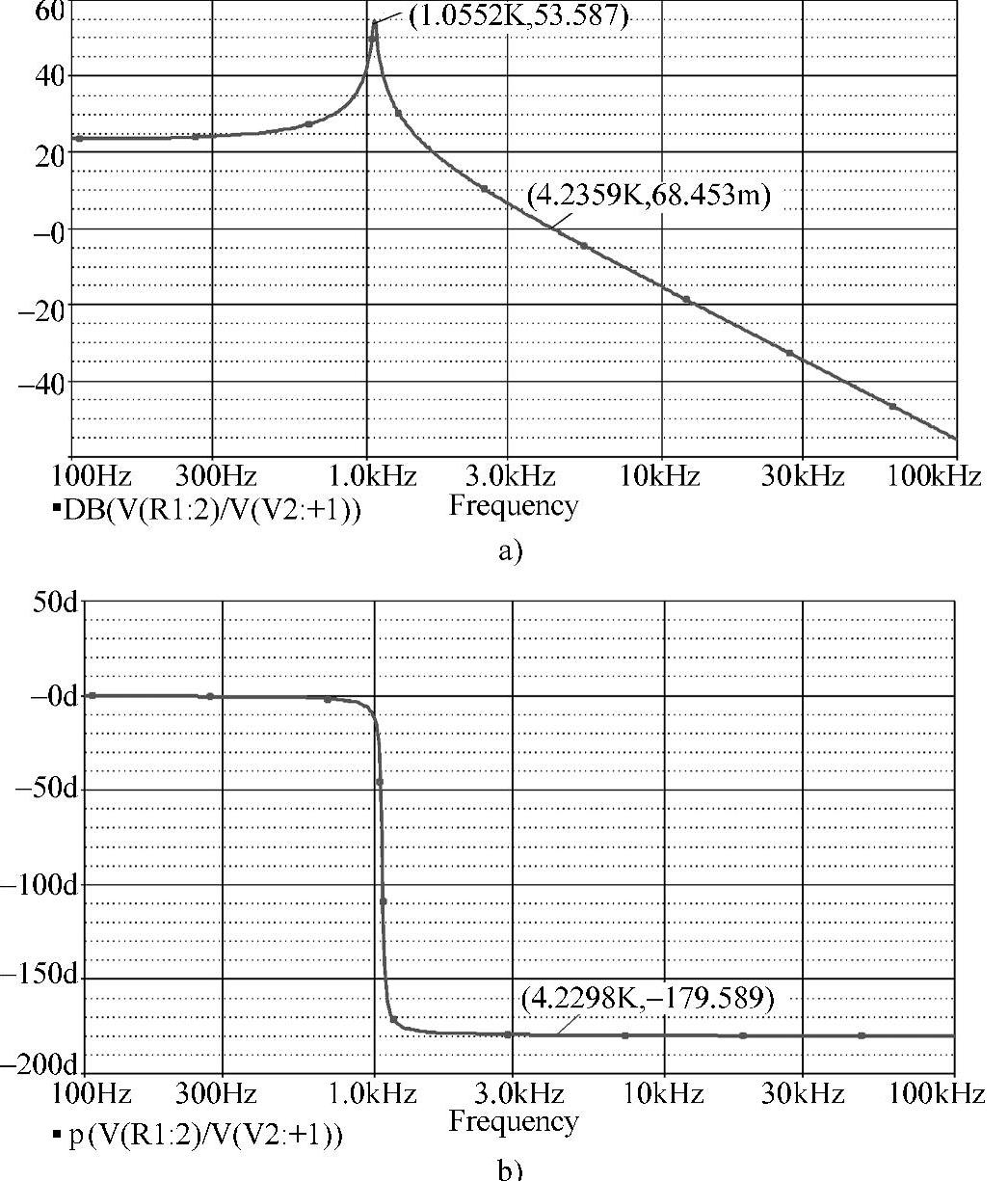
图4-101 用PSpice仿真的Buck变换器控制-输出传递函数的频率特性曲线

a）幅频特性 b）相频特性

figure（1），bode（sysC），grid on；

将上述命令输入到Matlab环境进行处理，运行后得到图4-102所示曲线。比较图4-101和图4-102可得出两种方法都可用于仿真系统的开环频率特性。

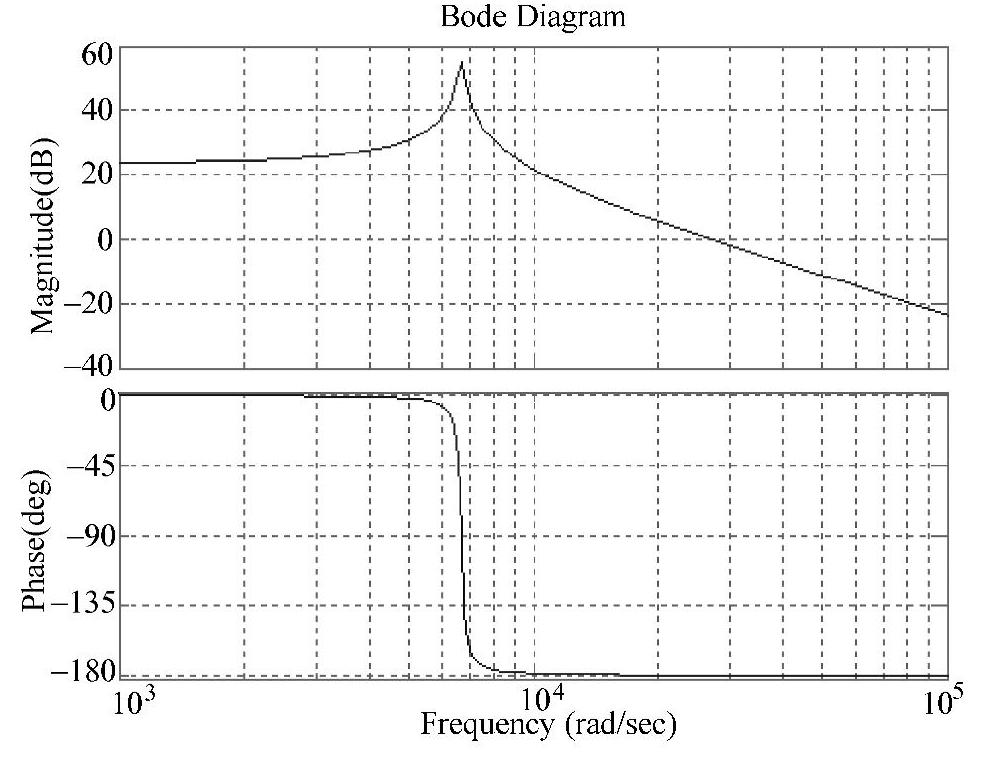
图4-102 用Matlab仿真的Buck变换器控制-输出传递函数

值得一提的是，也可将式（4-62）输入到Mathcad仿真软件中，同样可得到系统开环频率特性，此处不赘述。设计者可根据对各仿真软件的熟悉程度，选择不同的仿真方法来获得系统开环频率特性。

开关调节系统的稳态性能主要取决于开环传递函数博德图的低频段，要求其直流增益无限大、以-20dB/dec的斜率下降；动态性能主要取决于开环传递函数博德图的中频段，要求幅频特性以-20dB/dec斜率下降并穿越0dB线的频段，有适当大的中频带宽h和合适的穿越角频率ω_c；在高频段，理想幅频特性应以-40dB/dec斜率下降。理想开环传递函数的频率特性如图2-11所示。为了得到系统的理想特性，需要为该系统添加控制器以调整系统频率特性。

图4-101a所示的仿真特性显然不符合理想开环传递函数的频率特性，因此，要设计控制器对系统进行补偿。

4.数字控制器设计与系统仿真

本文以数字PID为讨论对象。设根据GB/T 14714—2005《微小型计算机系统设备用开关电源通用规范》对输出电压为5V的电源指标为设计指标，该标准指出，暂态恢复时间最大值应小于50ms，最小调节范围±5%。本例中U+ΔU=5±0.01V，则本例的设计指标为

超调量：σ≤0.2%；调节时间：t_s＜50ms。

（1）PID控制

加入PID控制器后开关调节系统的结构示意图如图4-103所示。图中，G_ud（s）是Buck变换器从控制-输出的传递函数，PID是需要设计的控制器。

设PID控制器的传递函数为G_c（s），则有

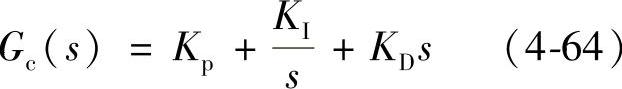
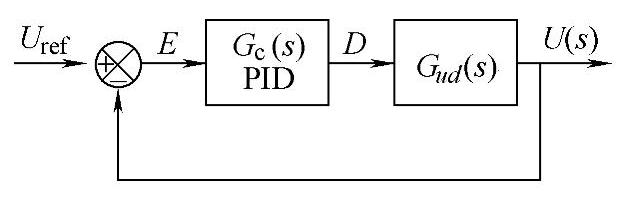
图4-103 控制系统结构图

PID控制的实质是：控制器分别对误差信号进行比例、积分与微分运算，用运算结果的加权和构成系统的控制信号D（s），从而对被控对象进行控制。P（Proportional）：比例控制是最简单的控制结构，但它也能使系统满足某一方面的特性要求，如GM、PM、稳态误差等；D（Differential）：加入微分控制，增加阻尼作用；I（Integral）：加入积分控制，则增加了系统的稳态误差精度^[48]。

（2）用仿真分析方法确定K_P、K_I和K_D

PID控制器的设计的关键在于确定K_P、K_I和K_D这三个参数。而这三个参数一般是根据经验来确定，但对于初学者在没有实践经验的情况下，可参照文献[48]的方法确定这三个参数。这里利用Matlab仿真工具，用仿真分析的方法来选定参数，确定K_P、K_I和K_D，以提高PID控制器设计的效率。

1）确定K_P值

关于K_P的确定，首先可以根据根轨迹找出K限点，然后利用阶跃响应确定K_P大致范围，从而获得系统闭环稳定的增益范围。为了获得K_P的大致范围，需编制Matlab语句如下：

G=tf（15，[2.24e-84e-61]）；

KP=[1：4：20]；

for i=1：length（KP）

G_c=feedback（KP（i）*G，1）；

step（G_c），hold on

end

figure；rlocus（G），axis（＇spuare＇）；

k=rlocfind（G）

将上述命令输入到Matlab环境进行处理，运行后得到如图4-104和图4-105所示的曲线。由图4-104可知K_P的取值范围不得小于0.0112。将如图4-105所示的阶跃响应曲线放大，可看出第3至第4条曲线的K_P值在9～13的情况较好。本设计暂定K_P=10。从图4-105所示中还可得出本系统只采用比例调节是无法达到设计要求的，还需加入积分调节和微分调节。(www.daowen.com)

2）确定K_I值

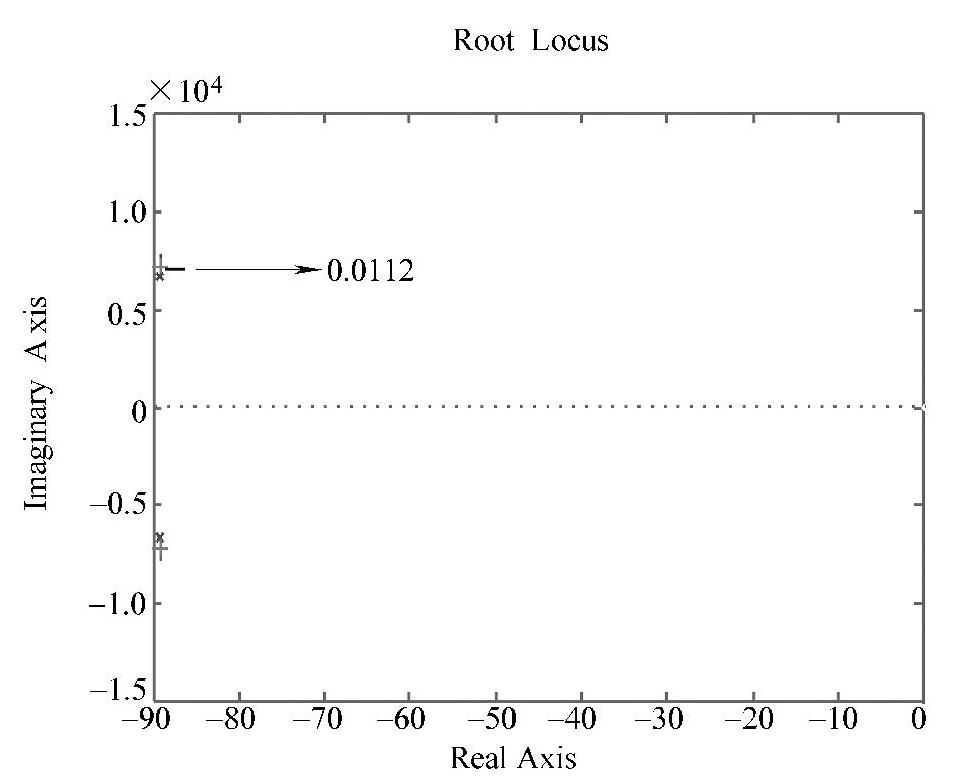
图4-104 系统的根轨迹

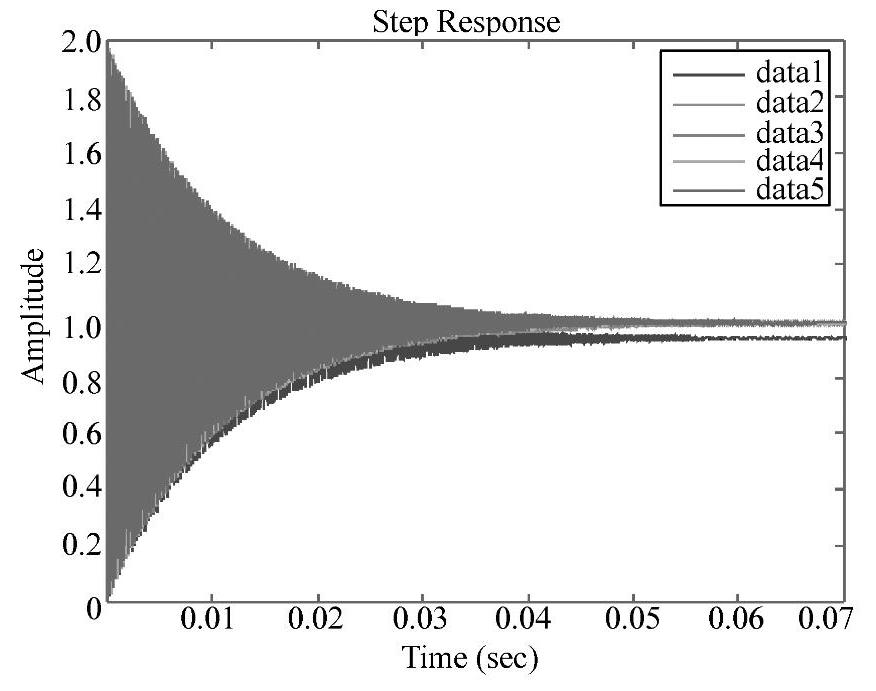
图4-105 不同K_P值下的闭环系统阶跃响应

在确定了K_P后，需确定积分系数K_I。为了获得K_I的大致范围，需编制Matlab语句如下：

G=tf（15，[2.24e-84e-61]）；

KP=10；

KI=[1e-3：2e-3：1e-2]；

for i=1：length（KI）

Gc=tf（[KP，KI（i）]，[1，0]）；

G_c=feedback（G*Gc，1）；

step（G_c），hold on

end

将上述命令输入到Matlab环境进行处理，运行结果如图4-106所示。从图中局部曲线放大可以看出第2至第3条曲线的K_I取值范围在0.003～0.005之间的情况较好，因此取K_I=0.003。

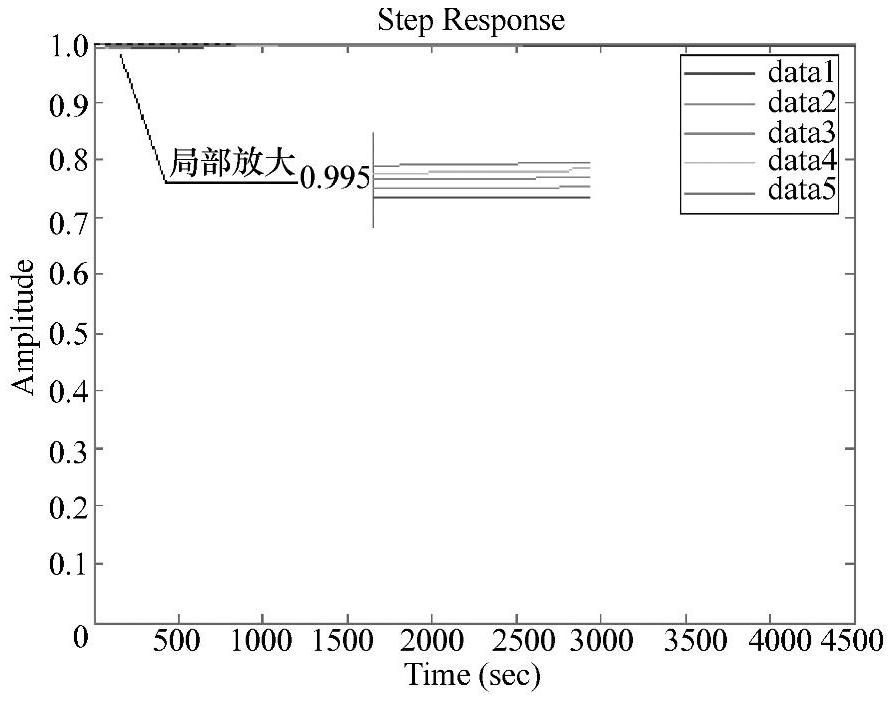
图4-106 PI控制下闭环系统阶跃响应曲线

3）确定K_D值

选定了K_P=10和K_I=0.003后，可确定K_D值，为了获得K_D的大致范围，需编制Matlab语句如下：

G=tf（15，[2.24e-84e-61]）；

KP=10.0；KI=3e-3；KD=[1e-3：2e-3：1e-2]；

for i=1：length（KD）

Gc=tf（[KD（i）KP KI]，[1，0]）；

G_c=feedback（G*Gc，1）；

step（G_c），hold on

end

将上述命令输入到Matlab环境进行处理，运行结果如图4-107所示，从图中可看出K_D的取值在0.003左右较好，因此取K_D=0.00222。

（3）采用PID校正后系统闭环仿真

在确定了PID控制器的K_P、K_I和K_D三参数后，为了获得校正后系统的闭环阶跃响应，根据图4-103所示的系统，可编制如下程序：

G=tf（[15]，[2.24e-84e-61]）；

KP=10；KI=0.003；KD=2.22e-3；

Gc=tf（[KD KP KI]，[1，0]）；

G_c=feedback（G*Gc，1，-1）；

step（5*G_c，0.0001），hold on

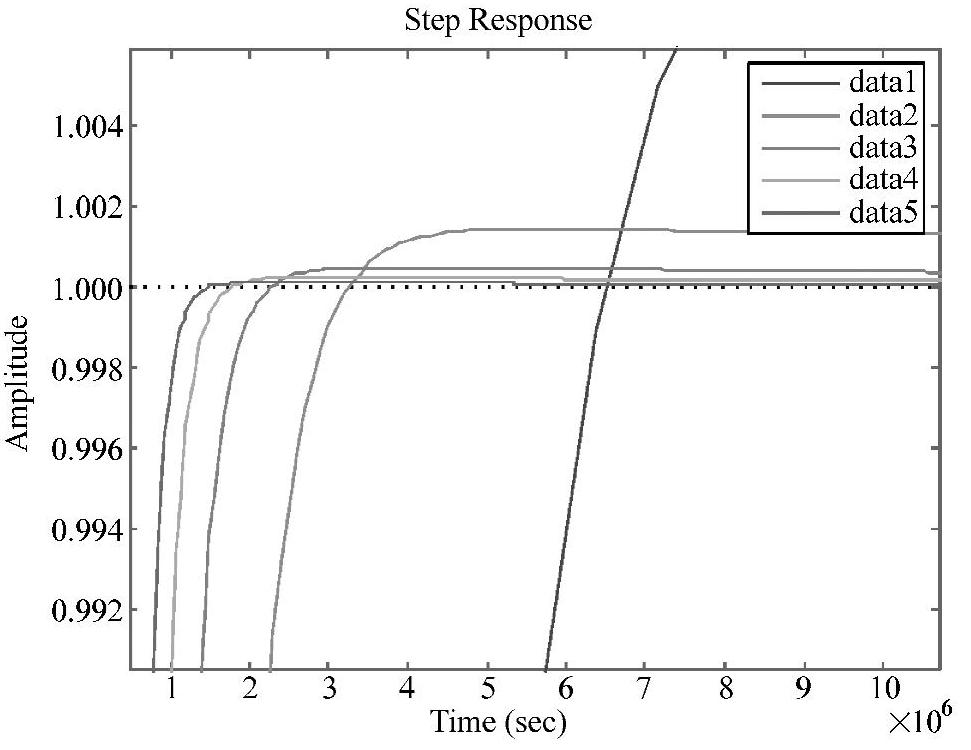
图4-107 PID控制下闭环系统阶跃响应曲线

将上述程序输入Matlab环境下运行，可得到如图4-18b所示的阶跃响应。为了得到更直观的输出电压为5V的阶跃响应，在上述阶跃语句中乘了系数5。

图4-108a所示是未加入PID控制系统的闭环阶跃响应，比较如图4-108a和b所示的系统闭环阶跃响应，加入PID后系统可得到满意的闭环响应特性。从如图4-108b所示可见，超调量为0.2%；调节时间为5.8×10^-2ms＜45ms，满足设计指标。由此可得到PID控制器传递函数为

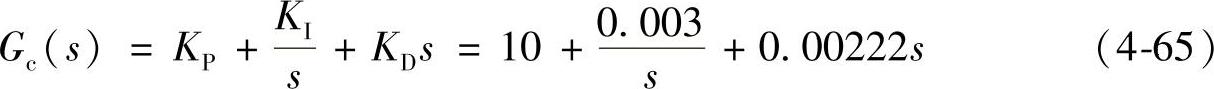
经补偿后系统开环传递函数为

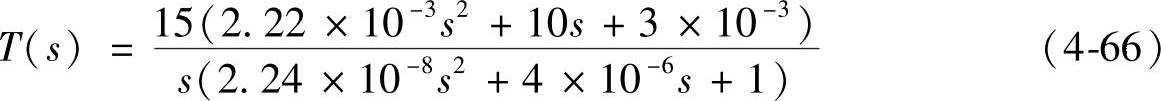
计算机控制是一种采样控制，连续PID算式中的积分、微分运算只能用数值计算方法逼近，只要采样周期T_s取得足够小，这种逼近可以相当精确^[48]。本例中采样周期为3.3×10^-5s，可以满足精度要求。

将微分项用差分代替，积分项用矩形和式代替，则数字PID算式为

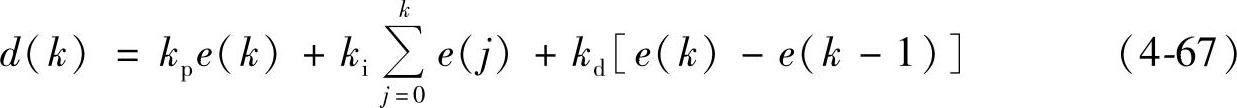
其中：k_p=K_p，k_i=K_pT_s/T_i，k_d=K_pT_d/T_s。

递推PID算式为：

d（k）=d（k-1）+q₀e（k）+q₁e（k-1）+q₂e（k-2） （4-68）

其中：q₀=k_p+k_i+k_d，q₁=-k_p-2k_d，q₂=k_d。

经计算得：q₀=77.27，q₁=-144.54，q₂=67.27，则有

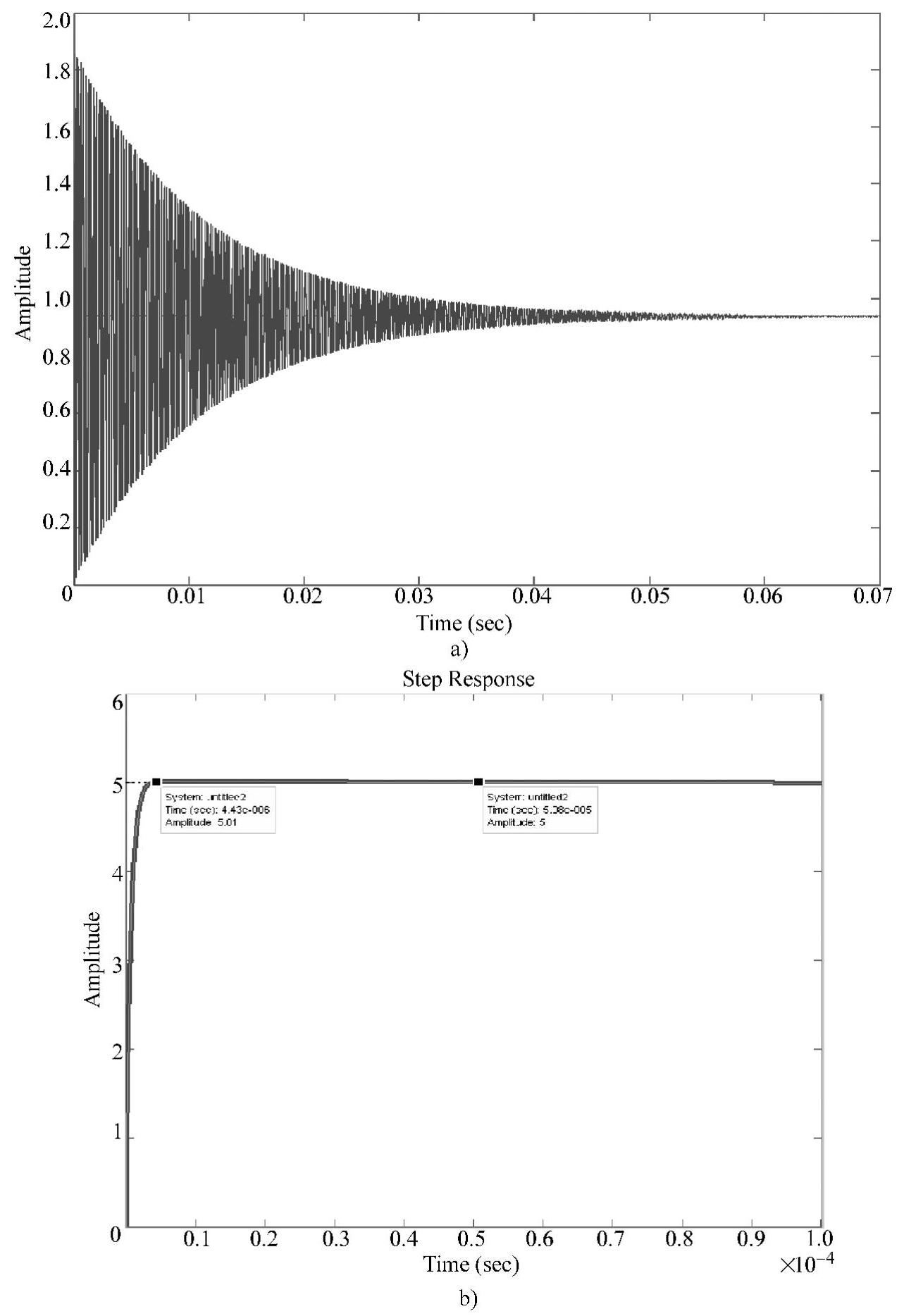
图4-108 系统闭环阶跃响应

a）未加PID控制 b）加入PID控制

d（k）=d（k-1）+77.27e（k）-144.54e（k-1）+67.27e（k-2） （4-69）数字PID的编程算式为：

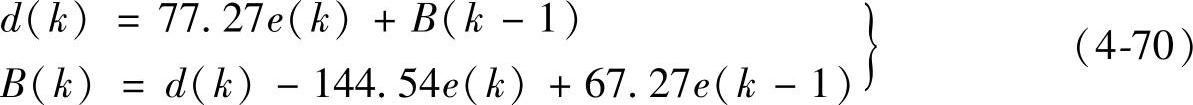
其中，d（k-1）是上一周期的占空比，e（k）是此次周期的误差，e（k-1）是上一周期的误差，e（k-2）前两次周期的误差。式（4-70）是计算机可编程实现的表达式，这样的算式可以使计算机运算延时时间最短^[48]。

综上所述，运用仿真工具，通过仿真分析，可得到被控对象的时域特性和频域特性，为对系统进行稳态、动态特性分析提供了直观的数据，用简单编程，在仿真环境下确定选取PID控制器参数是一种行之有效的方法，相对于传统的经验设计方法，提高了控制系统的设计效率。