数字控制是高频功率开关变换器控制技术的发展方向，目前已成为人们研究的热点之一。下面讨论用根轨迹技术为Buck变换器设计数字控制器。

首先要用相应的零极点映射方法将基于变换器的小信号模型转换成离散时间模型，其次将数字控制器的零、极点和增益设置在希望的闭环极点位置上，建立控制器的离散模型，然后将控制器的离散模型转化成差分方程，再用DSP芯片实现数字控制。具体设计步骤如下所述。

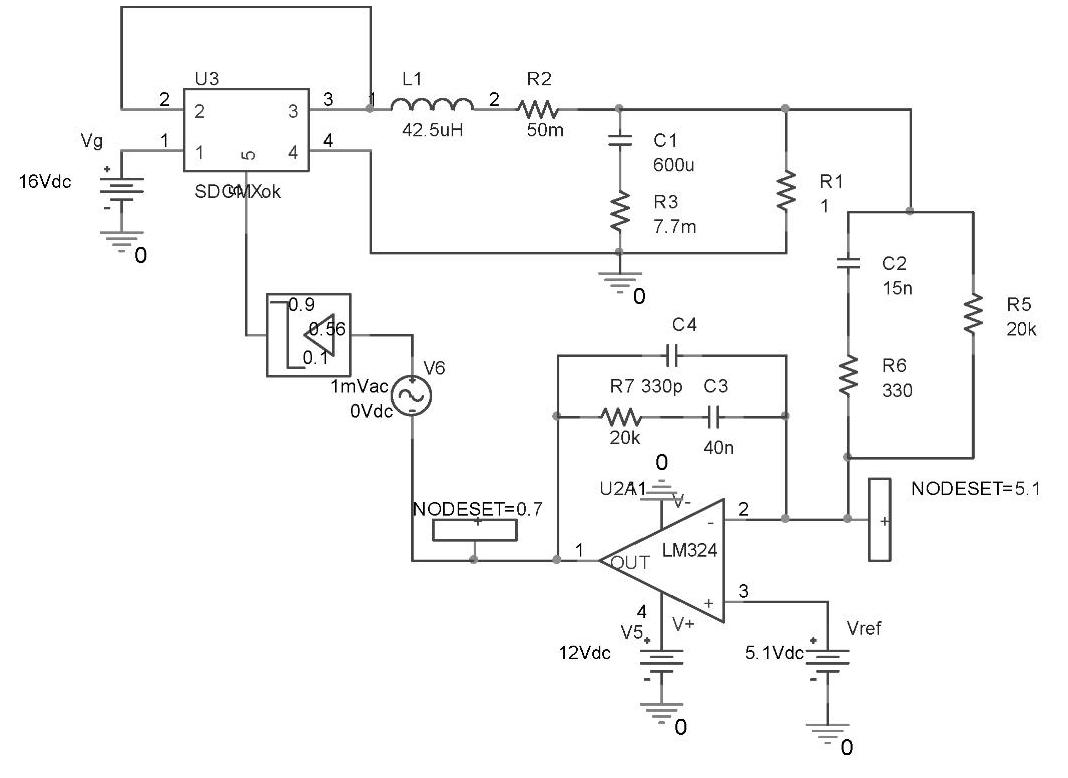
图4-87 用PSpice仿真T（s）的模型

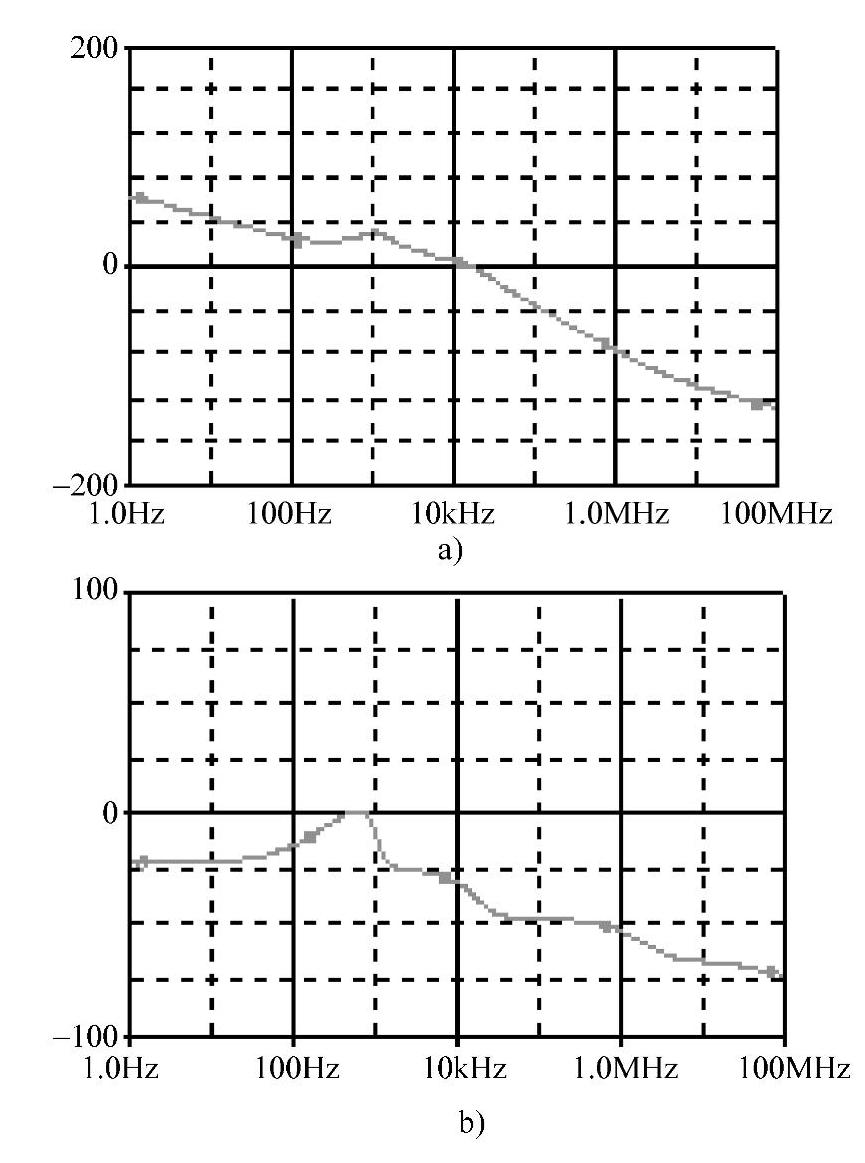
图4-88 用PSpice仿真的T（s）特性

a）幅频特性 b）相频特性

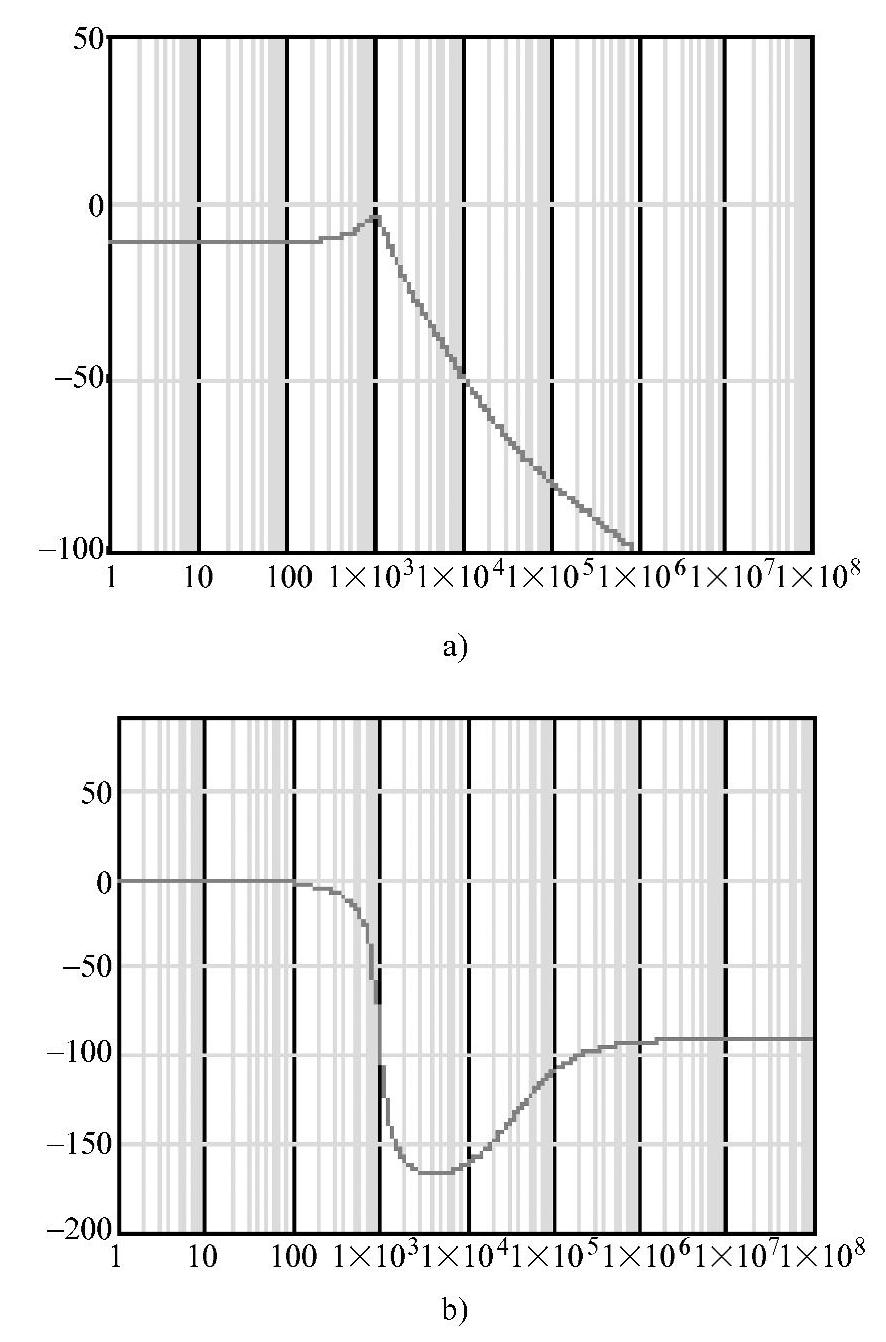
图4-89 Mathcad仿真音频传递函数的幅相频率特性

a）幅频特性 b）相频特性

步骤1：建立z-平面模型和画根轨迹

已知Buck变换器的小信号模型为：

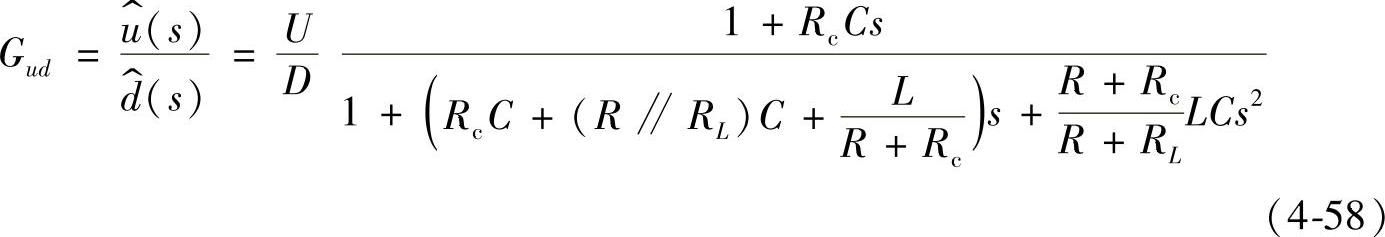
设Buck变换器及其各元器件参数条件同上，则可用相应的零极点影射方法将小信号模型转换成离散时间模型。根据z=e^sT的关系，将小信号模型的极点和零点映射到z平面。有限极点或零点在s=-a时，被映射到z=e^-aT，无穷极点或零点被映射到z=-1。采样周期T为20μs。为此Buck变换器的离散时间模型式（4-59）中，离散时间模型的零点为-0.3588，极点为0.9647±0.1182i。其模型的根轨迹如图4-93所示。从图上可见，两个极点非常接近单位圆，导致系统非常接近临界稳定，必须用根轨迹设计方法调整。

步骤2：数字控制器的设计

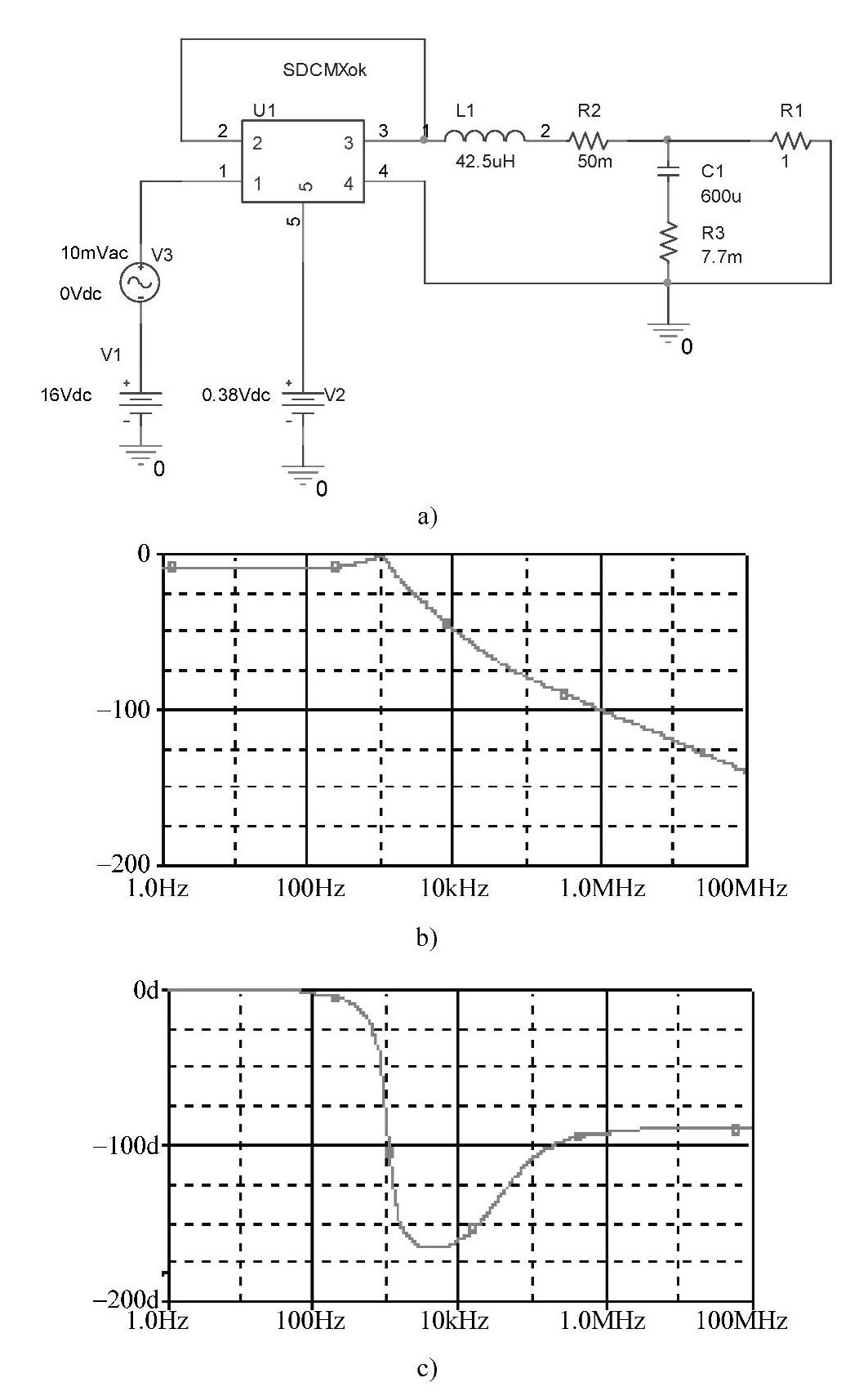
图4-90 用PSpice软件仿真音频传递函数的仿真模型和特性

a）仿真模型 b）幅频特性 c）相频特性

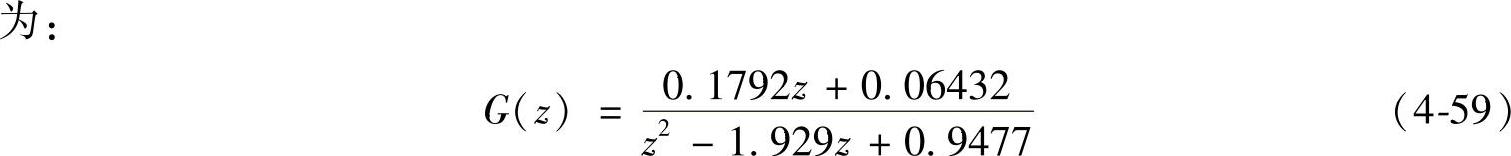
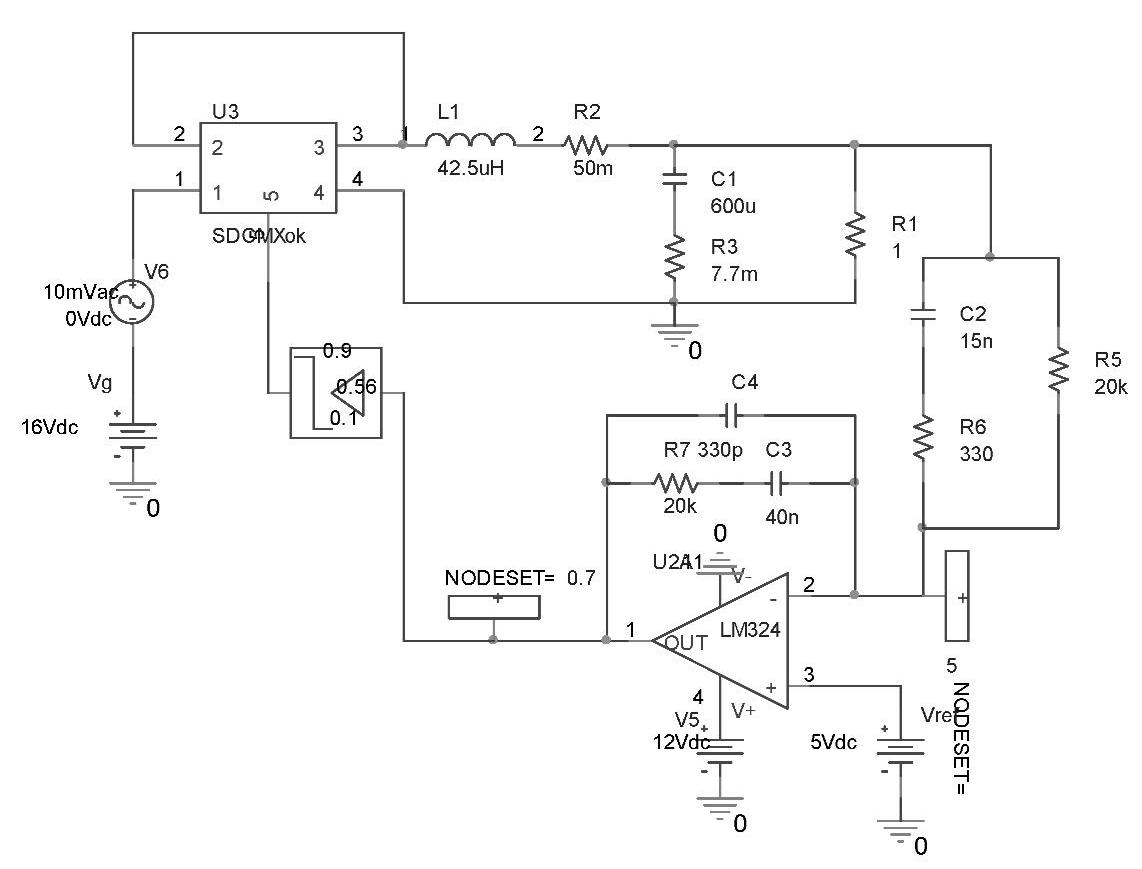
图4-91 用PSpice软件仿真闭环音频特性的仿真模型(www.daowen.com)

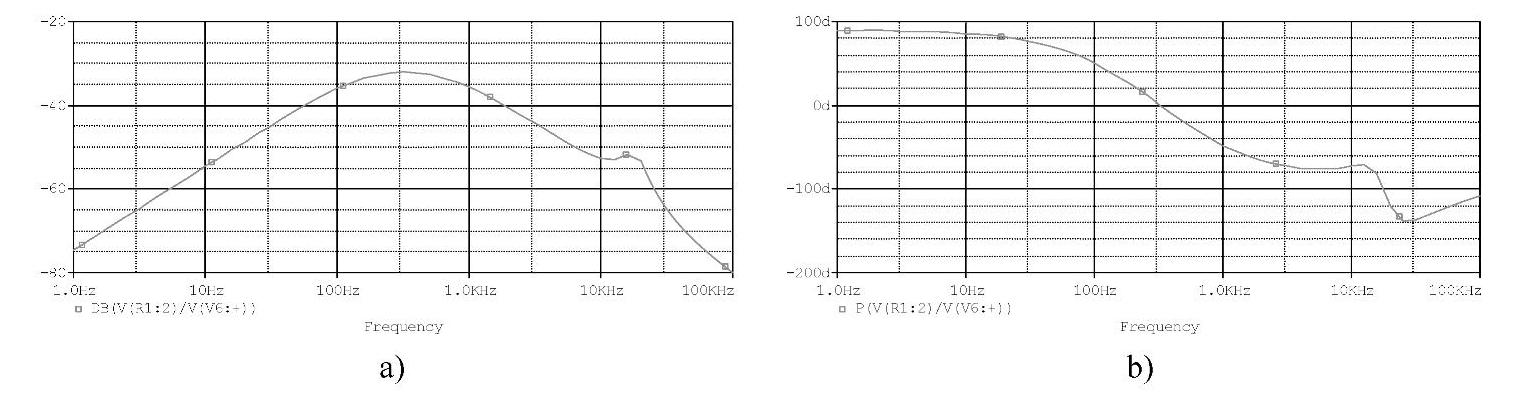
图4-92 用PSpice软件仿真闭环特性

a）幅频特性 b）相频特性

根据式（4-59）z-平面模型和如图4-93所示根轨迹图对Buck变换器可进行数字控制器的设计。将控制器的三个极点设置在实轴上，分别为0和10⁵×（-1.3247±1.1426i），将控制器的两个零点被分别设置在10³×（-1.8915±0.7646i）上。控制器的增益调整为5.4280，于是得到控制器模型的频率特性和根轨迹如图4-94、图4-95所示。由控制器的频率特性可看出，按根轨迹法配置控制器模型的特性与前述的控制器模型特性完全相同，因此控制器也将起到相同的补偿作用。

将控制器与Buck变换器的离散模型传递函数相乘，得到校正后Buck变换器的开环传递函数，引入负反馈后即可实现系统的闭环，利用Matlab进行计算，得到闭环的极点为0.9608+0.0087i，0.9608-0.0087i，-0.2381+0.1862i，-0.2381-0.1862i，和0.0560。闭环系统的频率特性与根轨迹如图4-96、图4-97所示。由图4-96可以看出，对于控制-输出的Buck变换器，其闭环模型频率特性与前面所述的输入-输出闭环特性相似，只差一个系数，由此可以证明根据零极点配置得到的控制器起到了相同的作用，可获得相同的结果。由图4-97可知，由于所有闭环极点完全位于单位圆内，保证了系统的稳定性。

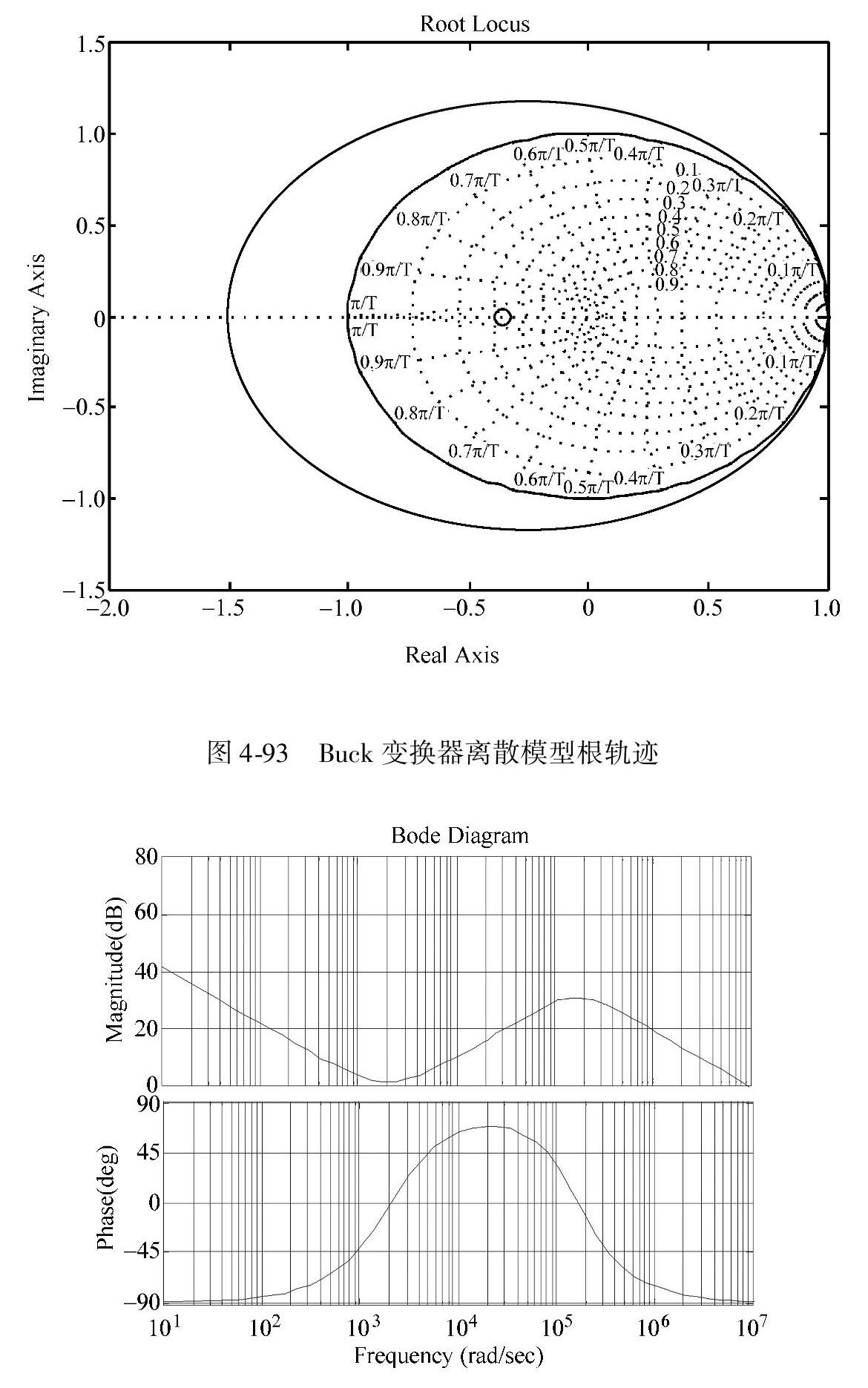
图4-94 控制器的频率特性

步骤3：求占空比计算式

控制器的传递函数为

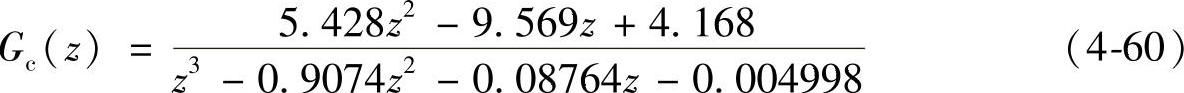
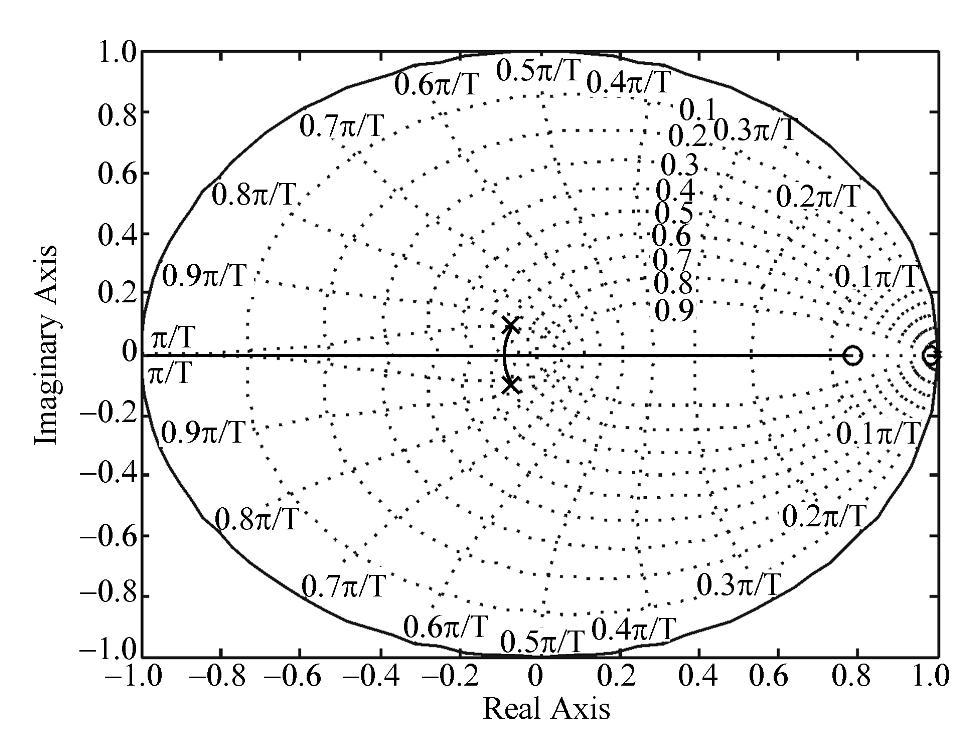
图4-95 控制器离散模型的根轨迹

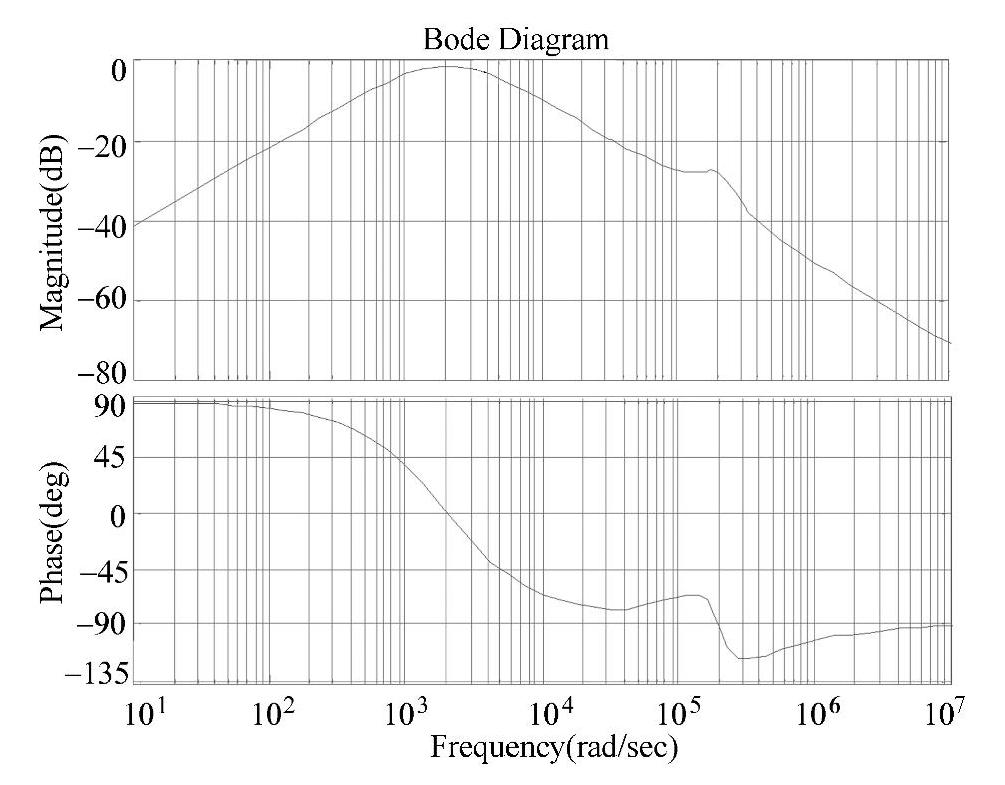
图4-96 闭环系统的频率特性

将式（4-60）所示的数字控制器的传递函数转换成差分方程[48]，可用于计算新的占空比。因此，占空比计算式为：

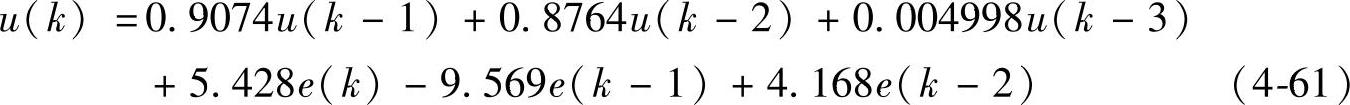
在式（4-61）差分方程中，u（k）是基于第k次采样的控制器输出，e（k）是基于第k次采样的误差输出。根据式（4-61）可编写占空比计算程序，利用TI公司的TMS320F2000系列DSP实现电压型开关调节系统的数字控制。

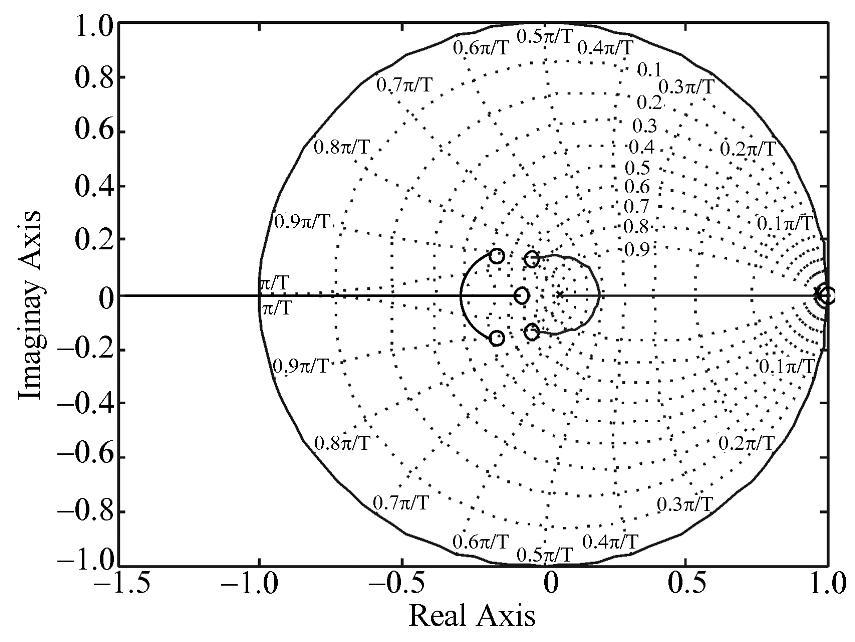
图4-97 校正后闭环系统的根轨迹