综合是与分析相反的命题^[46]。从控制观点出发，用数学方法寻找一个能满足技术要求的控制系统，通常把这项工作称为系统的综合问题。开关调节系统的复频域综合即是按开关变换器规定的性能构造、在复频域中决定合理的系统结构和各环节的参数、或者按规定的性能确定校正装置型式和参数。

鉴于开关调节系统设计步骤，所谓综合就是根据主电路的数学模型，寻找设计一个控制作用（主要指设计控制器），使得在其作用下系统运行的行为满足所给出的期望性能指标。为了便于设计，定义除补偿网络和电压采样网络之外的环节为控制对象，把补偿网络和电压采样网络合并，并称之为电压控制器。

设计控制器的主要思路如下^[1]：

（1）将时域内的技术指标转化为相应的频域参数。对于开关调压系统，由于在时域内可以使用较为通用的测量仪器进行测量，测量方法相对简单，而且测量结果直观易懂，所以，开关调节系统的技术要求大部分是通过时域技术指标体现的；但较为流行的设计方法是以复频域参数为设计依据，在复频域内设计其控制器。因此，需要将时域内的技术指标转化为相应的复频域参数。

（2）在复频域内分析开关变换器主电路的典型传递函数，并画出相应的对数频率特性曲线。

（3）根据主电路的典型传递函数和复频域参数，设计能够与主电路相匹配且满足设计技术要求的控制器。

可见，开关调节系统是一种特殊的自动控制系统。下面将介绍电压控制型开关调节系统的控制器设计。

控制器的设计是在已知控制对象的数学模型基础上进行的。这里以Buck电路为例讨论CCM型电压控制器的设计，如图4-81所示，设Buck变换器及其各元件参数条件为：U_g=16V，U=5.1V，电感L=42.5μH，电感的等效电阻R_L=50mΩ；输入电容C=600μF，ESR电阻R_C=7.7mΩ，工作频率f_s=50kHz，负载电阻R=1Ω，电路工作在CCM。设计步骤如下：

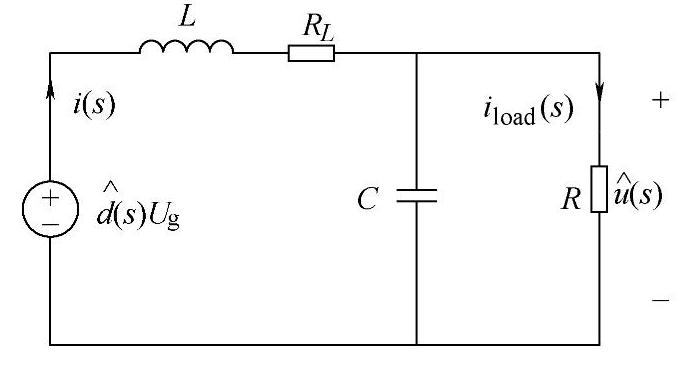
图4-81 考虑电感内阻的Buck变换器的等效电路

步骤1：设计电压采样网络。为了消除稳态误差，在低频段，开环传递函数的幅值远远大于1，即在直流频率点，系统为深度负反馈系统。对于深度负反馈系统，参考电压与输出电压之比等于电压采样网络的传递函数，即：

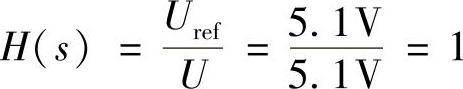
步骤2：绘制控制对象的博德图。对如图4-81所示的Buck电路，忽略电感电容等效串联电阻后其控制-输出的传递函数为：

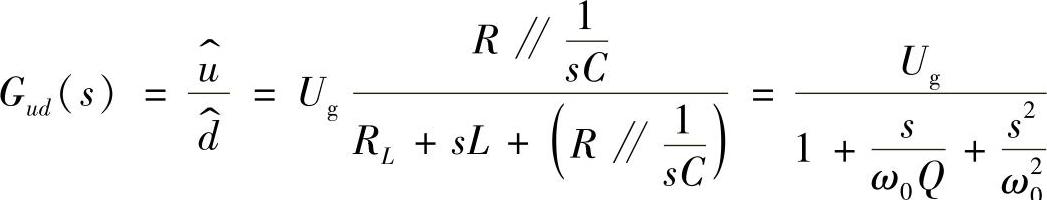
由ESR引起的零点参数为：

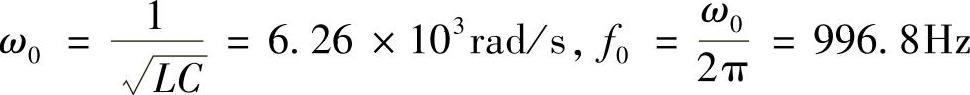
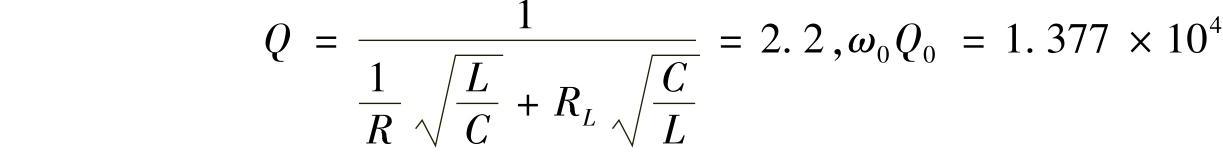
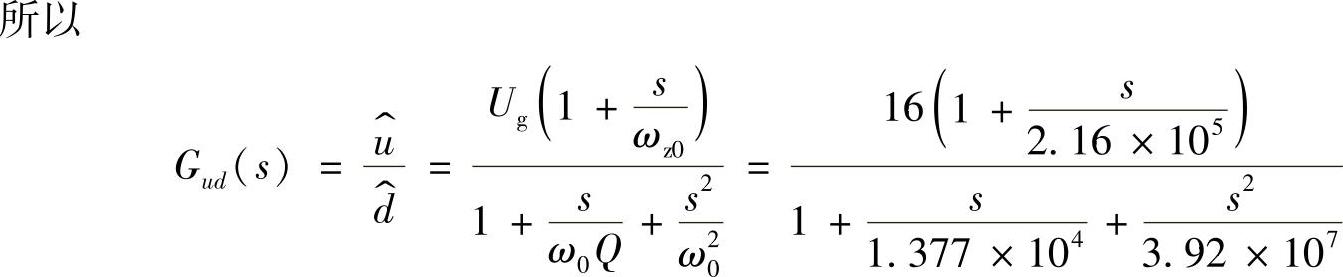
用PSpice软件仿真的模型和幅相频率特性如图4-82所示。也可用Mathcad仿真得到的控制-输出传递函数特性如图4-83所示。由图4-82和图4-83可见，两种方法仿真的特性完全一致。其中穿越频率f_c=4.1862kHz，相角裕量φ_m=180°-165.51°=13.49°＜45°。

步骤3：选择控制器。分析控制-输出传递函数特性并对照表2-1，选择双极点-双零点控制器如图4-84所示，其中电压U_ref=5.1V，U=5.1V。

双极点-双零点控制器的传递函数为：

步骤4：确定控制器的参数。

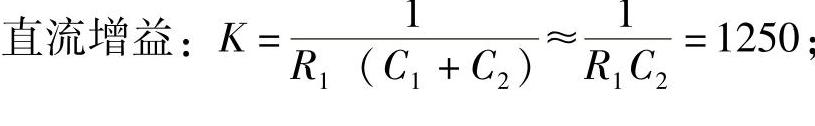
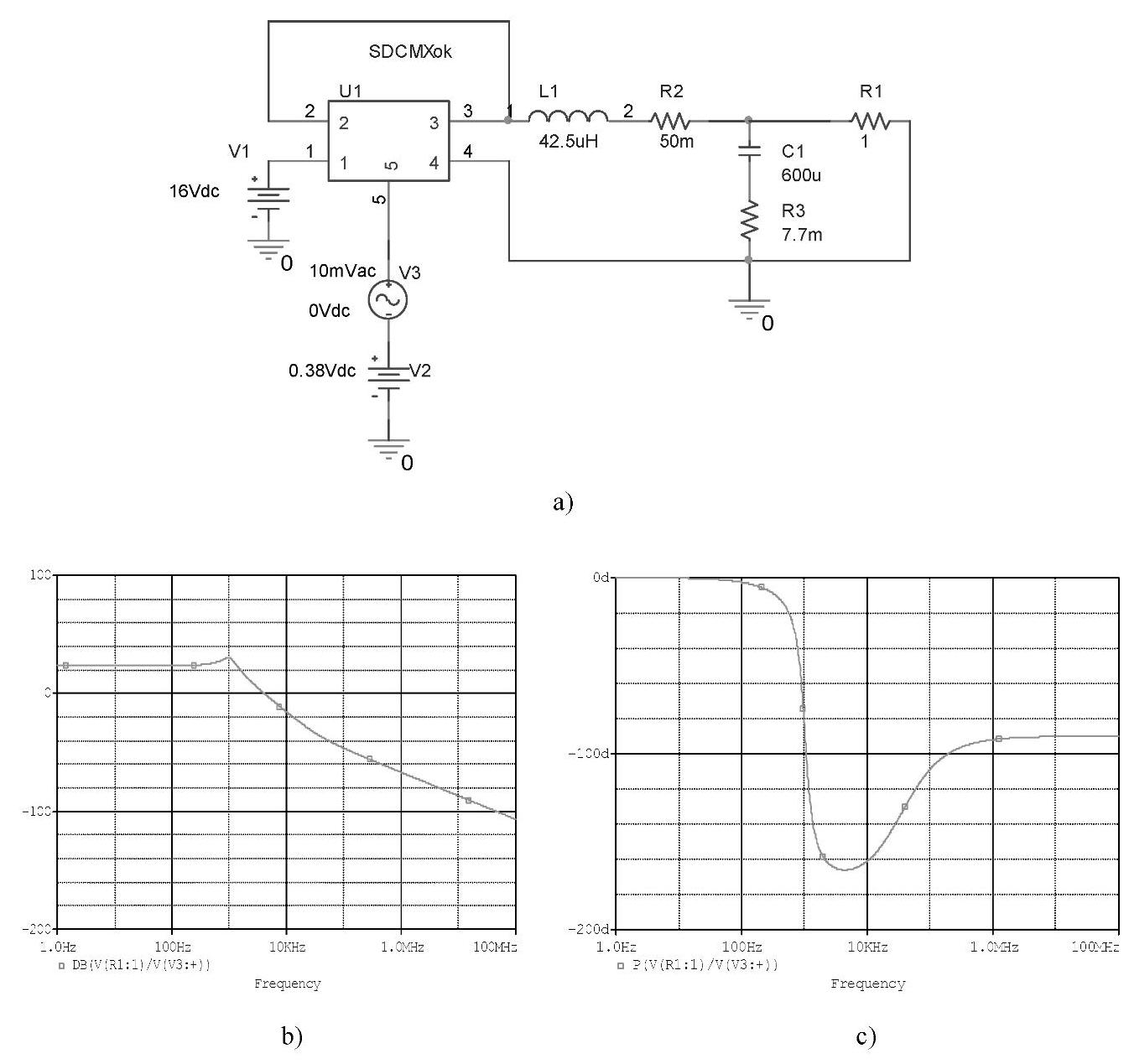
图4-82 用PSpice软件仿真控制-输出的传递函数(www.daowen.com)

a）仿真模型 b）幅频特性 c）相频特性

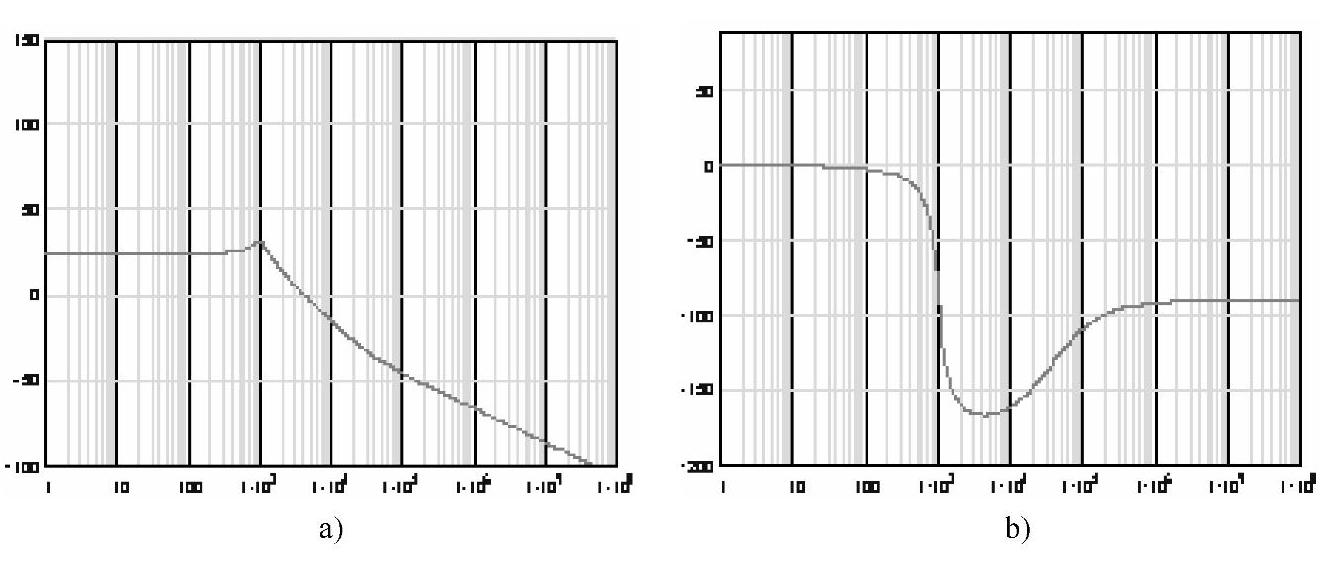
图4-83 用Mathcad软件仿真控制-输出的传递函数

a）幅频特性 b）相频特性

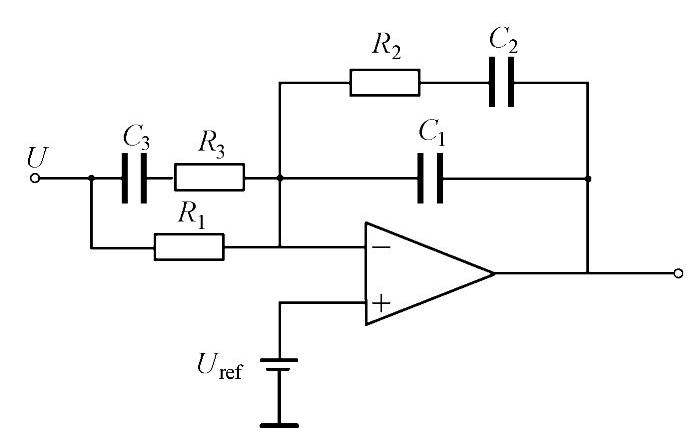
图4-84 双极点-双零点控制器电路

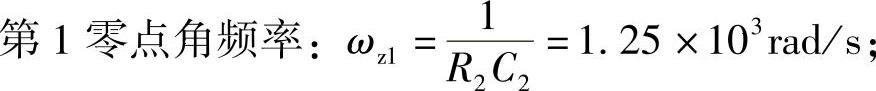
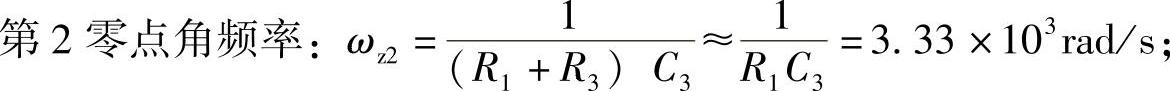
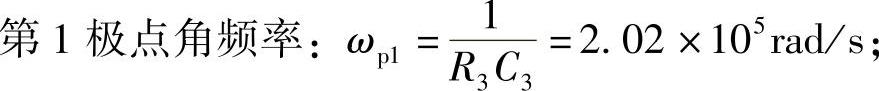
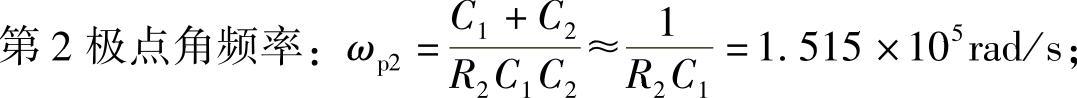
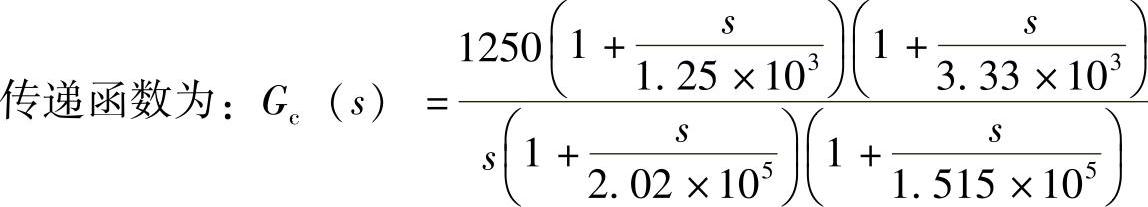
用Mathcad仿真控制器的幅相频率特性如图4-85所示。

步骤5：分析结果。控制器中的ω_z1，ω_z2用于抵消控制对象的极点，ω_p1用于抵消ESR引起的零点，ω_p2≥1.5ω_c，所以ω_c=10⁵ rad/s，f_c=15.9kHz，f_s/f_c=3.14，可见，穿越频率较高。

引入控制器后，系统开环传递函数为：

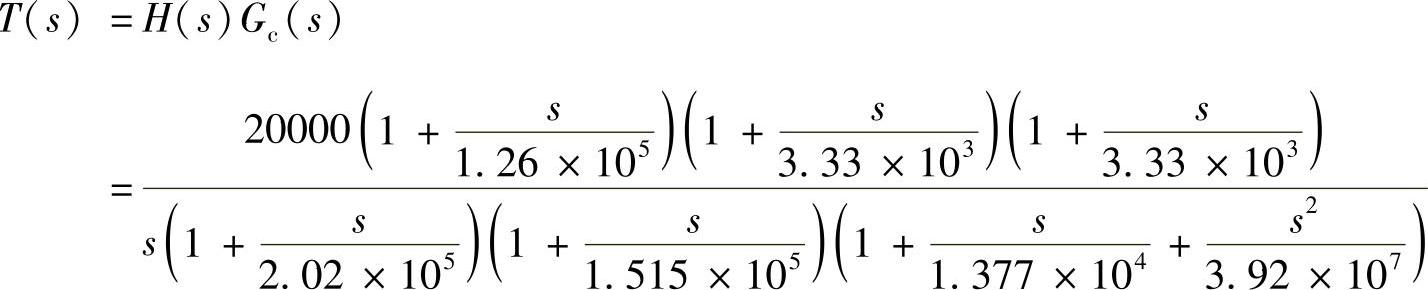
采用双极点-双零点控制器的电压控制开环幅相频率特性如图4-86所示，也可用PSpice软件进行仿真，其仿真模型如图4-87所示，特性如图4-88所示。其中20lg[（16×1250）/2π]=70.06dB，穿越频率f_c=21.969kHz，相角裕量φ_m=180°-134.18°=45.18°＞45°，可见，满足稳定性要求。

图4-85 控制器的传递函数的频率特性

a）幅频特性 b）相频特性

步骤6：反馈对音频的影响。未加反馈时音频传递函数为：

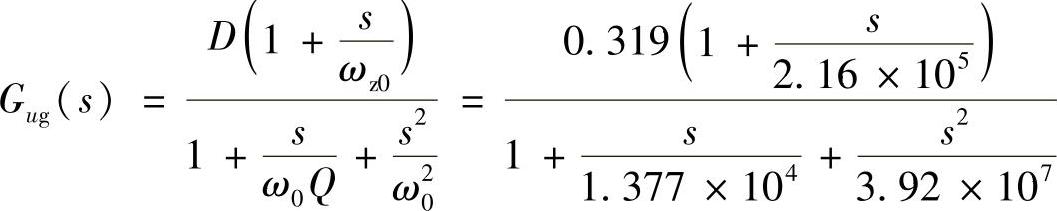
用Mathcad仿真输入-输出传递函数的幅相频率特性如图4-89所示，若用PSpice软件仿真音频传递函数，其仿真模型和特性如图4-90所示。引入补偿网络G_c（s）加了电压反馈后，闭环音频特性的PSpice仿真模型如图4-91所示，如图4-92所示为闭环音频特性。从开环和闭环特性可见，在100kHz处开环和闭环音频衰减率的幅值分别约为-10dB和-36dB，当输入电压U_g产生1V的波动时，输出电压U分别产生0.316V和15.8mV的变化。这个结果表明，电压反馈能够有效地减小输入波动对输出的影响。

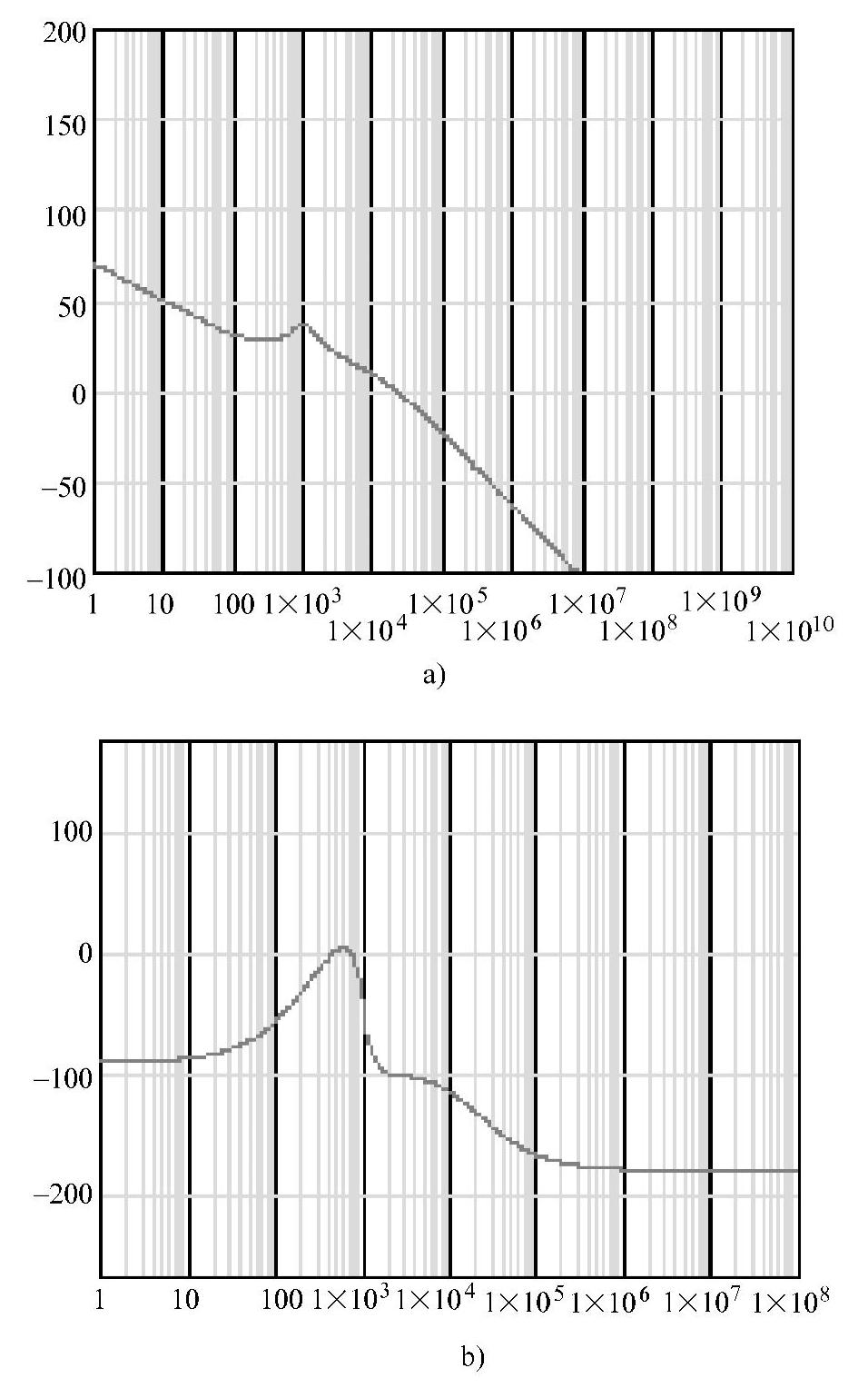
图4-86 具有控制器的开环传递函数波特图

a）幅频特性 b）相频特性