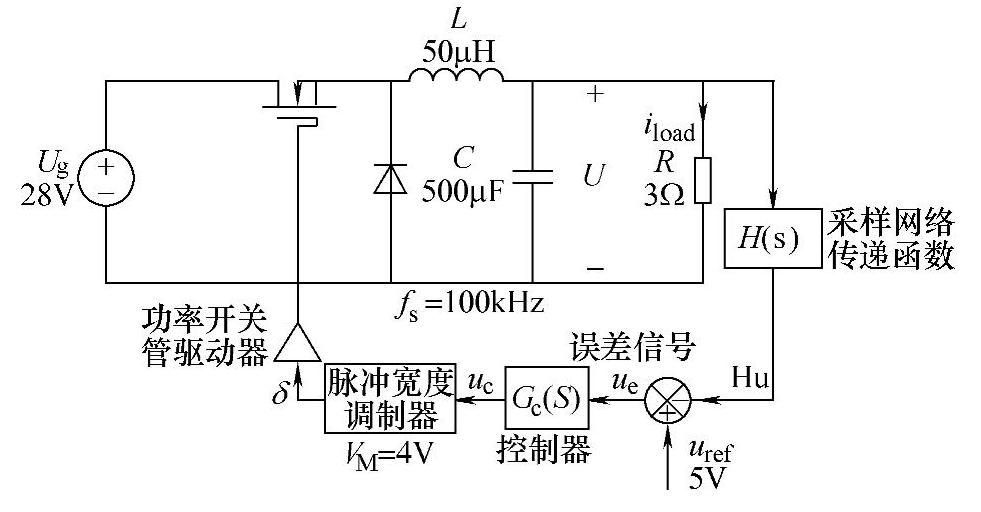
图4-56 例题中的Buck变换器电路

为了使读者对仿真技术在开关调节系统设计中的应用有更深刻地理解，这里结合对电压控制型开关调节系统的设计实例，介绍系统的性能仿真。

已知某Buck变换器及其各元件参数值如图4-56所示，图4-57给出了相应的交流等效小信号模型。其中系统输入额定电压U_g=28V，参考电压U_ref=5V，输出电压U=15V，负载R=3Ω，开关工作频率f_s=100kHz。PWM的锯齿波信号峰-峰值为V_M=4V。电路工作在CCM。要求设计反馈系统，使其能够满足稳态和动态要求。

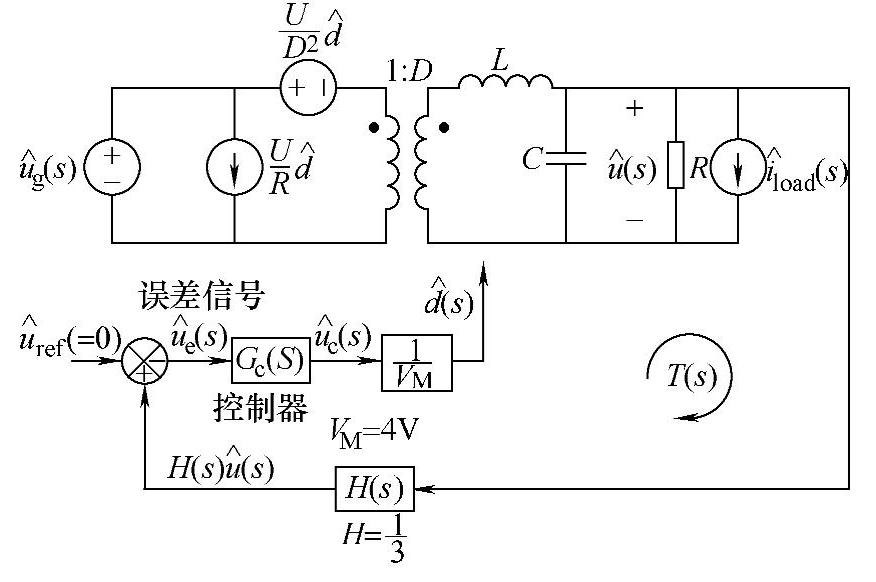
图4-57 例题中系统交流等效小信号模型

步骤1：按照本书第2章介绍的开关调节系统频域设计的一般步骤，首先要确定系统的控制方法，这里选用电压控制。

步骤2：绘制控制对象频率特性。可以通过Buck变换器的控制-输出传递函数，用Math-cad软件绘制，也可通过调用CCM1子电路模型，用OrCAD/PSpice软件仿真获取。用Or-CAD/PSpice软件仿真电路和Buck变换器G_ud（f）如图4-58和图4-59所示。

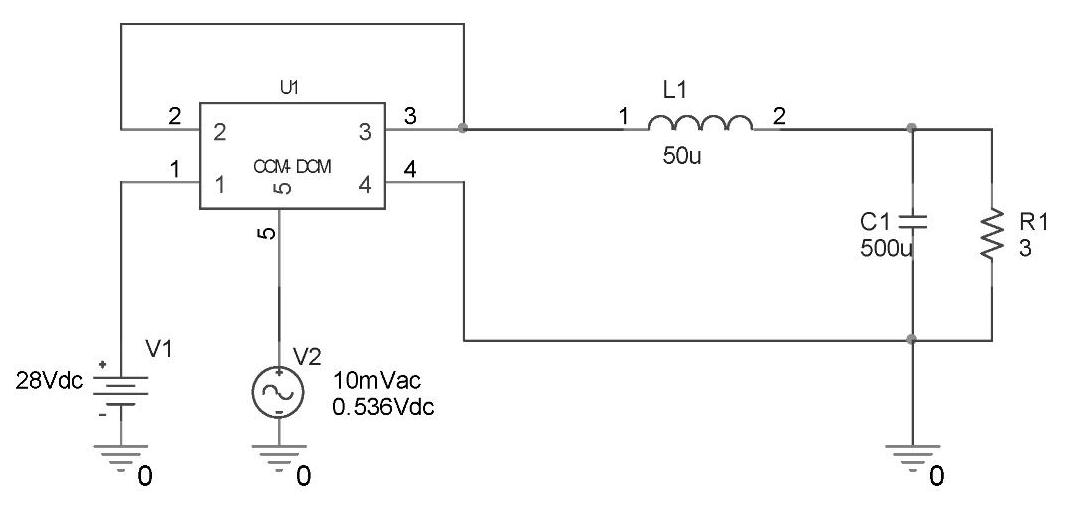
图4-58 例题中Buck变换器控制-输出传递函数的仿真电路

CCM型Buck变换器控制-输出传递函数表达式为

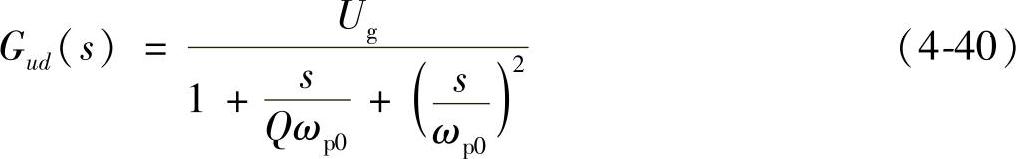
式中交流小信号模型中电路参数的计算值如下：

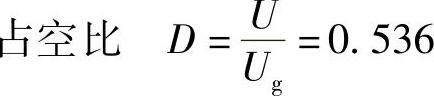
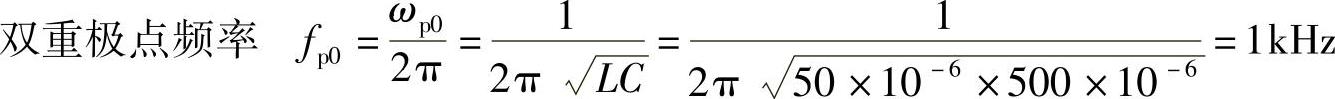
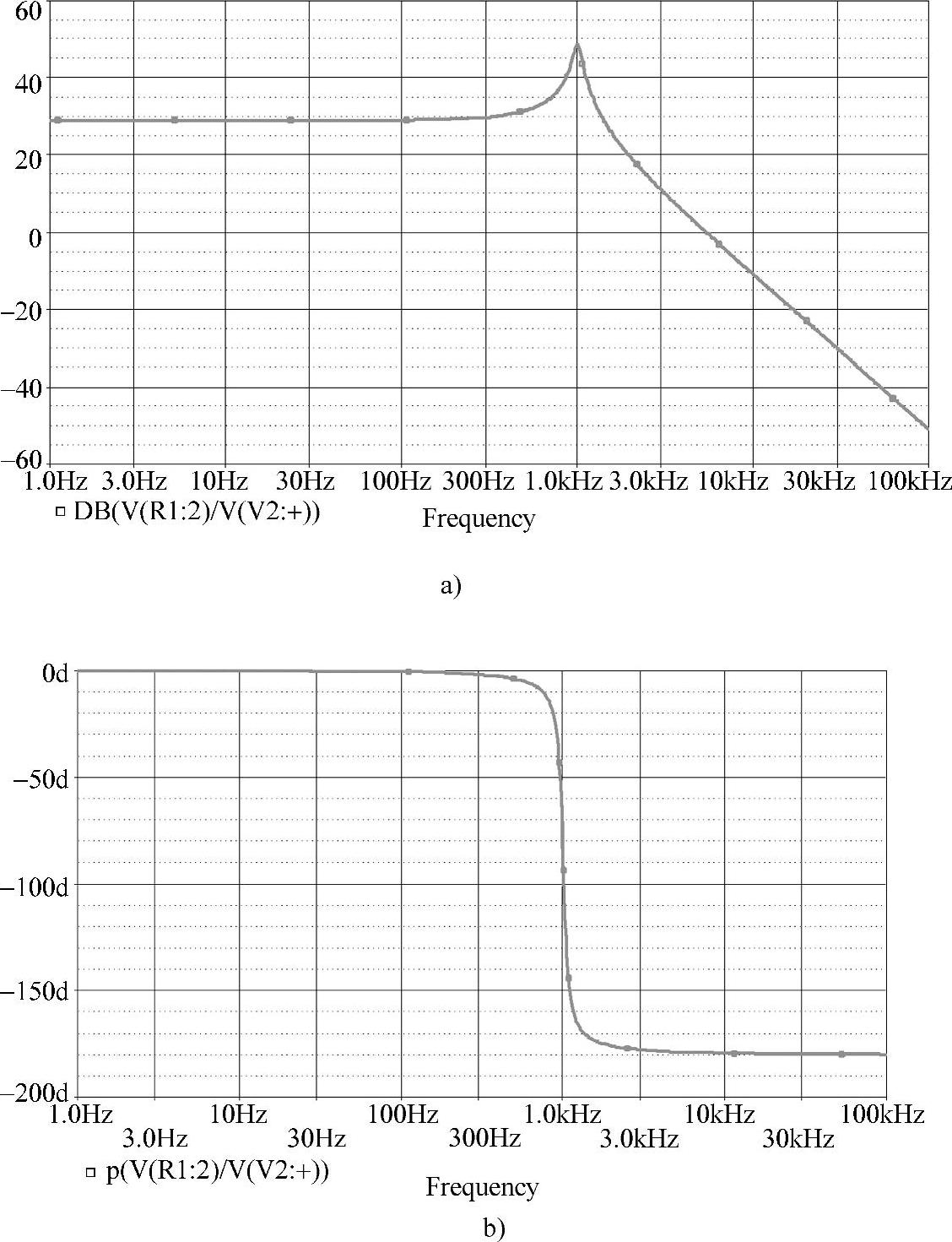
图4-59 例题中Buck变换器控制-输出传递函数的频率特性

a）幅频特性 b）相频特性

品质因数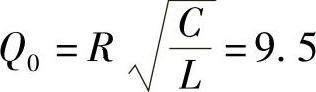，分贝表示为|Q₀|_dB=20lgQ₀=19.5dB

步骤3：绘制系统开环传递函数T（s）的特性。

如图4-57所示的系统，开环环路中含有电压采样网络，因此，先要设计电压采样网络。为了消除稳态误差，在直流频率点处系统应为深度负反馈系统，所以，电压采样网络的传递函数应为参考电压与输出电压之比，即

由图4-57可见，系统的开环传递函数为

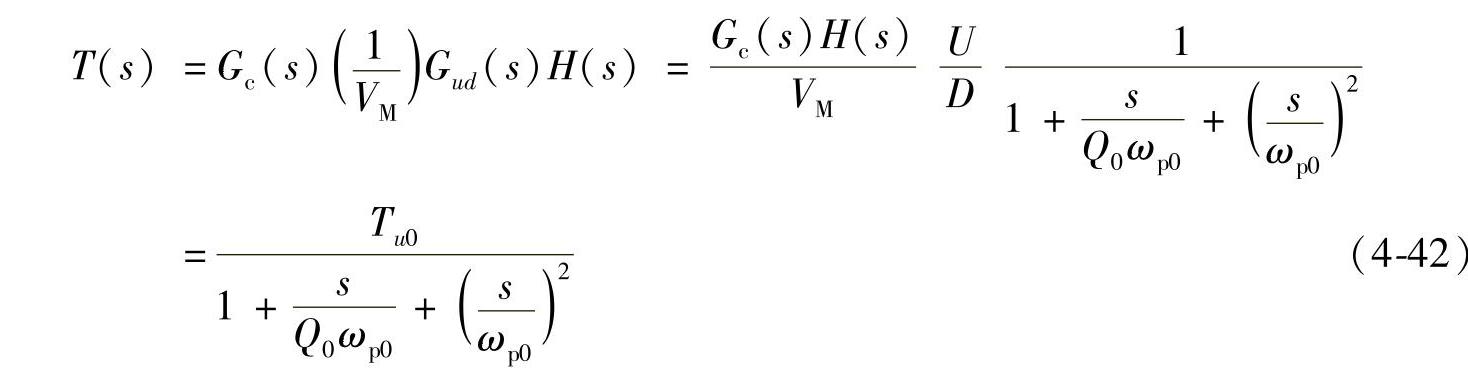
为了获得系统补偿前的开环特性，先假设补偿网络为G_c（s）=1，则直流增益为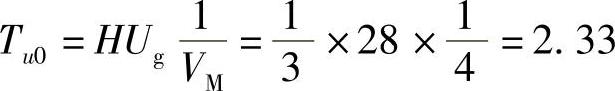，用分贝表示为|T_u0|_dB=20lgT_u0=7.4dB。系统的开环频率特性如图4-60所示，其中，穿越频率为f_c=1.827kHz，相位裕量φ_m=4.76°。从表面上看，系统是稳定的。但系统中的参数稍有变化，将会不稳定。由于直流增益T_u0=2.33，系统的稳态误差为1/（1+T_u0）=30%。另外，穿越频率太低，系统的响应速度很慢。以上这些指标都不符合设计要求，需要对其设计一合理的控制器，满足设计指标，使系统能稳定工作。

步骤4：选择补偿网络。

为了使加入补偿网络后，系统的开环传递函数的频率特性与本书第2章介绍的系统理想开环传递函数的频率特性（见图2-11）相似，选用PID补偿网络如图4-61所示，补偿网络的传递函数为

图4-60 系统开环传递函数频率特性

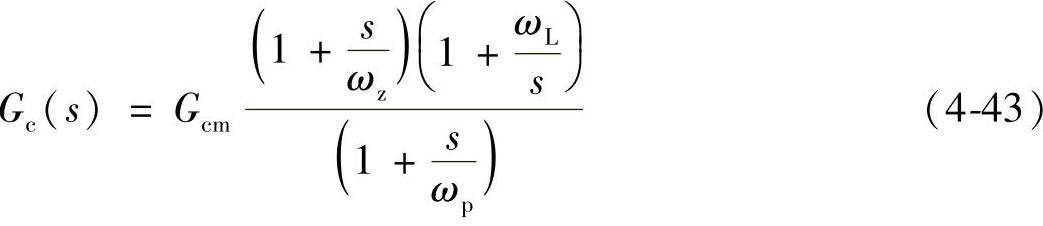
式中各参数计算表达式如下：

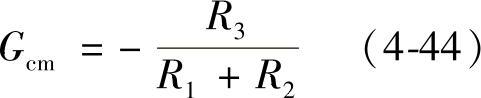
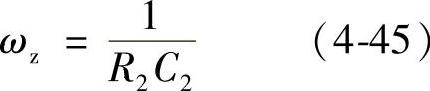
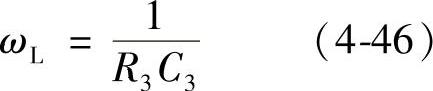
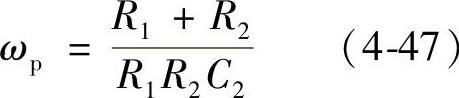
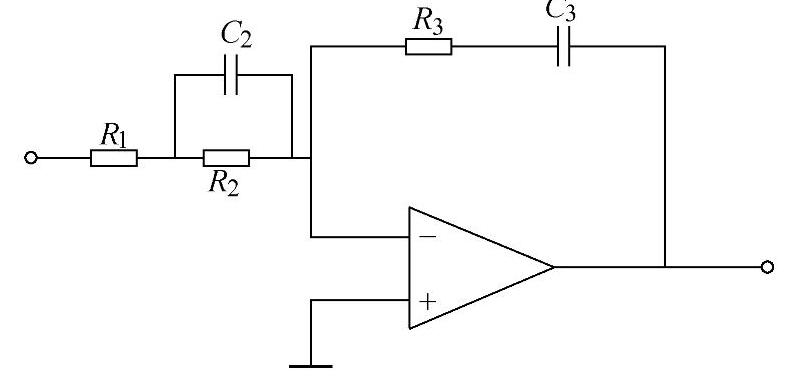
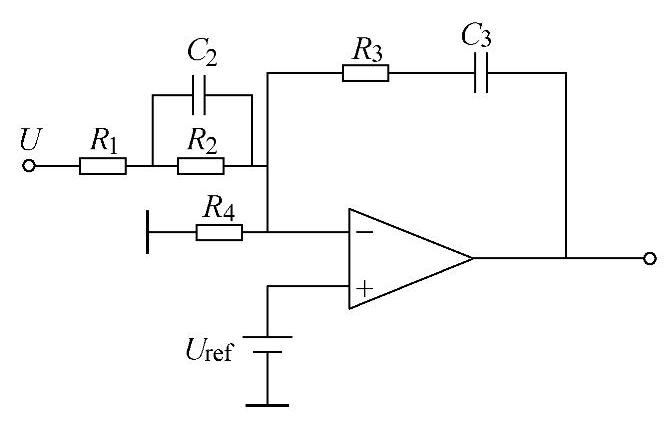
图4-61 PID补偿网络电路

步骤5：确定补偿网络参数。

为了提高穿越频率，设加入补偿网络后开环传递函数的穿越频率f_c是开关频率f_s的1/20，则穿越频率为

f_c=f_s/20=100kHz/20=5kHz （4-48）

PID补偿网络中有一倒置零点（1+ω_L/s），假设倒置零点的频率为穿越频率的1/10，而穿越频率设置在f_c=5kHz处，则有

又设相位裕量φ_m=52°，PID补偿网络的零、极点频率计算公式为^[33]

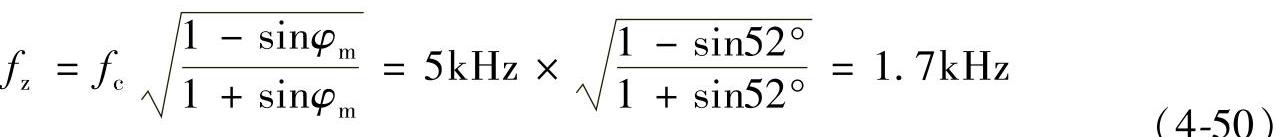
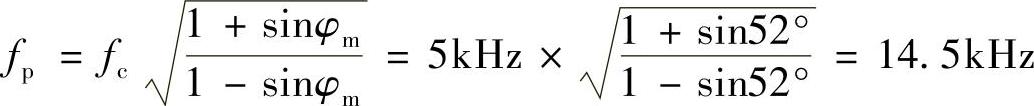
假设取C₂=1.1nF，由式（4-45）和式（4-50）可求得R₂=85kΩ；由式（4-47）和式（4-50）可求得R₁=11kΩ。采用PID补偿网络同时考虑采样网络的示意图如图4-62所示，此时，采样网络由下式确定：

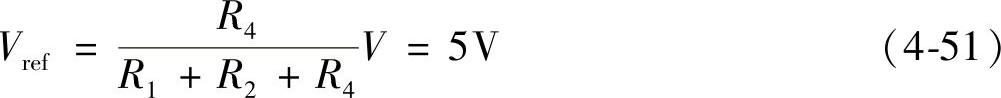
由式（4-51）可求得R₄=47kΩ。根据确定的补偿网络的参数，可得到补偿网络传递函数的幅频特性如图4-63所示。

(www.daowen.com)

图4-62 采样和补偿网络电路

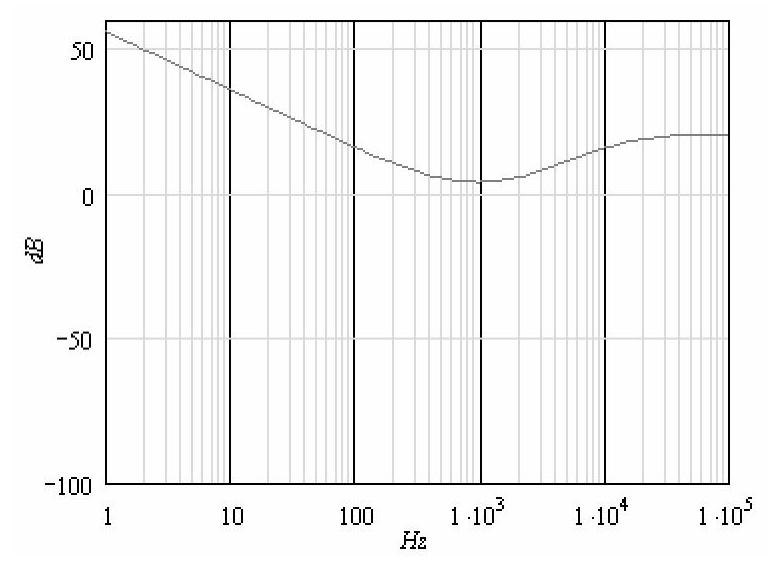
图4-63 PID补偿网络传递函数的幅频特性曲线

步骤6：补偿后系统开环传递函数频率特性仿真与设计分析。

基于Buck变换器电压控制型开关调节系统的仿真电路如图4-64所示，图中用组合型CCM/DCM模型代替开关网络；PWM调制器输出电压峰-峰值V_M=4V；用一个增益为0.25（=1/4）、含有最大、最小值限制行为的电压源模型E_PWM代替PWM调制器组成了其PSpice仿真模型，E_PWM输出电压值为0.25倍的PWM输入电压V_x，且将其最小值限制在0.1V，最大值限制在0.9V，PWM调制器的输出为平均开关模型的输入信号，即占空比d（t）。值得一提的是，在以上限制条件下开关的占空比可以在以下范围内取值：

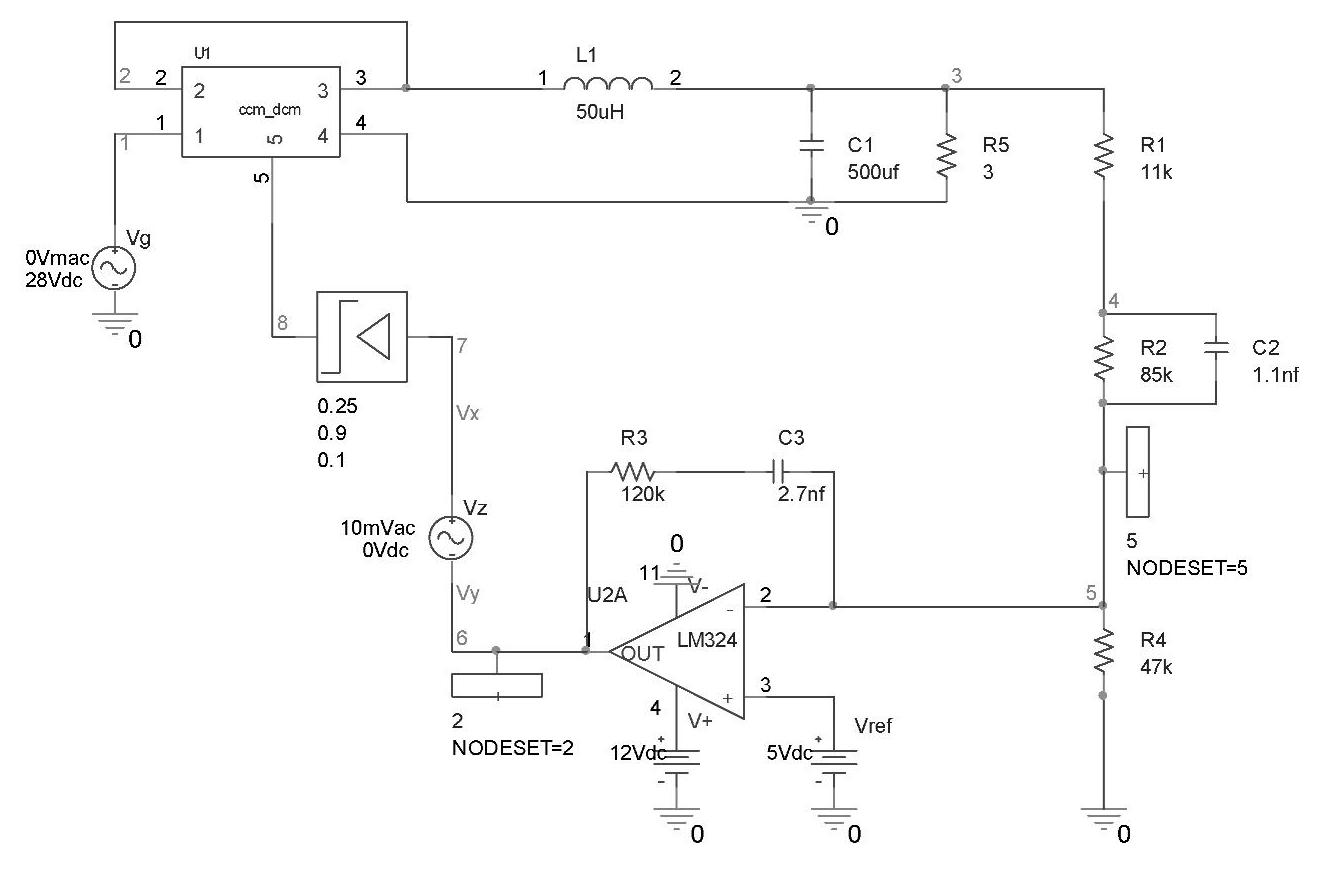
图4-64 基于Buck变换器的电压控制型开关调节系统频率特性仿真电路

D_min≤d（t）≤D_max （4-52）

由于E_PWM的限制作用，式（4-52）中，D_min=0.1，D_max=0.9。这是符合实际情况的，因为在实际PWM集成电路中，占空比最大值的限制条件为D_max≤1。所以引入模型E_PWM后，既可用于进行交流小信号分析，也可用于进行稳态分析。另外，由于此模型含有限幅功能，也可用于进行大信号扰动的分析。

用如图4-64所示的仿真电路可仿真获得如图4-65所示的基于Buck变换器电压控制型开关调节系统的补偿后的开环幅相频率特性。引入PID补偿网络后由仿真所得系统特性可见，低频段特性有一积分环节，因此系统稳态误差为零；中频段特性的穿越频率约f_c=5.27kHz，相位裕量约φ_m=47°，可同时满足系统快速性和稳定性要求；高频段特性以-40dB/dec的斜率下降，能够有效抑制高频干扰，因此，补偿网络设计合理，系统能够稳定工作，满足设计要求。

以上通过一个设计实例，详细介绍了在开关调节系统设计中仿真工具的应用。为了让读者能更好地理解和掌握仿真技术，下面进一步分析如图4-64所示的仿真电路。

为了仿真获得系统的开环传递函数频率特性，需在电压控制器的输出端与PWM调制器的输入端之间插入一个交流小信号电压源V_z。由于运算放大器的输出阻抗非常小，而PWM调制器的输入阻抗非常大，选择这个位置施加小信号交流扰动电压源不会影响系统的开环传递函数频率特性。令交流小信号扰动电压源V_z的幅度为1mV，其值远远小于电压控制器的静态输出电压。在静态工作点的基础上，施以交流小信号扰动，通过AC扫描分析，得到系统的开环传递函数为

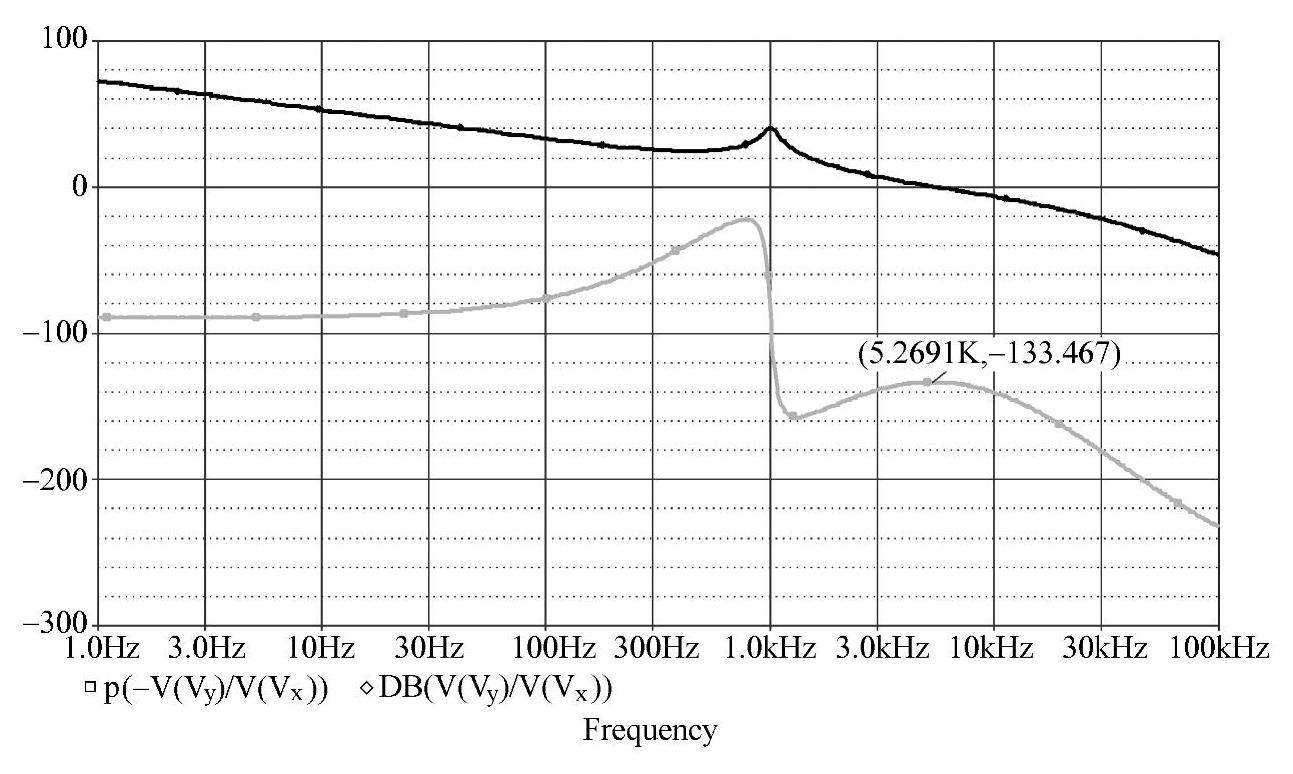
图4-65 例题中的开关调节系统幅相频率特性

在进行AC扫描分析之前，仿真软件的仿真器需计算出直流静态工作点，并在该静态工作点处对电路进行线性化，然后在指定的信号频率范围内进行AC分析，求取小信号频率响应。在求解静态工作点时，计算机要通过多次迭代对描述系统的非线性方程进行数值求解。在某些情况下，仿真过程中会出现不收敛现象且仿真出现异常中断问题，并给出错误信息，而对于具有很大直流环路增益的反馈系统，仿真过程中经常会出现不收敛现象。本例题中的开关调节系统正是具有很大直流环路增益的反馈系统，因此，需要对仿真电路进行事先处理，否则很有可能出现不收敛现象而导致仿真失败。解决的方法是用NODESET器件把节点电压初值指定为近似值或期望值，使非线性方程的数值求解被设定为合理的初值，因而求解的结果被限定在初值的某个邻域内。这种解决方法具体应用到图4-64所示的电路时，应作如下处理：根据给定的参考电压数值，通过求解电压采样网络得知静态输出电压U接近15V，运算放大器反相输入端的电位近似等于参考电压（v（5）=5V），静态占空比近似为D=U/U_g=0.536。因此，PWM调制器的输出电压v（8）=0.536V。在给定了这些近似节点电压情况下，非线性方程数值解收敛。想要直接获得静态工作点的计算值，可在建立完仿真电路并运行后，点击操作界面上的“Enable Bias Voltage Display”按钮即可。系统在两种不同负载电阻值下，得到静态工作点计算结果如下：

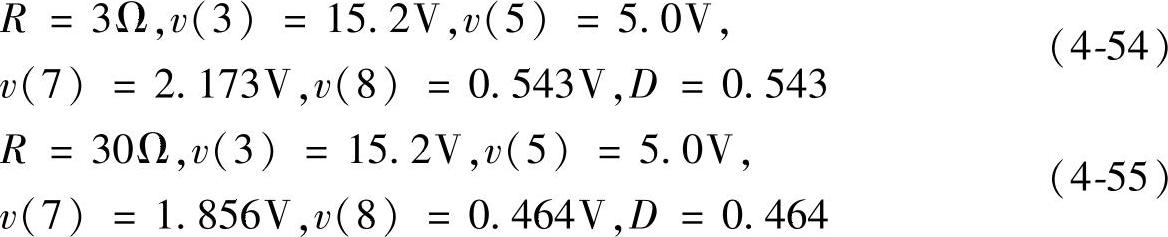
系统带载电阻R=3Ω时，Buck变换器运行在CCM下，其闭环频率特性如图4-65所示。系统带载电阻R=30Ω时，变换器运行在DCM模式下，其闭环频率特性如图4-66所示。两种模式下系统的开环传递函数的幅相频率特性如图4-67所示。由特性可知，①当R=3Ω时，截止频率f_c=5.3kHz，相位裕量φ_m=47°；②当R=30Ω时，截止频率降到f_c=371Hz，相位裕量增加到φ_m=53°。可见，变换器工作在CCM和DCM时，它们的环路增益频率响应差别较大。

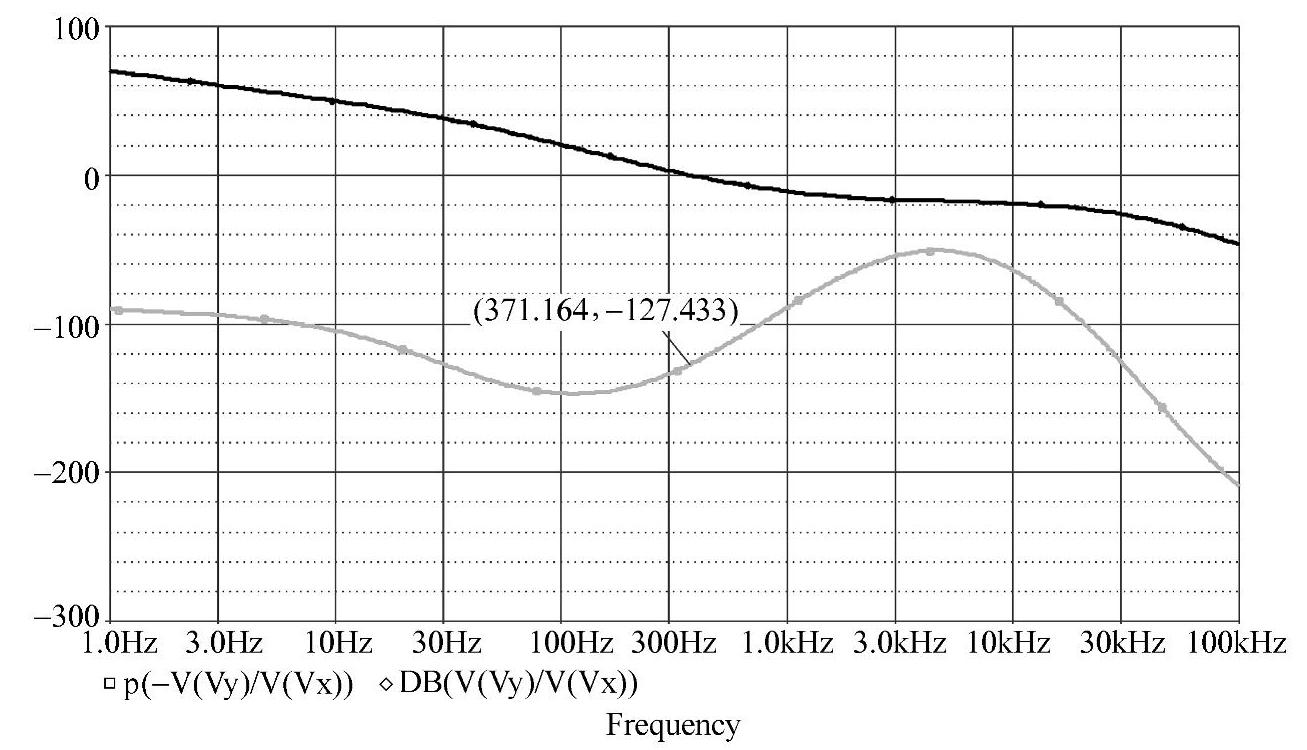
图4-66 R=30Ω时例题中的开关调节系统幅相频率特性曲线

开关调节系统的输入-输出传递函数的频率特性（音频衰减率）是另一研究系统的重要特性。系统反馈后对音频衰减率的影响程度是下面要讨论的问题。

系统开环运行时仿真电路如图4-68所示，图中在CCM/DCM器件的端口5处施加了一个直流电压源，其值设为静态占空比D=0.543。仿真不同负载下的开环和闭环音频衰减率的幅频特性如图4-69所示。

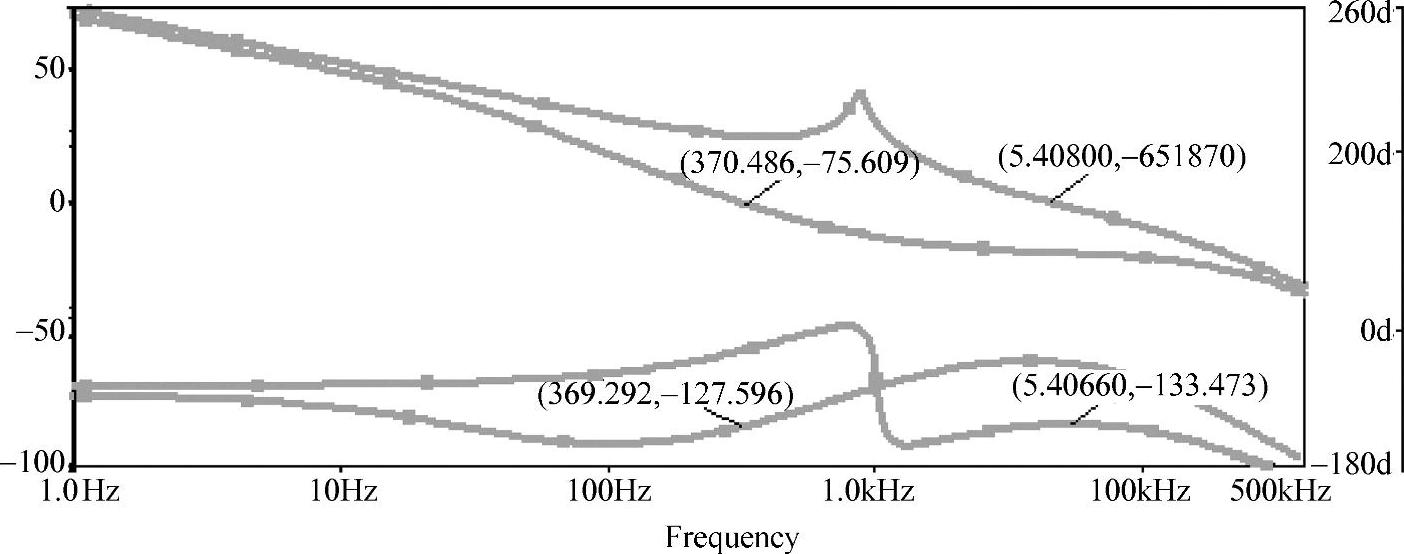
图4-67 CCM和DCM下Buck变换器电压控制型调节系统的频率特性

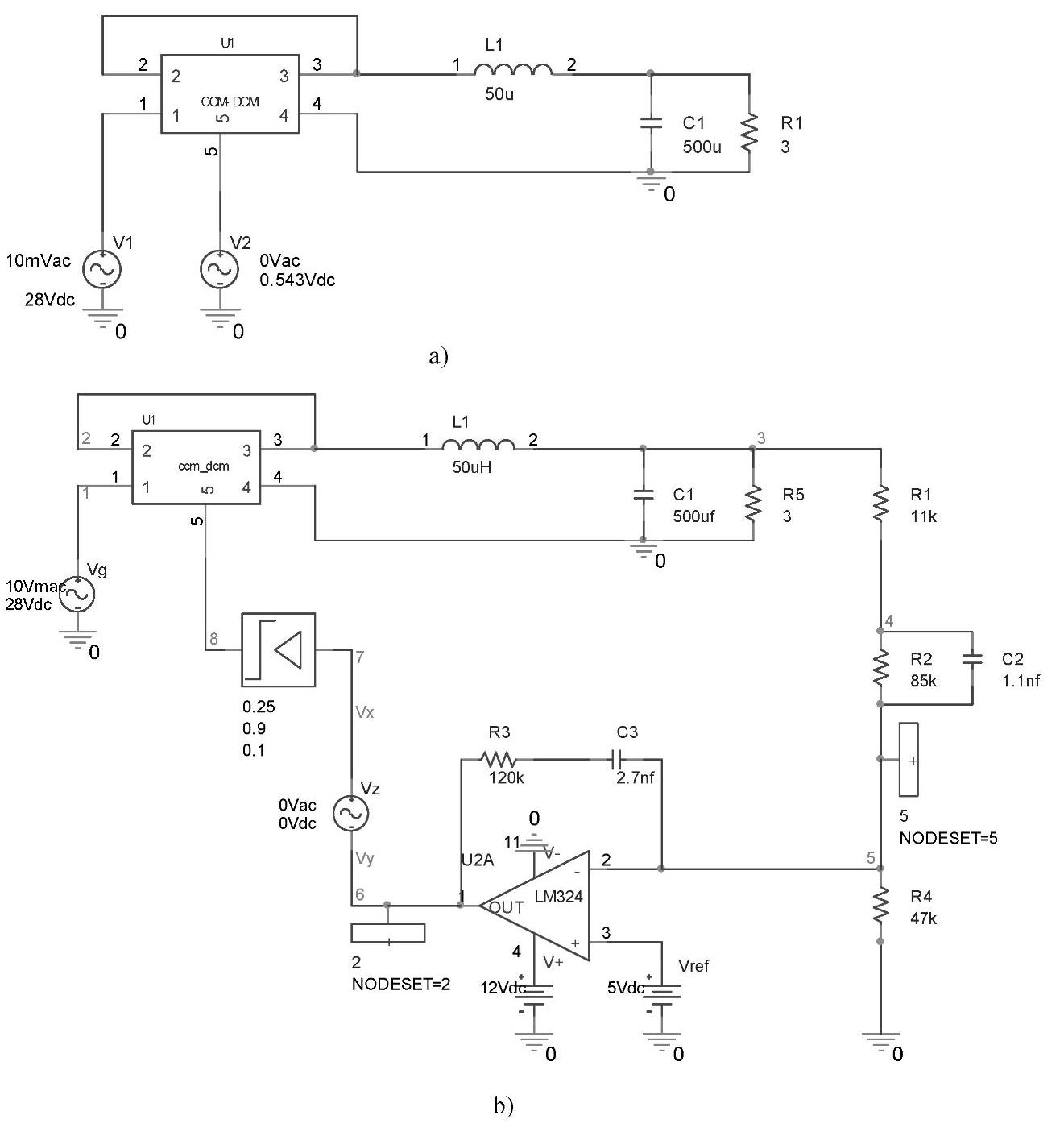
图4-68 电压控制型Buck调节系统音频衰减率仿真电路图

a）开环仿真电路 b）闭环仿真电路

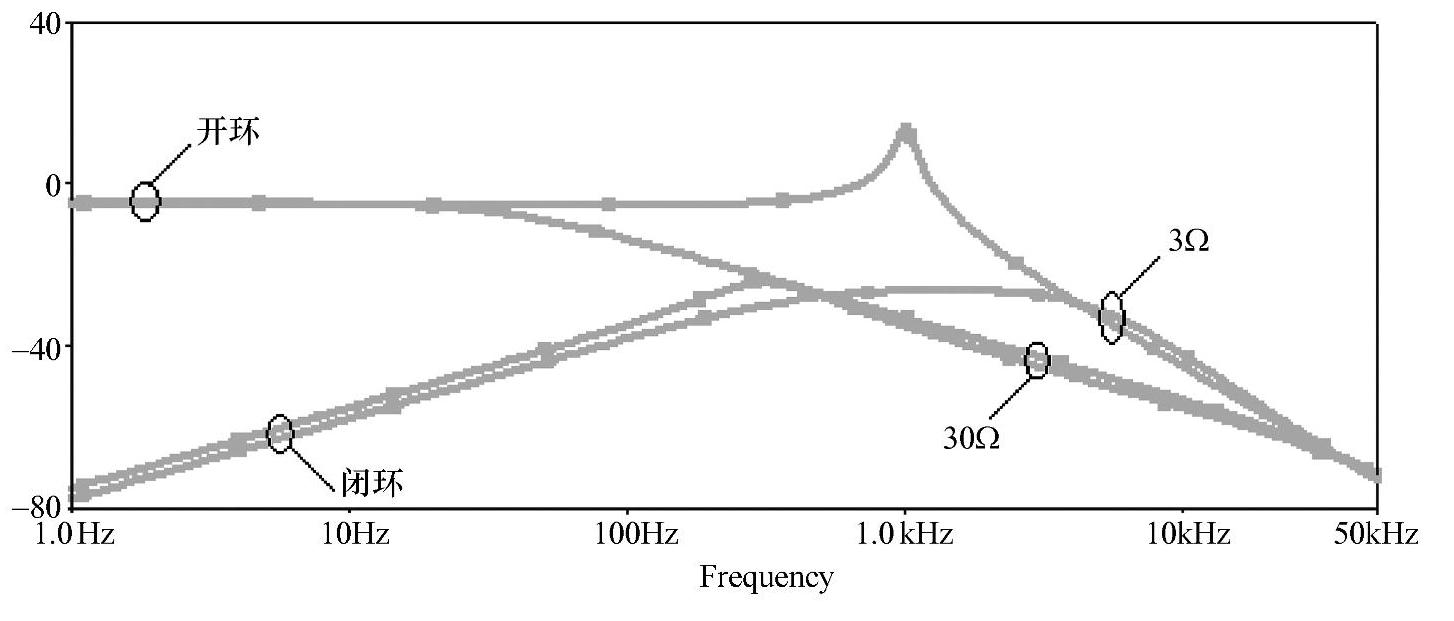
图4-69 电压控制型Buck调节系统音频衰减率幅频特性

讨论：

1）当负载R=3Ω时，系统运行在CCM下，由特性可见，在频率为100Hz处，开环和闭环音频衰减率的幅度分别-5dB和-38dB，如果设输入电压U_g产生1V的波动时，输出电压U分别有

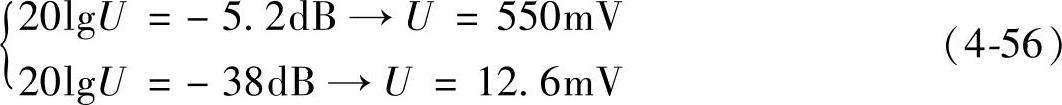
上式表明，输入电压有1V的波动，系统开环时在输出电压上产生550mV的变化；系统闭环时在输出电压上产生12.6mV的变化，说明电压反馈能够有效的减少输入波动对输出产生的影响。

2）当负载R=30Ω时，系统运行在DCM下，在频率为100Hz处，开环和闭环音频衰减率的幅度分别-14dB和-34dB，仍设输入电压U_g产生1V的波动，输出电压U分别有

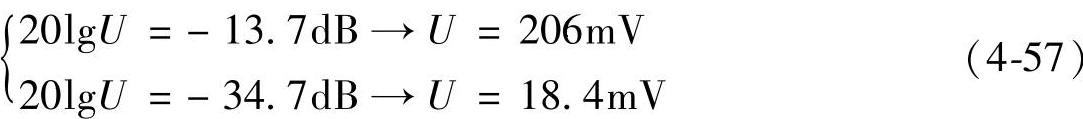
式（4-57）表明，输入电压有1V的波动，系统开环时在输出电压上产生206mV的变化；系统闭环时在输出电压上产生18.4mV的变化，说明电压反馈在DCM下也能够有效的减少输入波动对输出产生的影响。

3）综合1）和2）两种情况，在100Hz频率处输入电压U_g发生1V波动时，CCM下系统闭环时在输出电压上产生12.6mV的变化，DCM下系统闭环时在输出电压上产生18.4mV的变化，因此，系统在轻载运行时，反馈抑制电网电压波动的能力较之CCM差。

以上研究了电压控制型Buck开关调节系统小信号扰动下的特性，下面研究系统在大信号扰动下的瞬态响应。

如图4-70和图4-71所示分别给出了开环和闭环大信号仿真电路。两图中的开关器件U3和电阻R6组成了系统的定时加载电路，参数设置时，将开关器件U3的闭合时刻TCLOSE设为0.1ms，闭合时间TTRAN设为0.1ms，这样，在仿真时，U3开关在0.1ms处闭合，合闸的时间为0.1ms。

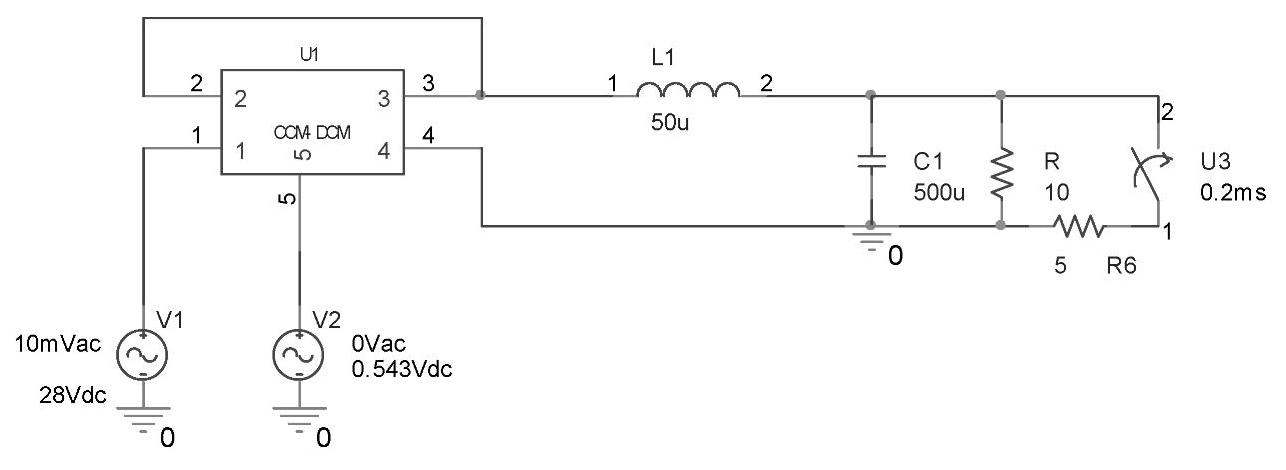
图4-70 Buck变换器开环瞬态响应仿真电路

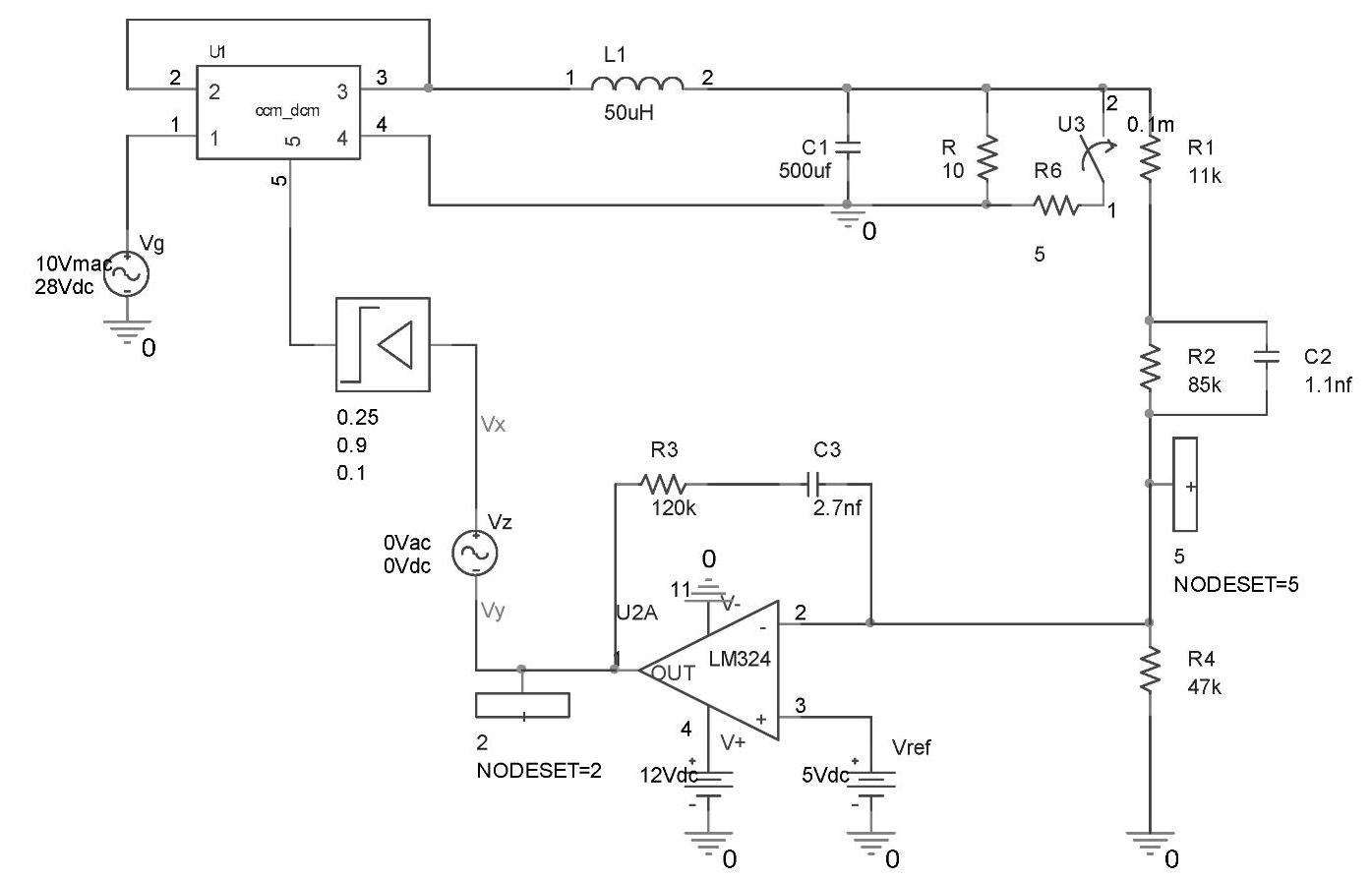
图4-71 电压控制型Buck调节系统瞬态响应仿真电路

如图4-72所示为突增负载时Buck调节系统开环和闭环瞬态响应特性，其中如图4-72a所示为负载电流瞬态响应，如图4-72b所示为输出电压瞬态响应。

从负载电流瞬态响应特性中可见，负载电流初值为1.5A，在0.1ms时刻突增负载，在0.2ms处，负载电流增加到新的稳态值4.5A。

系统开环时，且恒定占空比D=0.543，输出电压的瞬态响应是由变换器网络的时间常数决定的。在输出电压瞬态响应特性上可观察到一个长时间的弱阻尼振荡。而闭环控制时，电压控制器能动态地调节占空比来保持输出电压恒定。在开关闭合时刻，即突增负载时，输出电压出现一个幅度为0.2V负冲，而经过一个短暂的、强阻尼振动后，输出电压很快又会恢复为正常值。

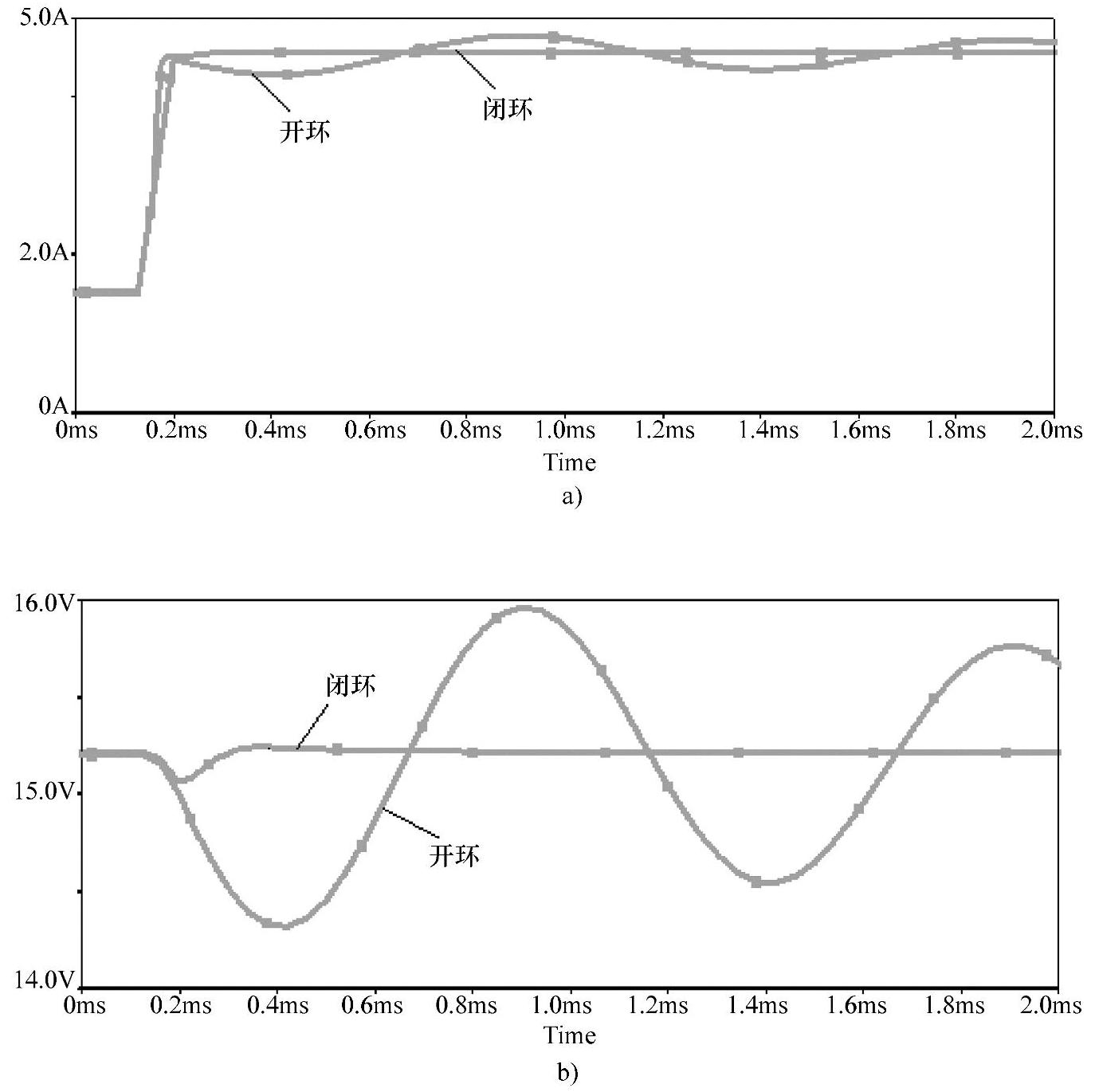
图4-72 突增负载时Buck调节系统瞬态响应特性

a）负载电流瞬态响应 b）输出电压瞬态响应