在本书第2章中已详细介绍了峰值电流控制型开关调节系统，由系统的工作原理可知，当功率开关晶体管的峰值电流等于控制信号（即电压控制器的输出信号）时，功率开关晶体管关断。在峰值电流控制系统中，不是直接控制功率开关晶体管的占空比，换句话说，它的占空比是由控制信号和变换器的电压（或电流）共同决定的。为了便于对峰值电流控制（CPM）系统的仿真，这里介绍在OrCAD/PSpice中建立CPM控制器的大信号平均模型。

由于变换器根据实际带载情况，系统可能工作在CCM下或工作在DCM下，这里讨论的CPM仿真模型，同时考虑了这两种工作模式，为了便于分析，如图4-23所示给出了两种工作模式下的峰值电流控制的主要波形。结合本书2.3.2节中峰值电流控制型开关调节系统中介绍的内容，图4-23所示的i_c为CPM控制器的控制信号，其上附加了斜率为-m_a的人工补偿斜坡，i_L（t）和u_L（t）分别为电感电流和电压，i_pk为峰值电流，＜u₁（t）＞_Ts和＜u₂（t）＞_Ts分别为（0，dT_s）区间和（dT_s，T_s）区间内的电感电压平均值。

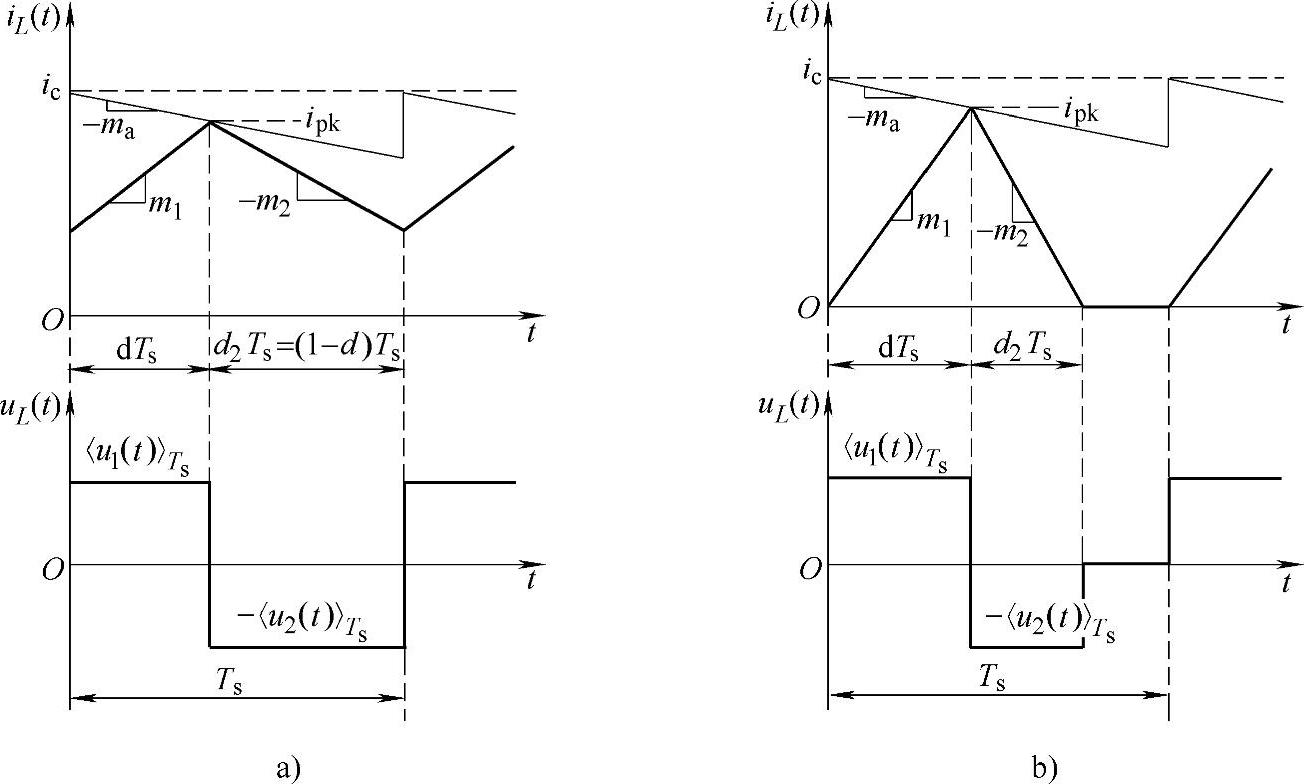
图4-23 峰值电流控制的主要波形

a）工作在CCM下的波形 b）工作在DCM下的波形

在（0，dT_s）第1个区间内，功率开关晶体管导通，电感电流以斜率m₁上升，则有

假设电压纹波很小可被忽略，加在电感的端电压u₁（t）近似等于平均电压＜u₁（t）＞_Ts。在电感电流i_L（t）等于峰值电流i_pk时，时间经过了t₁=dT_s，功率开关管关断，峰值电流的表达式为

i_pk=i_c-m_adT_s （4-23）

在（dT_s，d₂T_s）第2个区间内，功率开关晶体管关断而续流二极管导通，电感电流以斜率-m₂下降，因假设电压纹波很小可被忽略，加在电感上的端电压u₂（t）可近似等于平均电压＜u₂（t）＞_Ts，则有

第2个区间时间经过了t₂=d₂T_s，在CCM下，第2个区间时间持续到一个开关周期的结束，所以有

d₂=1-d （4-25）

而在DCM下，电感电流在一个开关周期结束前就已下降为零，第2个区间时间为

所以有

若变换器运行在DCM下，由式（4-27）计算得到的d₂是小于（1-d）的；若变换器运行在CCM下，（1-d）小于由式（4-27）计算所得的d₂。因此，在OrCAD/PSpice的模型中是用第2个区间长度判断变换器的工作模式的。

为了找到同时适合CCM和DCM两种工作模式的电感电流表达式，下面通过计算面积的方法推导电感电流平均值的表达式：(www.daowen.com)

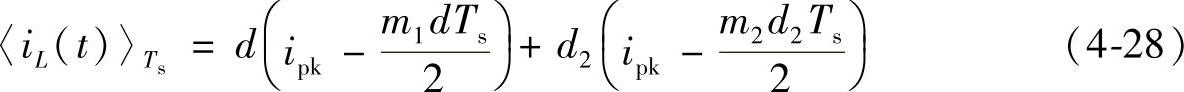
当第2个区间的时间长度是选择式（4-27）和式（4-28）两计算值中的最小值时，则式（4-28）（电感电流平均值的计算式）同时适合CCM和DCM两种工作模式。

根据式（4-22）～式（4-28），平均CPM控制器模型如图4-24所示，该模型由5个信号组成（4个输入信号和1个输出信号）。输入信号中＜u_c（t）＞_Ts=R_f＜i_c（t）＞_Ts为控制信号，R_f＜i_L（t）＞_Ts为电感电流采样信号，＜u₁（t）＞_Ts和＜u₂（t）＞_Ts分别为两个时间区间内电感电压的平均值。输出信号为功率开关晶体管的占空比d。电路参数有采样电阻R_f、开关频率f_s、电感L和人工斜坡补偿幅度V_a。其中人工斜坡补偿幅度为

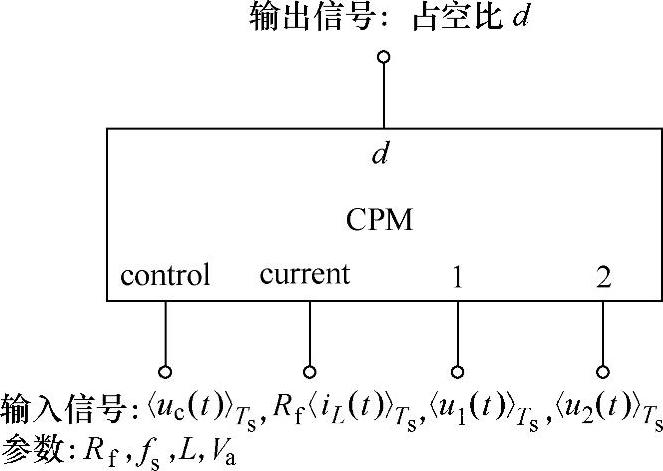
图4-24 CPM子电路图

V_a=m_a^Ts （4-29）

在实现CPM模式子电路时，第2个区间时间长度是选择式（4-25）和式（4-26）得到的两计算值中的最小值，即有

将式（4-23）代入式（4-28），可得到如下占空比表达式：

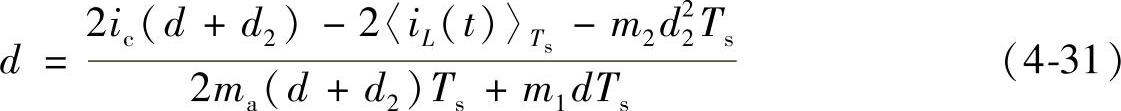
在式（4-31）中，由于等式两边都含有占空比d，因此在计算机仿真过程中是通过叠代方式求解d的。

由式（4-23）、式（4-28）、式（4-30）和式（4-31）可得到CPM的Or-CAD/PSpice模型，其子电路网表联接如图4-25所示，它是以器件名为CPM存放在用户库中，可方便调用。

图4-25 峰值电流控制的大信号OrCAD/PSpice模型子电路网表联接

需说明的是，该OrCAD/PSpice子电路的名称为CPM，电路的参数：电感L、开关频率f_s、斜坡补偿电平V_a和等效电流的采样电阻R_f。这些参数在子电路的默认值分别为：L=100μH，V_a=0.5V，f_s=100kHz，R_f=0.1Ω。

如图4-26所示给出了峰值电流控制的大信号模型在实际控制Buck变换器时的仿真电路，相关的具体应用将在本章4.4节中详细介绍。

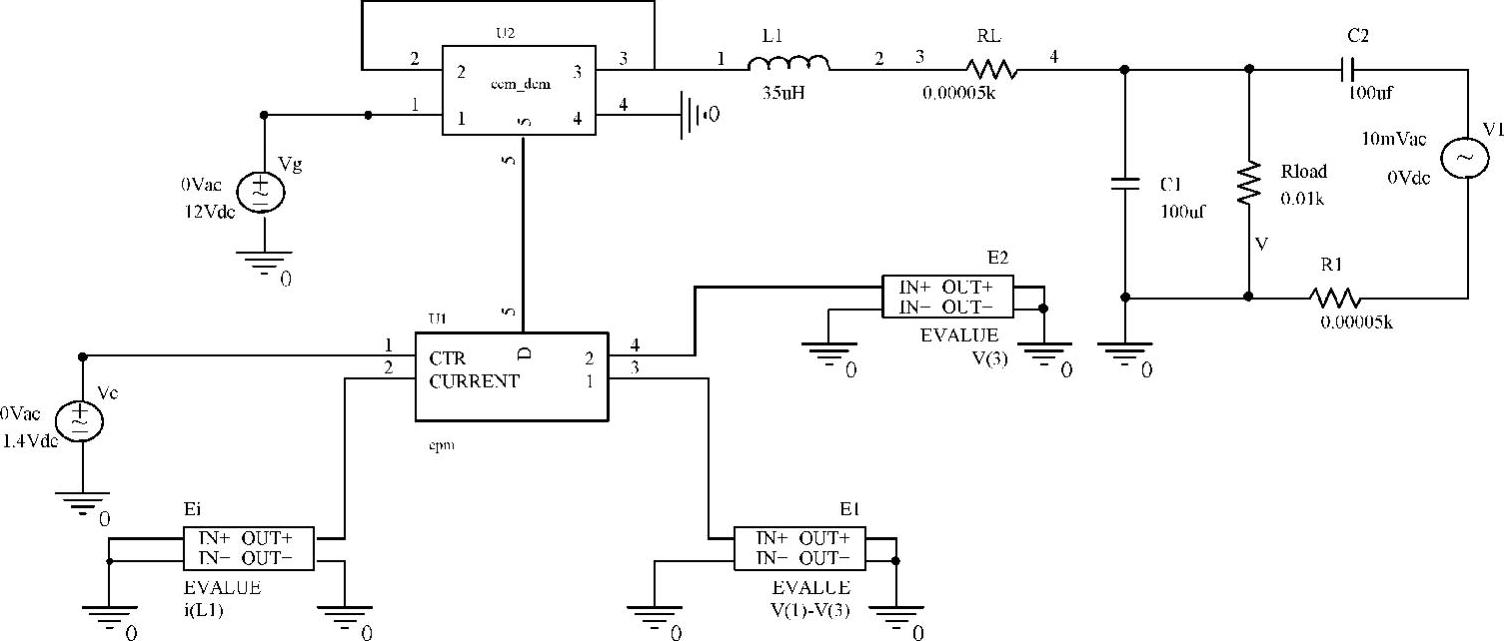
图4-26 CPM控制Buck变换器仿真实例