所谓电荷控制就是在一个开关周期内对流过功率开关管电流的检测信号积分，得到表征输入总电荷量的电压信号，通过控制这个电压去控制输入的总电荷量，亦即控制输入的平均电流[20]。电荷控制属于电流型单周期控制，是一种新型的非线性控制技术。

1.基本工作原理

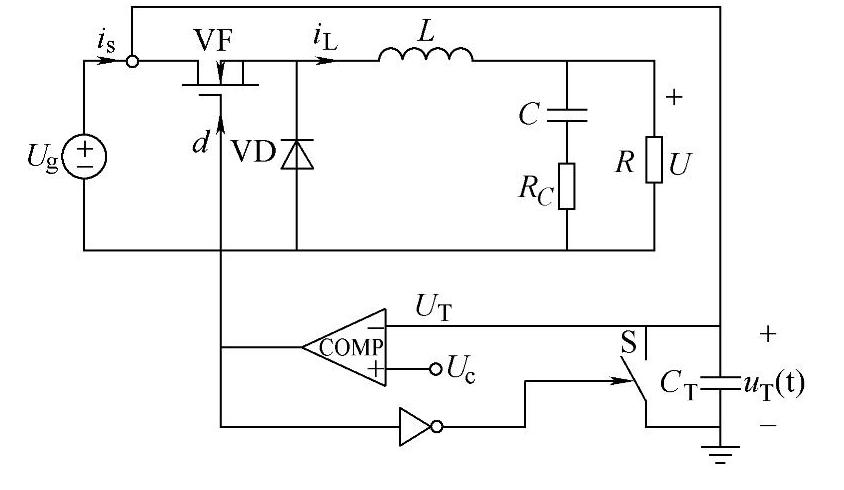
图2-84 电荷控制的Buck变换器原理图

图2-84所示为应用于Buck变换器的电荷控制基本原理图。

功率开关管VF在每个开关周期开始时闭合，开关电流对电容C_T充电，当电容C_T上的端电压U_T等于控制电压U_c时，功率开关管VF关断，同时S闭合，使电容C_T放电，直到下一个周期开始，C_T再次充电。电压U_T体现了每个开关周期内流过功率开关管电流i_s的总电荷量。这样就能在一个开关周期内控制流过功率开关管的电荷量，从而达到控制输出电压的目的。

如图2-85所示为CCM下的各关键量波形。

2.CCM下电荷控制的小信号模型

根据电荷控制的基本思想，可得到电荷控制的基本控制方程为

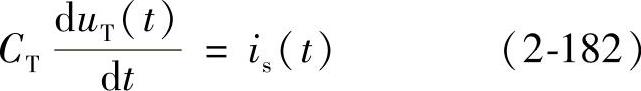
式中，i_s为流过功率开关管的电流，u_T（t）为电容C_T两端的电压。

上式也可表示为

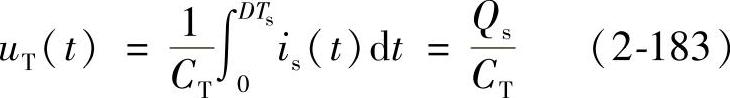
式中，Q_s为功率开关管在DT_s导通时间内输入的电荷量。

考虑到功率开关管导通期间有i_s（t）=i_L（t），则电容C_T上的电荷量为

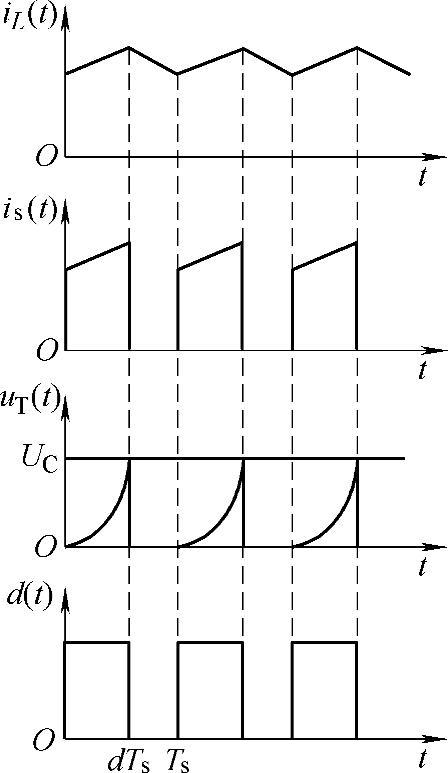
图2-85 CCM下电荷控制各关键量波形

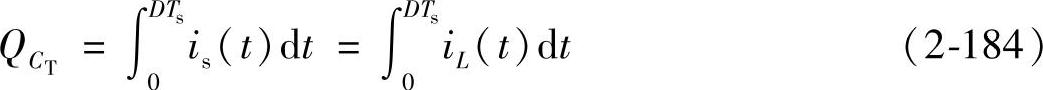
（1）控制电路的离散时间模型

在电荷控制中，开关电流等于功率开关管导通时间内的电感电流，它被积分并与控制电压U_c比较，控制电压来自电压反馈环，即电压控制器的输出电压^[34]。

假设在t=t_k+DT_s时刻，电感电流i_L（t）中引入扰动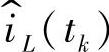，则这个扰动会影响到下一个开关周期，引起开关管导通时间的扰动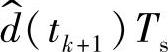，引入电感电流扰动后对开关时间的影响如图2-86所示，图中虚线表示电感电流引入扰动但输入电压、输出电压、控制电压的扰动为零的情况。

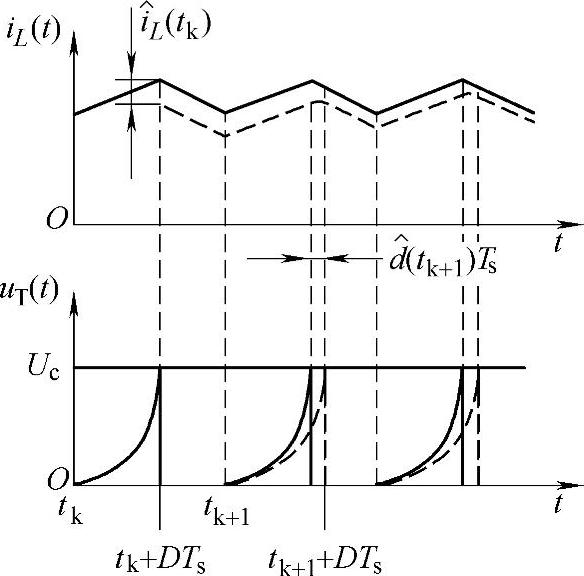
图2-86 电感电流扰动对开关时间影响的曲线

根据式（2-184）和如图2-86所示的情况可得到如下表达式

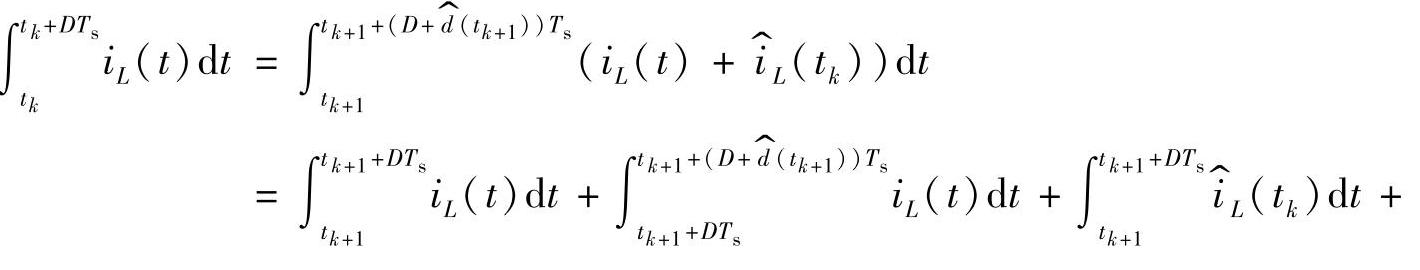
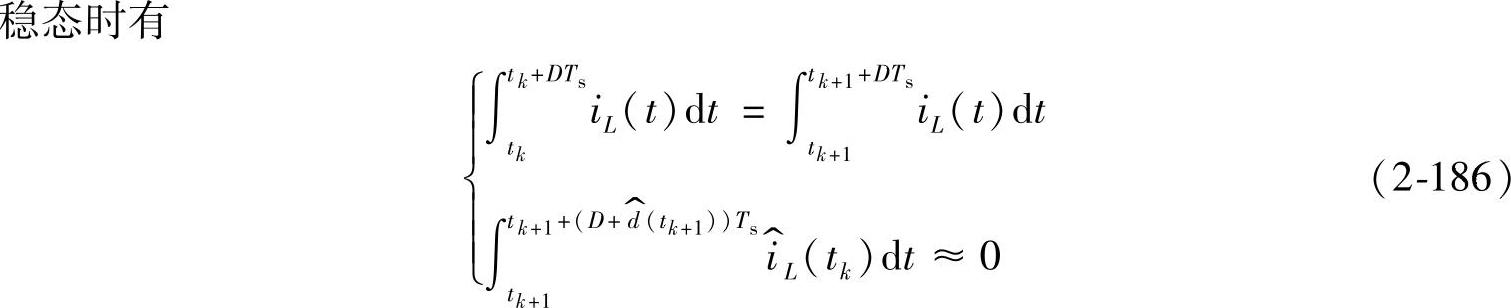
由于引入的扰动满足小信号假设，即

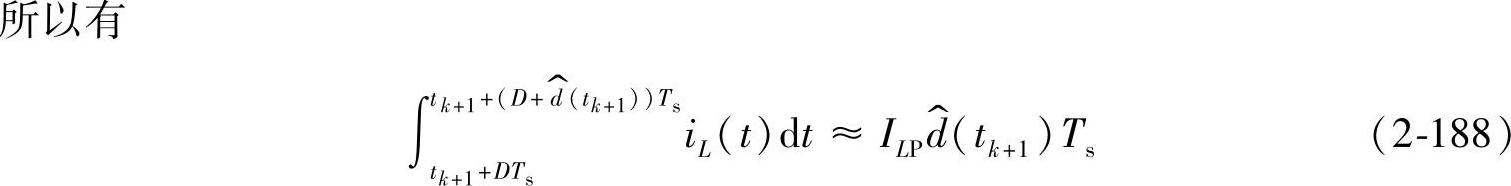
式中，I_LP为电感电流在t=t_k+1+DT_s时刻的值。又因交流小信号的频率f_g远远小于开关频率f_s，即满足低频假设，则在[t_k+1，t_k+1+DT_s]时间内，是常数，因此有

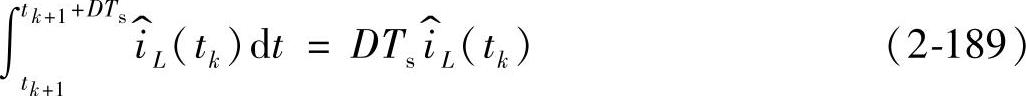
将式（2-186）、式（2-188）、式（2-189）代入式（2-185），可得

上式表明了在t=t_k+DT_s时刻电感电流的变化，引起了t=t_k+1+DT_s时刻占空比的变化。由图2-86可见，在[t_k+1，t_k+1+DT_s]时间内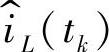，保持不变，又因为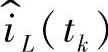和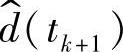之间是离散的，可应用z变换。式（2-190）的z变换为

对应采样连续时间表达式为

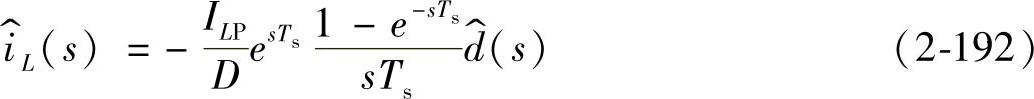
从而可推导得出

（2）电流环的等效

由式（2-192）可知，若电感电流存在扰动，则会在占空比上产生扰动，因此电荷控制电路中存在小信号的等效电感电流反馈环。式（2-193）给出了反馈环的传递函数，电荷控制的等效电流环小信号模型如图2-87所示。

根据图2-87可推导出电感电流-占空比的传递函数为

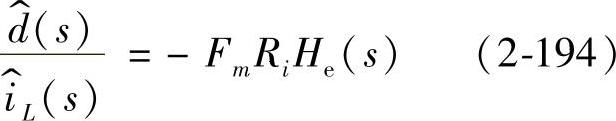
比较式（2-192）和式（2-193）可得

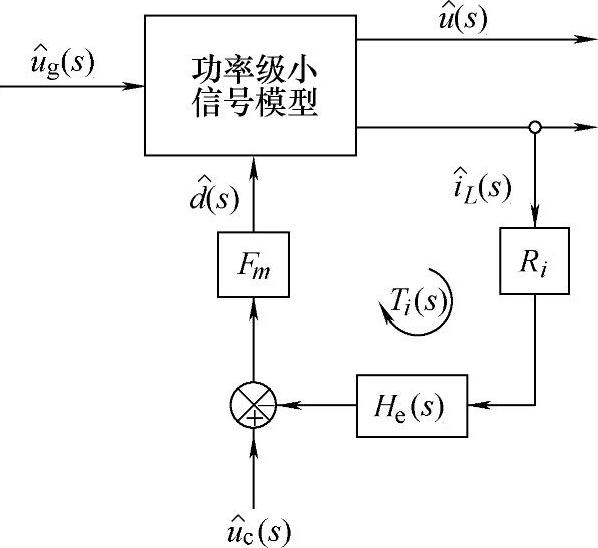
图2-87 电荷控制的等效电流环小信号模型

式中，F_m为调制增益，R_i为等效电流增益（即检测流过功率开关管电流i_s的电阻），H_e（s）为电流环采样传递函数，它与峰值电流控制的采样传递函数具有相同的表达式^[35]。因此，采样传递函数表达式为

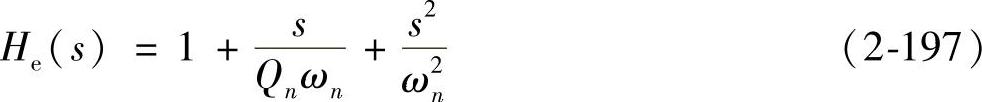
式中，各参数为

ω_n=π/T_s （2-198）

Q_n=-2/π （2-199）

调制增益F_m可从调制器的输入、输出波形推得，图2-88所示为推导调制增益的关键波形。在系统中，若在控制电压中引入一个扰动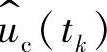，就会在开关管导通时间内产生一个扰动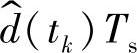，假设输入电压和输出电压扰动为零，即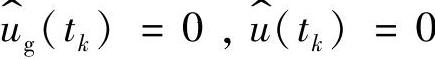，则有

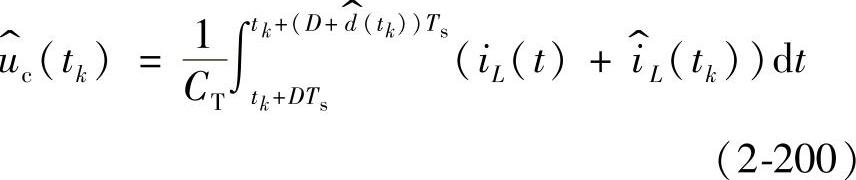
而上式中的电感电流为

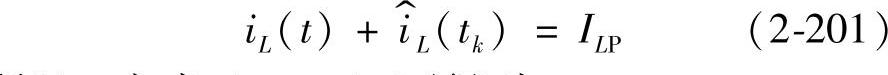
所以，由式（2-200）可得到

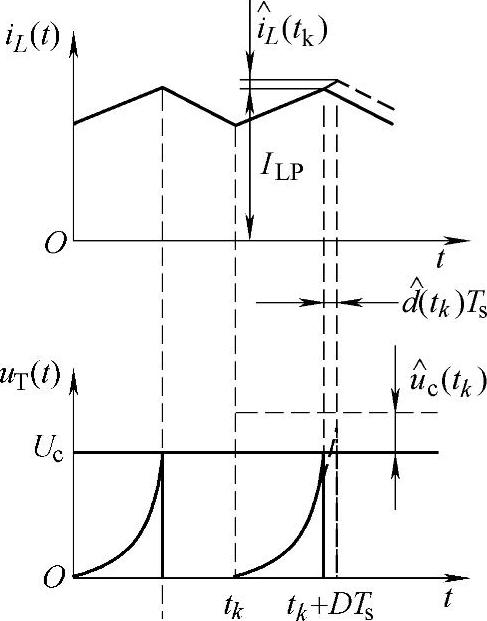
图2-88 推导调制增益的关键波形

比较式（2-194）和式（2-202），得到等效电流增益为

（3）反馈增益和前馈增益

如果在输入电压或输出电压中引入扰动，则在占空比上也会产生扰动，而功率开关管电流的电荷量不仅与占空比有关，同时也是输入电压和输出电压的函数。为此下面分别研究输入电压或输出电压中引入扰动后的情况。如图2-89所示为Buck变换器在输入电压引入扰动后占空比受影响的情况。

由图2-89可见，假设在t=t₀时刻引入输入电压扰动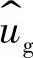，电感电流的上升斜率马上发生变化，使电容充电时间比原先少了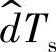的时间，而电容端电压u_T（t）就可达到控制电压U_c值，这表明，输入电压增加将直接导致占空比的减少。

为了描述当出现输入电压扰动或输出电压扰动后，对占空比产生的影响，这里引入了输入电压前馈增益k_f和输出电压反馈增益k_r两个未知参数。

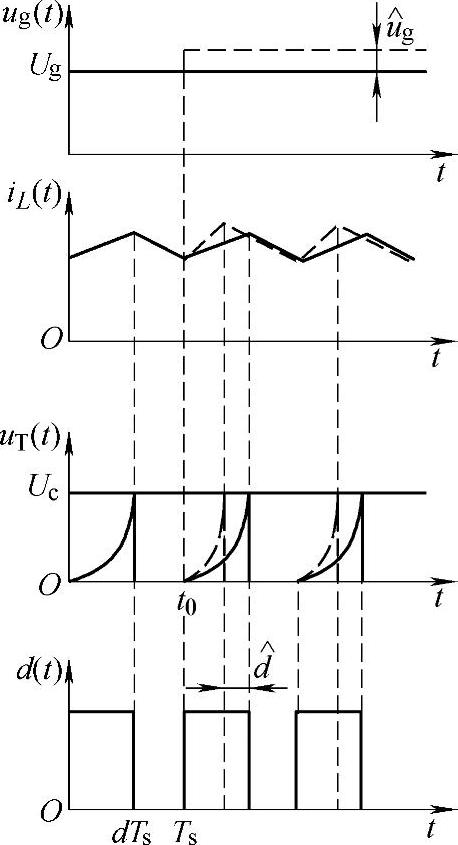
图2-89 输入电压扰动后电感电流和占空比波形

完整的电荷控制小信号模型如图2-90所示，它也是所有PWM变换器电荷控制统一的小信号模型。基本变换器的前馈增益k_f和反馈增益k_r见表2-15^[35]。

表2-15 电荷控制的前馈增益和反馈增益表(www.daowen.com)

（4）等效功率级传递函数

下面以Buck变换器为例分析电荷控制的等效功率级传递函数。

假设Buck变换器的输入电压U_g和输出电压U无脉动，即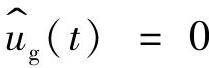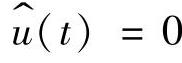，，则可得到如下方程

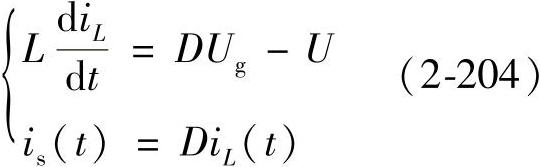
在上式中电感电流和占空比中引入交流小信号扰动，并对其进行拉普拉斯变换后得到

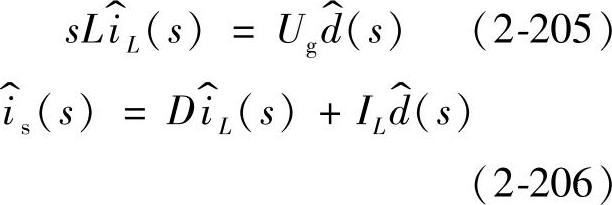
由式(2-205)可得到从占空比一电感电流的传递函数为

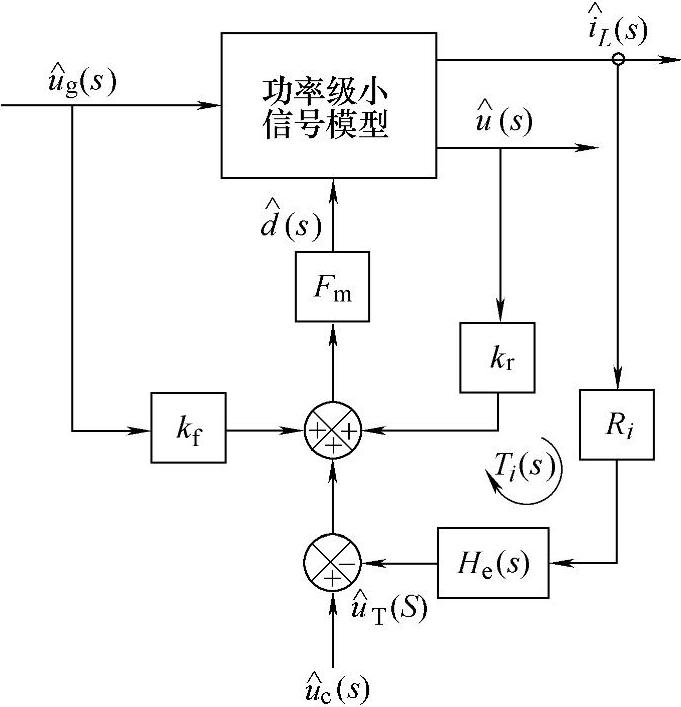
图2-90 完整的电荷控制小信号模型

根据式（2-194）和式(2-207)可画出如图2-91所示的电荷控制型Buck变换器小信号模型。

根据如图2-91所示的电荷控制型Buck变换器小信号模型可得到相应的框图如图2-92所示。这样电荷控制的电流环环路增益为

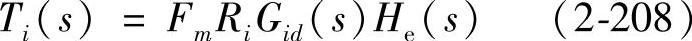
式中，F_m为调制增益；R_i为电流增益；H_e(s)为采样传递函数；G_id(s)为功率级从占空比到电感电流的传递函数，G_id(s)可以像分析平均电流控制的Buck变换器时一样，得到从占空比到电流的传递函数，根据式(2-51)有

所以，电流环环路增益为

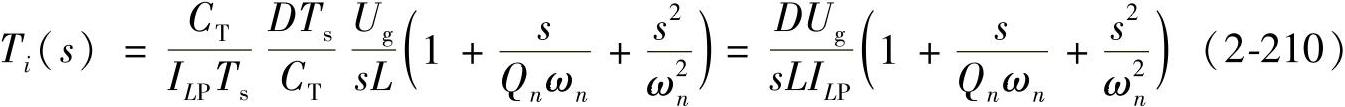
上式也可改写成

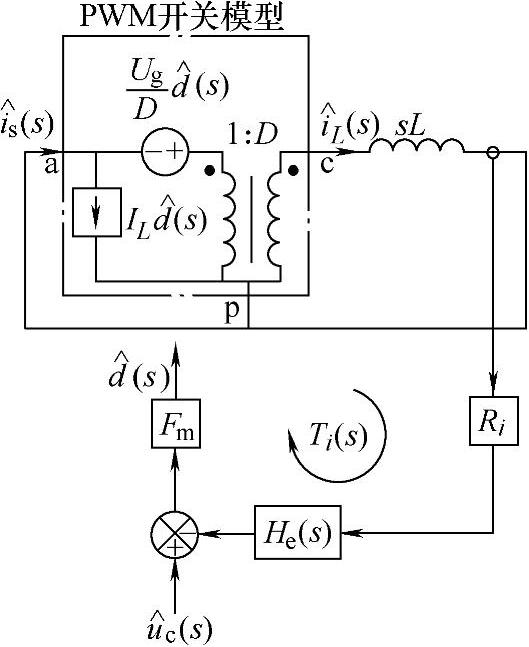
图2-91 电荷控制型Buck变换器小信号模型

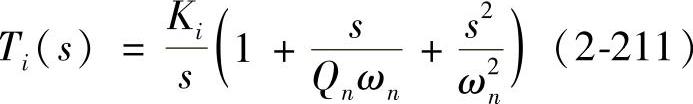
式中，K_i=DU_g/（LI_LP）。

从式（2-211）中可见，电流环环路增益由两部分组成：一部分是积分，另一部分是左半平面的一对共轭零点，两个零点的中心是开关频率的一半。

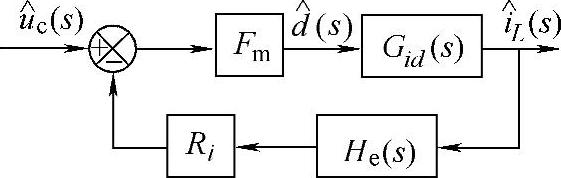
图2-92 电荷控制型Buck变换器框图

根据图2-92电荷控制型Buck变换器框图，可得控制电压-电感电流的传递函数为

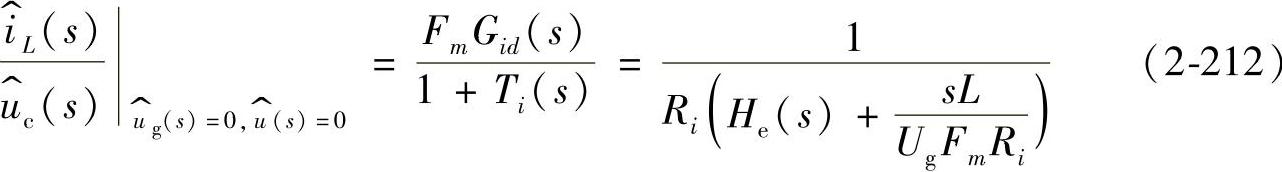
对上式化简可得

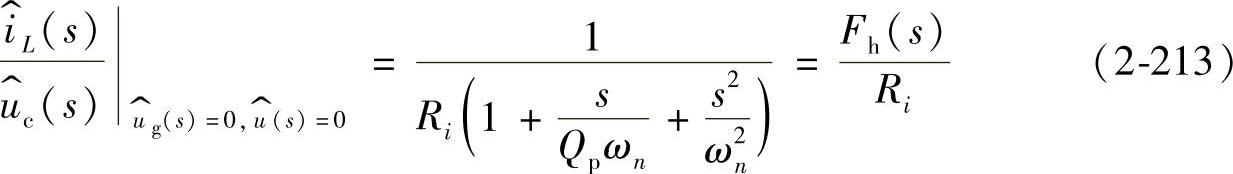
式中，ω_n=π/T_s由式（2-198）给出，Q_p、F_h（s）分别由下式给出

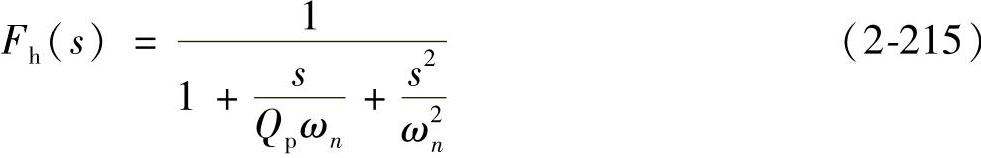
式中，R_eq为等效负载，表2-16列出了基本变换器对应的表达式。

Q_p是F_h（s）双重极点的品质因数。由于电流环的不稳定（又称次谐波振荡）也会影响电压环，因此，讨论电流环的稳定性是很有意义的，而品质因数Q_p能预测电流环的稳定性。

表2-16 基本变换器R_eq的表达式

由式（2-214）可推出，当满足

系统会出现次谐波振荡。电荷控制型变换器存在次谐波振荡是与电源电压和负载有关的^[34]。

系统的稳定条件是Q_p＞0，即D＜2Lf_s/R。可见，系统的稳定性不仅与占空比D有关，还与电路参数L、负载R以及变换器开关频率f_s有关。而前面介绍过的峰值电流控制，电流环的稳定性只与占空比有关。当占空比D＞0.5时，会出现次谐波振荡，需要增设人工斜坡补偿。对于电荷控制而言，通过合理设计，满足

D＜2Lf_s/R （2-217）

系统可在占空比D的全范围内稳定。

对于Buck变换器控制-输出的传递函数（即等效功率级传递函数）近似表达式可由下式给出^[35]

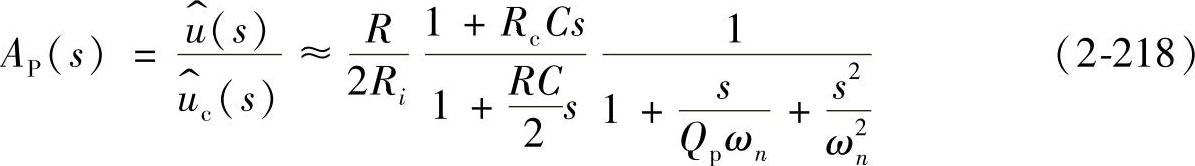
例如：Buck变换器参数：U_g=23V，U=12V，D=0.5，f_s=52kHz，L=67μH，C=370μF，R_C=55mΩ，C_T=2μF。电荷控制型Buck变换器等效功率级传递函数的幅频特性如图2-93所示。为了便于分析，令R_n为变换器的标准负载电阻，则有

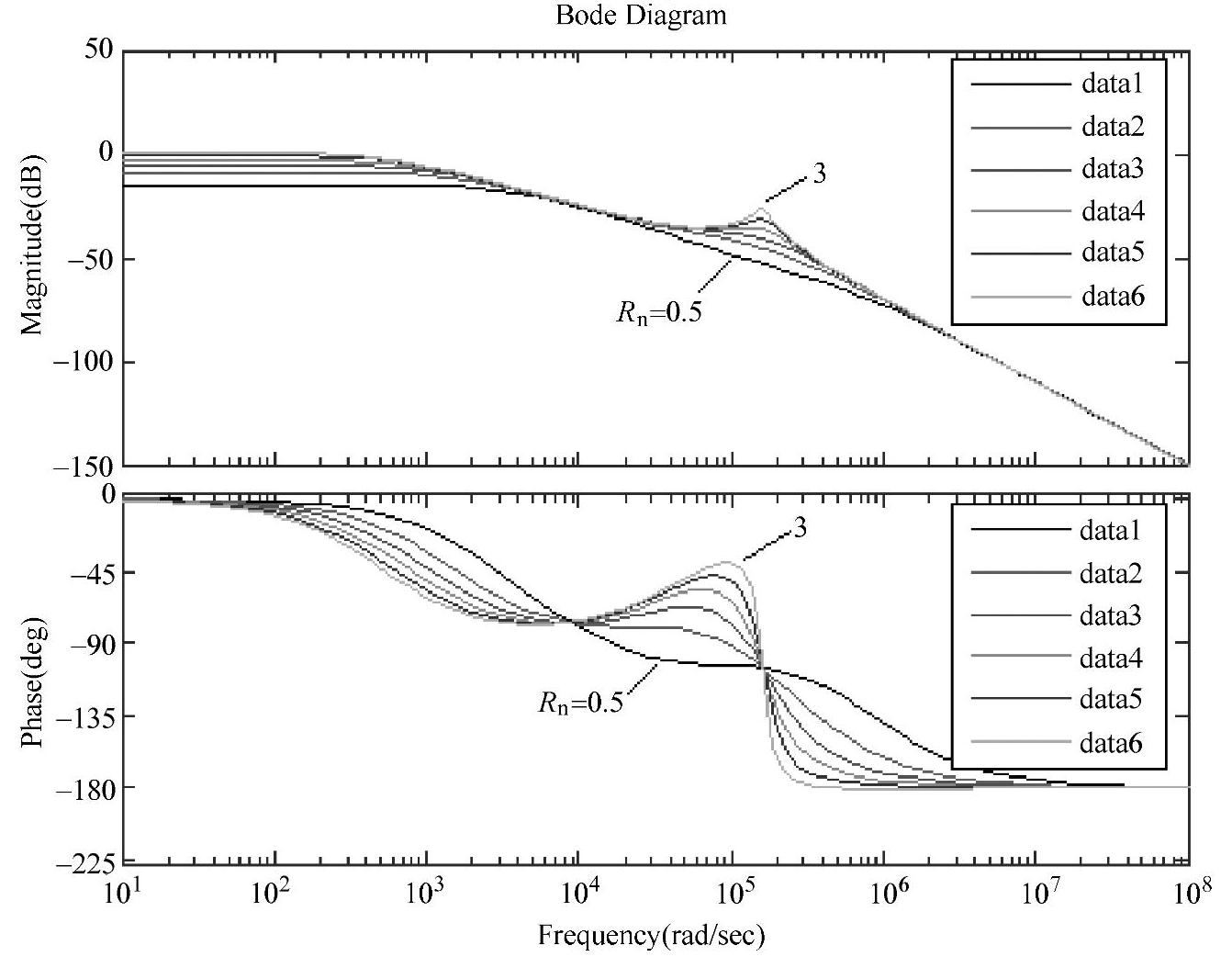
图2-93 电荷控制型Buck变换器

如图2-93中有6条特性，其中标准负载电阻R_n分别为0.5Ω、1.0Ω、1.5Ω、2.0Ω、2.5Ω、3.0Ω。由图2-93等效功率级传递函数的幅相频率特性可见，特性在低频处有一个单极点，在开关频率一半处有一对共轭极点。

（5）参数设计

基于上面对电荷控制型变换器的小信号分析，下面研究在给定的输入和负载的范围内，都能稳定运行的系统参数设计问题。

由式（2-217）可见，次谐波振荡出现在开关频率的一半处（ω_n=ω_s/2），为了防止次谐波振荡，就应在谐振尖峰处增加阻尼，即使品质因数减小，但又不能过阻尼，否则会影响系统的快速性。为此，需要有合适值的品质因数Q_p，考虑最坏情况，即电源电压最高，负载为轻载时，应有

那么变换器的功率级滤波电感应由下式确定

电容端电压u_T（t）的最高值由功率开关管的导通时间和电容器容值C_T两个因数综合决定。为了使系统能正常运行，电容端电压u_T（t）决不能超过比较器的电源电压u_cs，则有

式中，k是小于1的常数，电容器可由下式确定：

在实际应用中，变换器需要运行于空载的情况或在选择功率级参数（如电感L、开关频率f_s）时有一定的灵活性，以及变换器仍然需要具有较宽的电源电压变化范围和较宽的负载变化范围。在这种情况下，为了使系统稳定运行，需要外加斜坡。当电荷控制中引入了外加斜坡，除了调节器的增益F_m发生变化外，图2-90所示的小信号模型仍然适用。外加斜坡后，调节器的增益变为

式中，S_e为外加斜坡的斜率。

等效功率级（即控制-输出的传递函数）的传递函数中的品质因数Q_p也受外加斜坡斜率S_e的影响，变为

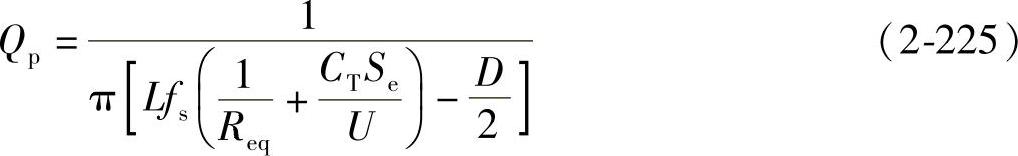
在电荷控制中引入外加斜坡后，设计步骤如下：

第1步：确定电容器，根据式（2-223）确定电容器电容值C_T。

第2步：确定外加斜坡的斜率，在低电源电压和轻载条件下，令Q_p=1，由式（2-225）求出S_e。

第3步：确定等效功率级的传递函数A_P（s），在确定了C_T和S_e之后，根据式（2-218），求出A_P（s）。

第4步：设计控制器，由于在传递函数中只有一个低频极点，可选用具有两个极点、一个零点的补偿网络应用到电荷控制中，从而可获得希望的环路增益。