这里还是以非理想Buck变换器为例分析和研究双环控制型开关调节系统。Buck主电路参数为：输入电压U_g=23.0V，滤波电容C=370μF；电容的等效串联电阻R_C=55mΩ；二极管的开通损耗电阻R_VD=54.7mΩ；MOSFET的开通损耗电阻R_on=82.10mΩ；电感的等效串联电阻R_L=51.2mΩ；CCM下动态电感L=66.64μH，负载R=5.2Ω，输出电压U=11.4V，f_s=52kHz，采用峰值电流控制，利用PWM控制IC中C_T上的电压信号作为斜坡补偿网络的输入信号，实验样机采用UC3825芯片。双环控制型开关调节系统原理示意图如图2-71所示。

首先，在PSpice仿真软件环境下，建立如图2-72所示的组合型CCM-DCM平均开关模型和如图2-73所示的峰值电流控制器的PSpice模型——CPM（有关建立仿真模型的内容将在本书第4章中介绍），再根据实际主电路画出仿真电路，如图2-74所示（在CCM下）。

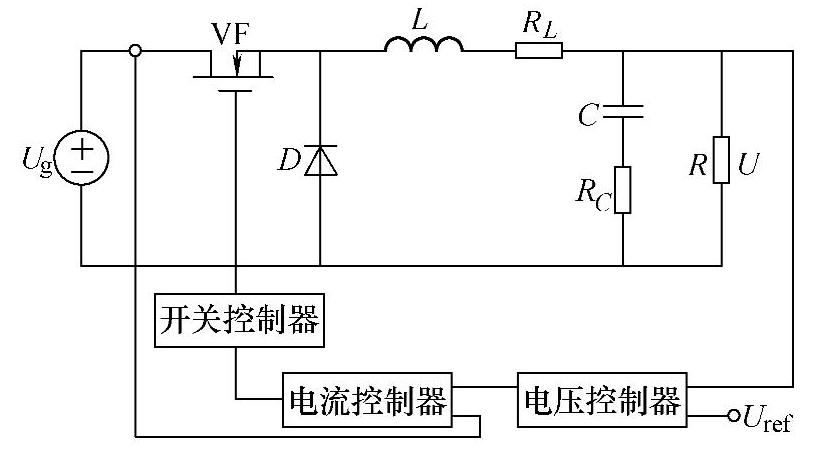
图2-71 双环控制型开关调节系统原理示意图

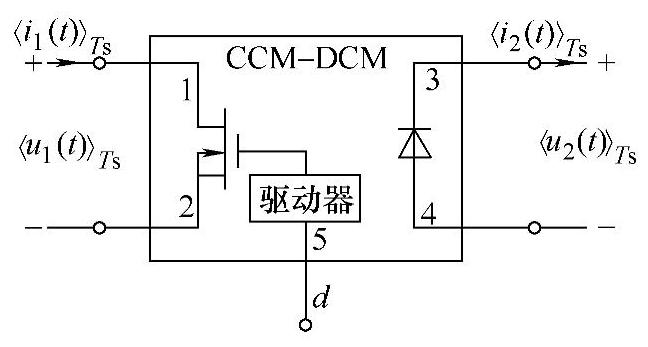
图2-72 组合型CCM-DCM模型

下面分析峰值电流控制对开关变换器功率级动态特性的影响。

1.控制-输出传递函数的频率特性

用图2-74的CPM控制Buck变换器仿真模型，变换器工作在CCM下，在静态工作点的基础上进行两次AC扫描仿真。

为了便于叙述，定义占空比-输出电压的传递函数G_ud（s）为原功率级的传递函数，其输入量与输出量分别为功率开关管VF占空比和变换器的输出，原功率级的传递函数表征了采用直接占空比控制模式时，变换器主电路的动态特性。定义控制-输出的传递函数G_uc（s）为新功率级的传递函数。新功率级包括了变换器主电路和峰值电流控制器，其输入量和输出量分别为峰值电流控制器的输入控制信号（在双环控制时，这个控制量为电压控制器的输出信号）和变换器的输出。新功率级的传递函数表征了采用峰值电流控制模式时，变换器主电路的动态特性。

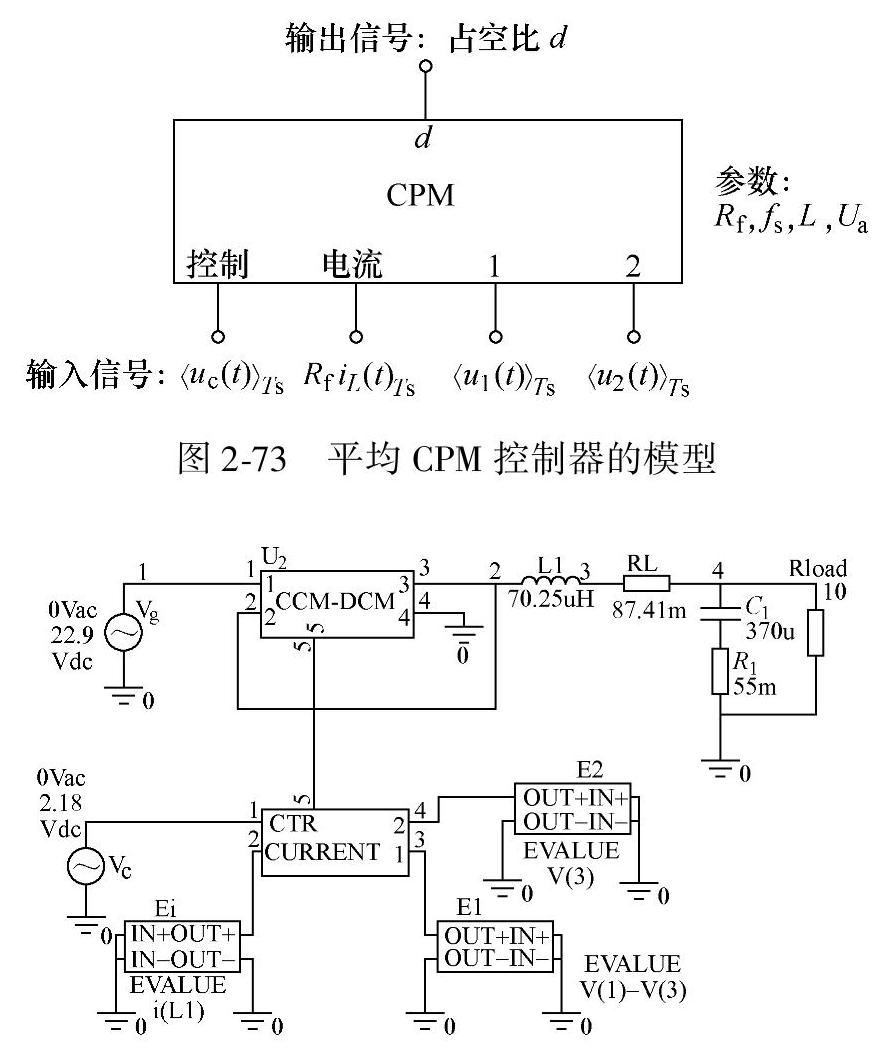
图2-74 CPM控制Buck变换器仿真模型

求取原功率级的传递函数G_ud（s）的方法：在图2-74电路中，去掉CPM控制器，在图2-74中CCM-DCM的5端施加一个带有直流偏置的交流电压源。通过已计算出的开关占空比（D）静态工作点的数值得到直流偏置电压为0.498V，交流电压的幅值为1mV，输出电压的初值U=8.1V，电感电流的初值I_L=0.81A。在上述初值的基础上进行AC扫描。

求取新功率级的传递函数G_uc（s）的方法：在图2-74电路中，在CPM模型的CTR端施加一个带有直流偏置的交流电压源。直流偏置电压U_c=2.18V，交流电压的幅值为0.1mV。开关占空比的初值D=0.498；输出电压的初值U=8.1V；电感电流的初值I_L=0.81A。在上述初值的基础上进行AC扫描。

两次AC扫描得到的仿真曲线如图2-75所示。

从图2-75的仿真曲线可见，原功率级的传递函数G_ud（s）是一个高Q值的二阶系统的响应，它具有双重极点。在双重极点处，幅频特性幅值有一个尖峰，相频特性从0°～-180°的急剧变化。新功率级传递函数G_uc（s）是一个含有两个极点的系统。主极点（低频极点）的频率在0.1～1kHz之间，其数值近似等于负载电阻和滤波电容决定的极点频率；另一个极点约在开关频率的一半处。因此，就设计者关心的频率范围（直流到开关频率的一半），新功率级的传递函数是一个一阶系统。这也证明了CPM控制器的作用是将原二阶系统变为一阶系统。新功率级的另一个特点是在很宽的频率范围内相位滞后都在-90°左右。一个高频极点使得在较高的频率处增加了额外的相位延迟。比较图2-75中的两种频率特性曲线，CPM控制优于占空比控制，又因为新功率级的传递函数在低频处是一个一阶系统，所以容易设计电压反馈环。

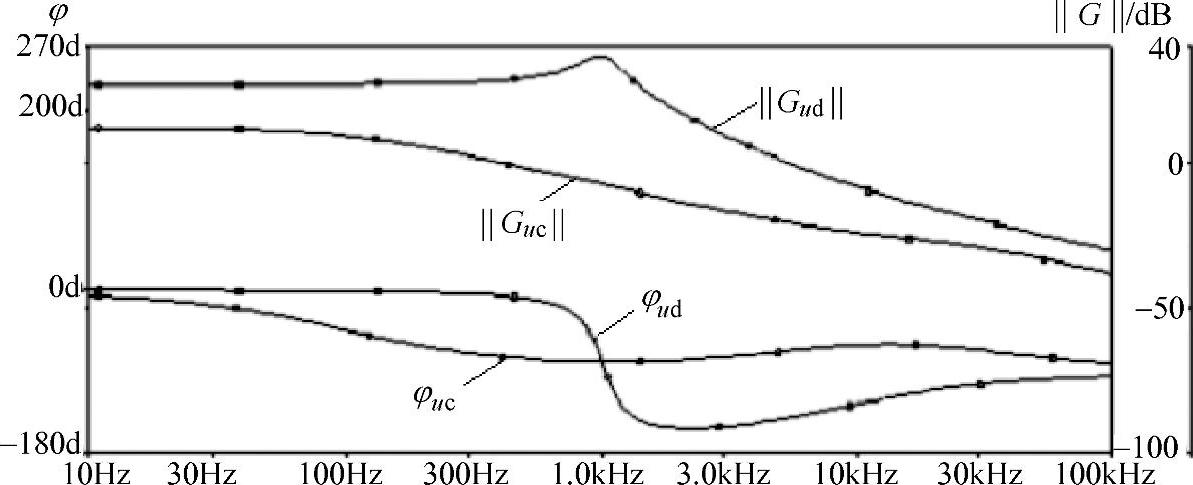
图2-75 Buck变换器CPM控制与占空比控制的控制-输出频率特性曲线比较

2.音频衰减率(www.daowen.com)

峰值电流控制的另一优点是具有很强的抑制电源电压扰动的能力，这同样可通过仿真来验证。在如图2-74所示的电路中，去掉CPM控制器，在CCM-DCM的5端施加一个直流电压源，已计算出的开关占空比（D）静态工作点的数值得到直流偏置电压为0.498V；在CCM-DCM的1端施加一个带有直流偏置的交流电压源。直流偏置为直流输入电压22.9V，电压源的幅度为0.1mV，输出电压的初值U=8.1V，电感电流的初值I_L=0.81A。在上述初值的基础上进行AC扫描，得到原功率级G_ug（s）的频率特性。同理，对新功率级G_uc（s）仿真，可得到G_uc（s）的频率特性，两个仿真结果如图2-76所示。比较两条仿真曲线，在100Hz附近，CPM控制方式对输入电压扰动的衰减要比占空比控制方式至少少了10dB。这说明电流反馈可大大降低输入电压波动对输出电压产生的影响。

3.输出阻抗频率特性

测量输出阻抗的方法是在变换器输出端施加一个交流电压源，测量其电流。

如图2-77所示为原功率级和新功率级仿真电路，相应的仿真结果如图2-78所示。从中可见，在占空比控制的变换器（原功率级）中，低频段的输出阻抗很小，原因是在低频段，因电感感抗很小，输出阻抗又主要取决于电感的阻抗。但随着频率的上升，电感的阻抗增大，输出阻抗也跟着增大，所以在输出LC滤波器的谐振频率处，输出阻抗出现了一个尖峰。随着频率继续更高的上升，输出阻抗主要取决于滤波电容的阻抗，它随着频率的增大而减小。

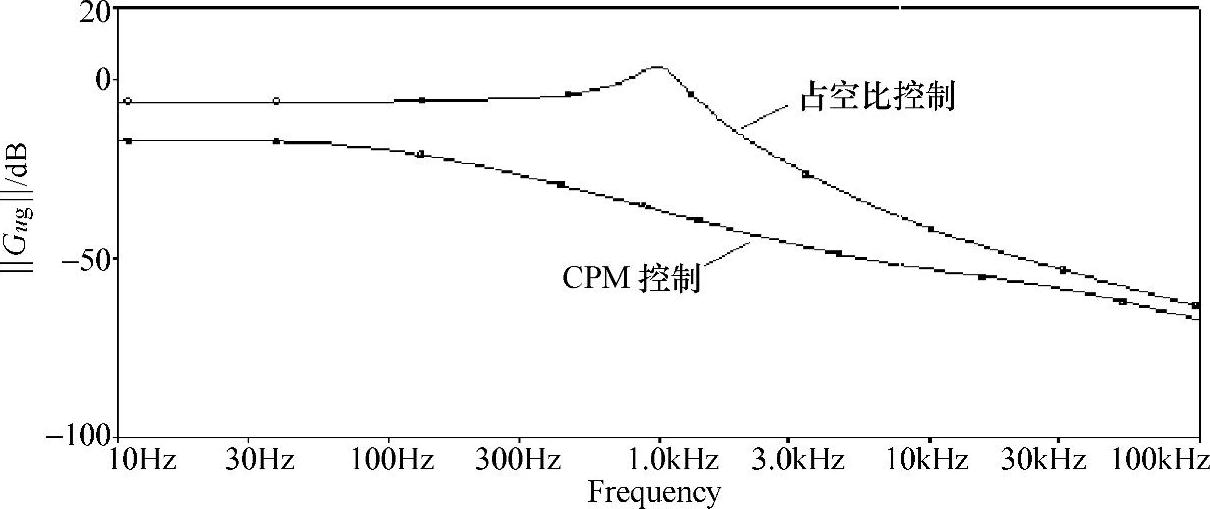
图2-76 Buck变换器CPM控制与占空比控制的输入-输出的频率特性曲线比较

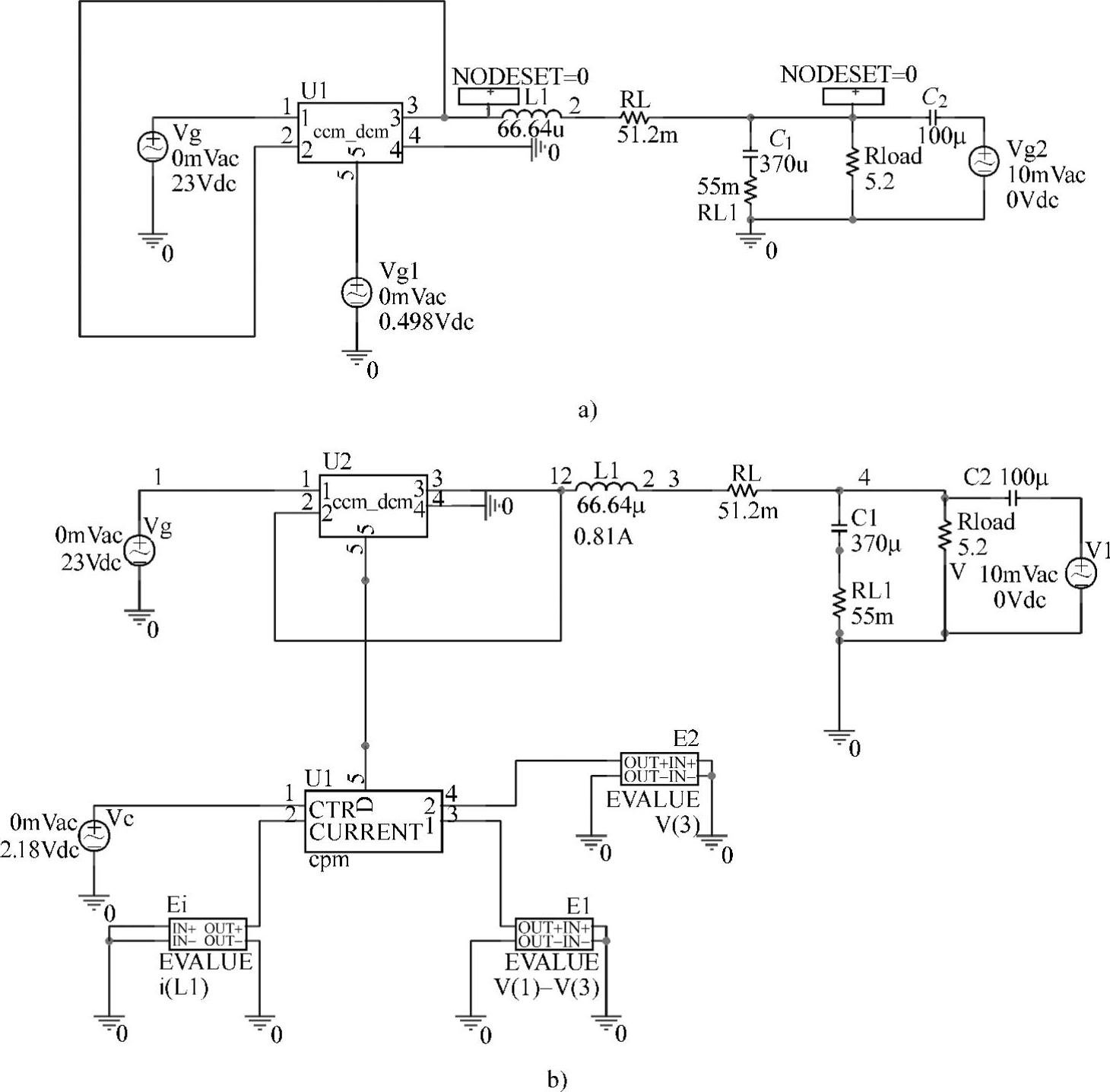
图2-77 Buck变换器输出阻抗频率特性仿真电路

a）原功率级 b）新功率级

对于CPM控制的变换器（新功率级），低频阻抗很高，它等于负载电阻与输出电容的并联。由于CPM控制使得系统变为一个一阶系统，即在低频段，电感不会影响系统的特性，包括输出阻抗。随着频率的上升，输出阻抗主要由滤波电容决定，且随着频率的增加而不断减小。在高频段，占空比控制的变换器与CPM控制的变换器的输出阻抗有着相同的渐近线。

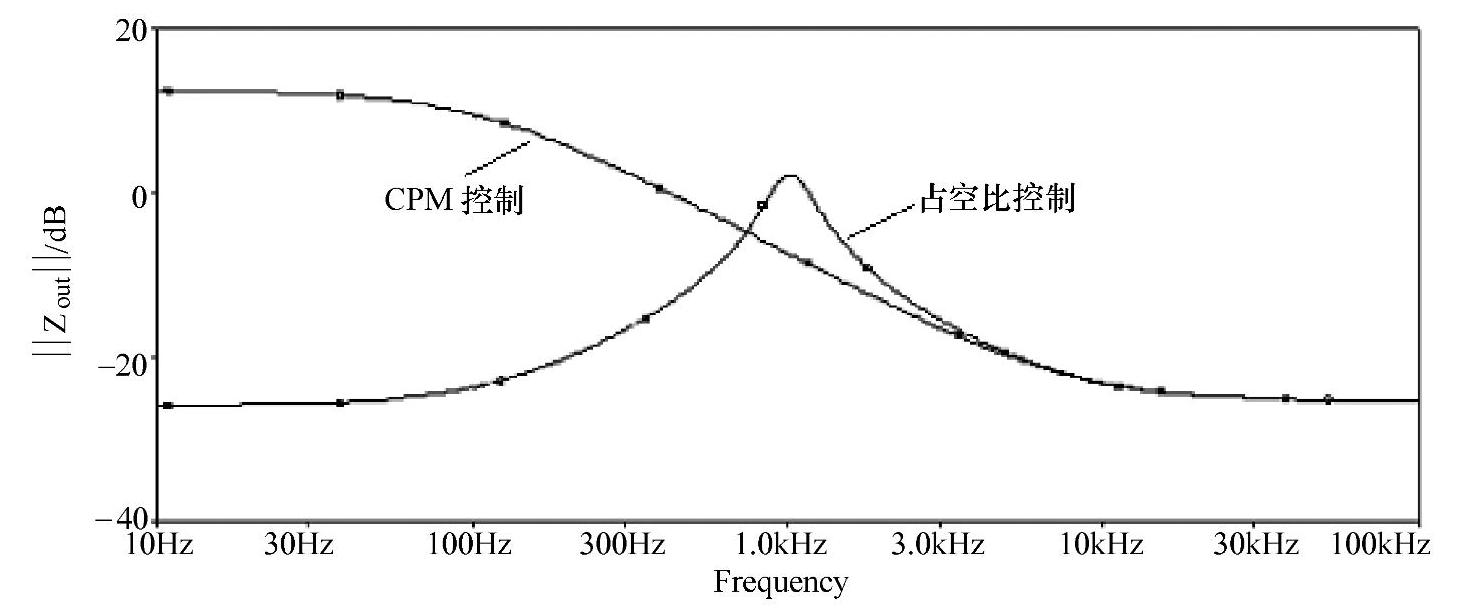
图2-78 Buck变换器输出阻抗频率特性曲线

用Agilent 4395A网络/频谱/阻抗分析仪测试系统的等效功率级传递函数，即测试G_uc（s）（关于实验测试的内容将在本书第5章介绍），测得如图2-79a所示CCM的实测曲线。调节负载使系统工作在DCM下，用同样的方法对开关调节系统进行仿真和实验测试，可得到在DCM下的等效功率级传递函数的仿真和实测曲线如图2-79b所示。实测曲线与仿真曲线相吻合，表明所建的仿真模型的准确。

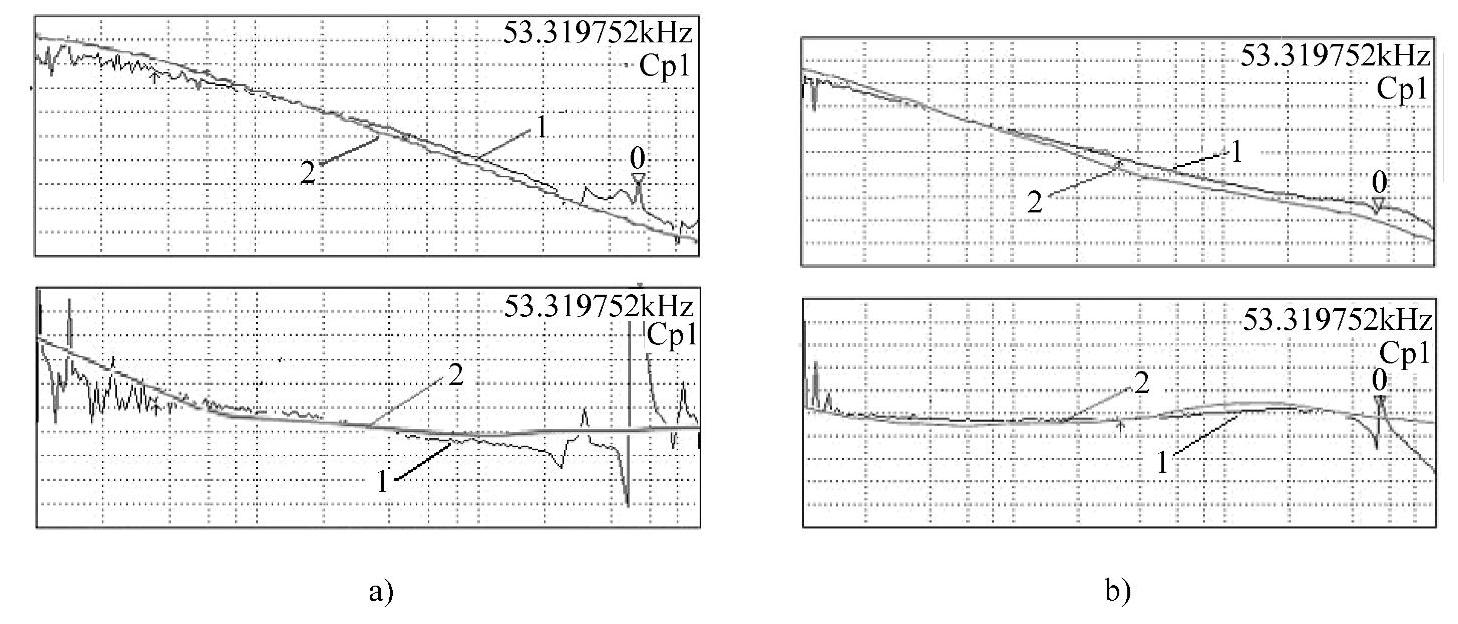
图2-79 CPM控制Buck变换器等效功率级传递函数仿真和实测曲线

a）开关调节系统在CCM下 b）开关调节系统在DCM下

1—实测曲线 2—仿真曲线