1.平均电流控制型开关调节系统的组成和基本工作原理

如图2-27所示为基于Buck变换器的平均电流控制型开关调节系统，电流控制环是由部分开关变换器、电流采样网络、电流控制器和开关控制器（PWM比较器、时钟电路和触发器）等组成。若将电流控制环和开关变换器等效成新功率级如图2-27a中的点划线框所示，电压控制环则由电压采样网络、电压控制器和等效功率级电路组成。图中电流环的平均电流是选取电感电流作为反馈信号，但由于电感电流中含有较大的交流分量，所以一般采用霍尔电流传感器或直接串联电阻的方法采集电流，而不采用电流互感器。其中霍尔电流传感器适用于大电流和需要隔离的场合。但常用的霍尔电流传感器的响应速度较慢，适用于开关频率在100kHz以下的工作场合。如图2-27所示的电流采样是用直接串联电阻的方法，如图中的电阻R_s，这种电流采样方法的特点是简单、可靠、不失真且响应速度快，但是损耗大、不隔离，适用于小电流并无需隔离的电路。

由图2-27a可见，整个系统的控制电路由电压控制器、电流控制器、PWM比较器、时钟电路和触发器、电流采样网络等组成。

平均电流控制型开关调节系统的工作原理是：通过采样电阻R_s将电感电流变为电压反馈信号u_Rs，电压控制器的输出信号u_CP与反馈信号u_Rs的直流成分相比较，决定了电流补偿网络输出电压u_CA的直流成分，即静态工作点。反馈信号u_Rs的交流成分经电流控制器放大后与PWM比较器的另一个输入信号——锯齿波u_R相比较产生占空比的增量。PWM比较器的两个输入信号如图2-27b所示，电感电流的交流成分与电流补偿网络输出电压的交流成分是反相的。当开关管关断时，电感的电流是下降的，而电流补偿网络的输出电压是增加的。而当开关管导通时，电感电流是上升的，电流补偿网络输出电压是下降的。当U_CA=U_R时，开关管关断。

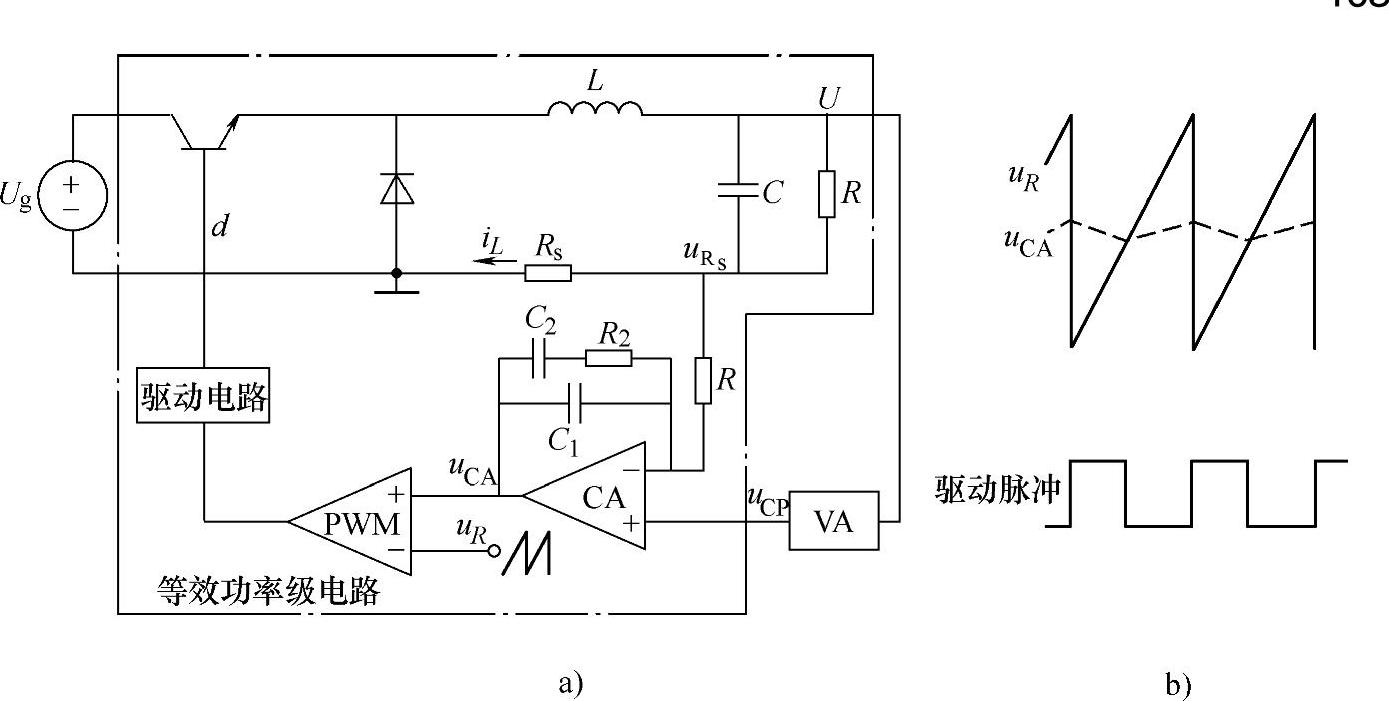
图2-27 Buck变换器的平均电流控制型开关调节系统

a）系统图 b）PWM输入特性比较

参考文献[1]详细介绍了平均电流控制在电流补偿网络的增益提高时可能出现的阻塞现象或次谐波瞬态不稳定现象。为了避免这些问题，平均电流控制系统必须满足斜坡匹配标准，而斜坡匹配问题是一个大信号问题，因此在设计电流环时，应采用大信号设计。

2.电流控制器的大信号设计

为了使电流控制在电流补偿网络的增益时也能可靠地工作，要求PWM比较器两个输入信号的斜率必须满足：对于单极点系统，被放大的电感电流的下降斜率不能超过锯齿波的上升斜率（见图2-27b）。这个标准直接给出了电流补偿网络在开关频率处增益的上限值，也间接地给出了开环传递函数的穿越频率f_c，可以用上述标准求得电流补偿网络在开关频率处的最大增益G_max（f_s）。

为了便于推导控制对象的传递函数，即由电流补偿网络的输出到电流采样电阻R_s两端电压的小信号传递函数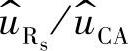，对于CCM型DC-DC变换器，作如下假设：①输出电压的扰动量^u=0，则电压控制器输出电压的扰动量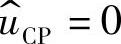；②R_s很小，|ωL|＞＞R_s，ωL+R_s≈ωL；③电流控制器的幅频特性从穿越频率到开关频率保持为一个常数，且|G|=|G_max|。在假设条件下，由本书第1章图1-22给出的统一小信号模型和平均电流控制环可以得到如图2-28所示的等效电路，图中L为等效电感，L、e（s）和M（D）参数的计算公式可在本书第1章的表1-1中查到。

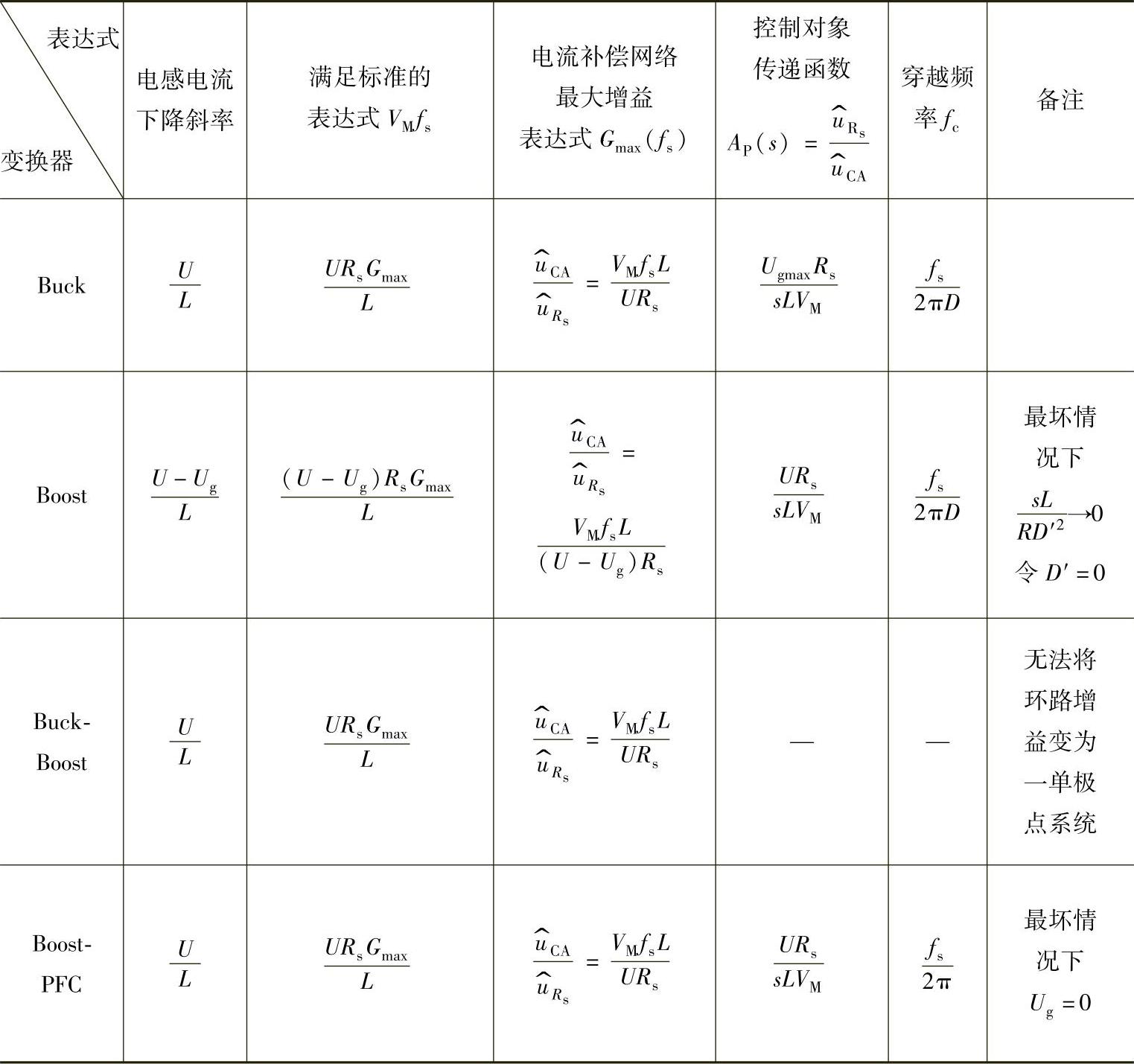
已知锯齿波的上升斜率为V_M/T_s=V_Mf_s和斜率匹配，可得到不同变换器的电流补偿网络的最大增益表达式见表2-5。表2-5各式中U_g、U分别是Buck、Boost、Buck-Boost等DC-DC变换器的直流输入电压和输出电压；L是滤波电感；V_M是锯齿波的峰峰值，表中诸式表示从采样电阻上的电压到电流补偿网络输出电压的增益，即电流控制器的增益。有关表2-5中的表达式，参考文献[1]给出了具体的推导过程，有兴趣的读者可查阅。

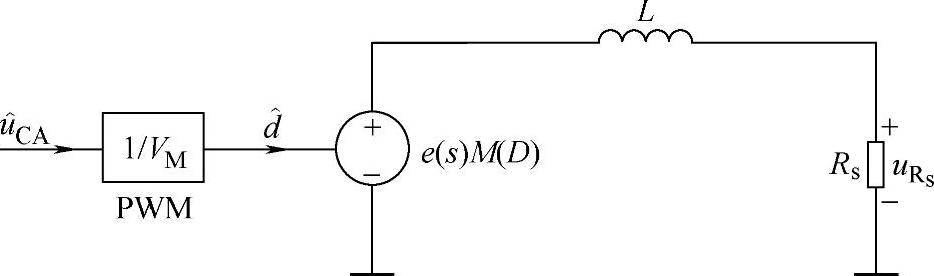
图2-28 求控制对象A_P（s）的等效小信号电路

表2-5 各种变换器电流补偿网络的最大增益一览表

以上讨论了PWM比较器两个输入信号的匹配问题，下面介绍电流控制器的设计。电流控制器的设计方法与前面介绍的电压控制器的设计方法相似。

电流环的控制对象是一积分或近似积分环节^[1]，对于这类控制对象在大信号设计时要求是：①电流补偿网络在f_c～f_s范围内，补偿网络的增益近似恒等于G_max，即幅频特性在中频段较为平坦；②在穿越频率处要有足够的相位裕量。综合考虑上述要求，单极点-单零点补偿网络和具有带宽增益限制的单极点补偿网络作为电流控制器均是合理的。

3.系统的性能分析

以Buck变换器为例，电流控制器选用单极点-单零点补偿网络，分析系统在各频段特性。

由表2-3可知，单极点-单零点补偿网络的传递函数为

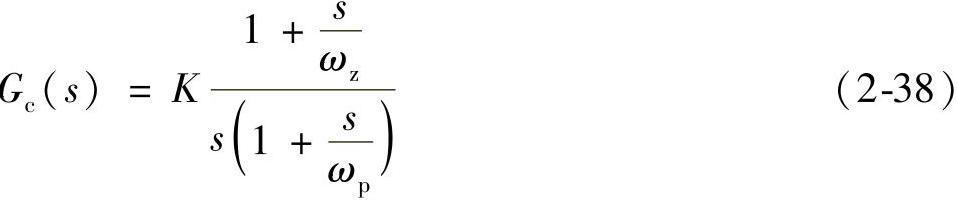
中频段的增益

补偿网络幅频特性的平坦段在f_z～f_p之间，如果令系统的穿越频率和开关频率均位于这个频段内，则这个补偿网络能够满足电流控制环的要求。查表2-5控制对象的传递函数为

所以Buck变换器电流控制环的开环传递函数为

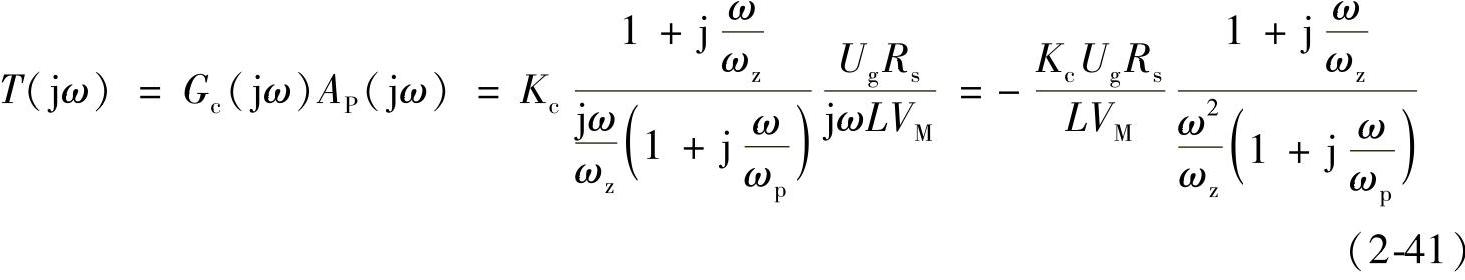
（1）低频段特性

在低频段，0＜f＜f_z，（ω/ω_z）＜＜1，（ω/ω_p）＜＜1，式（2-41）可改写为

由式（2-42）可见，在低频段开环传递函数等效为一个二阶积分环节。在直流频率点附近，系统的增益非常大，故系统的直流输出电流是由其控制信号及电流采样网络决定的，几乎与系统的主电路、电流补偿网络无关。因此，系统对其负载变化的稳态误差等于零。但由于具有一个固定180°滞后相移，系统在低频段是不稳定的。改进的方法是，如果在低频段，系统的开环传递函数等效为一个一阶积分，则可以克服上述缺点。因此，就低频特性而言，针对积分型控制对象，最佳的电流控制器应是具有带宽增益限制的单极点补偿网络。若采用具有带宽增益限制的单极点补偿网络，系统的开环传递函数为

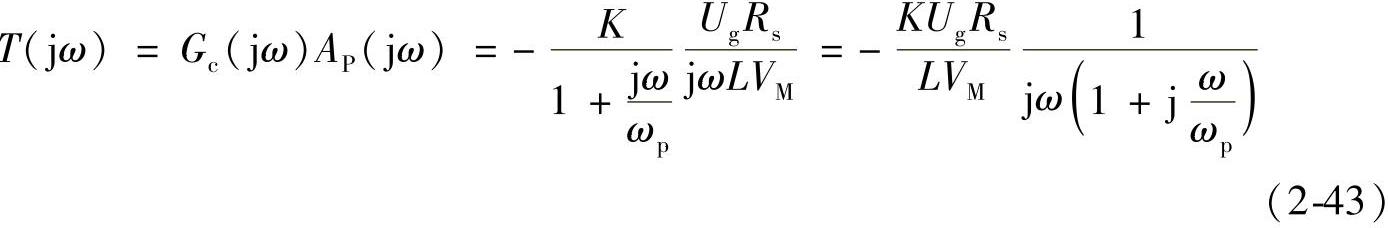
则在低频段，式（2-43）可改写成

由式（2-44）可见，在低频段开环传递函数等效为一积分环节，系统对其负载变化的稳态误差等于零，同时也是稳定的。

（2）中频段特性

在中频段，f_z＜f＜f_p，（ω/ω_z）＞＞1，（ω/ω_p）＜＜1，式（2-41）可改写为

由式（2-45）可见，在中频段幅频特性的下降斜率-20dB/dec，系统等效为一个单极点系统。在中频段相位裕量约为45°，补偿网络在中频段需要一个平坦的幅频特性原因就在此。

（3）高频段特性

在高频段，f＞f_p，（ω/ω_z）＞＞1，（ω/ω_p）＞＞1，式（2-41）可改写为

由式（2-46）可见，在高频段幅频特性的下降斜率为-40dB/dec。因此高频极点的设置是为了抑制高频噪声。一般是将高频极点f_p设置在开关频率处或低于开关频率处：一是为了减少主电路中开关信号高次谐波的影响；二是起抑制由寄生参数而产生衰减振荡信号的作用。

4.平均电流控制型电流环等效模型及闭环传递函数

对于双环控制系统，前面已介绍了内环即电流控制环的设计，若用系统等效分析法将主电路和电流控制环等效成一个新功率级，这样在设计外环即电压控制环时可将整个电流控制环视为控制对象的一个环节，故电流控制环的闭环传递函数的求取是接下来所要研究的问题。

根据如图2-27a所示可得到电流控制环闭环框图，如图2-29所示。

在图2-29中，G_c（s）为电流控制器的传递函数；G_M（s）为PWM调制器的传递函数；G_id（s）为新功率级的传递函数；以CA的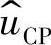作为输入时，CA为一个同相放大器，其传递函数为[1+G_c（s）]。

假设电流控制器采用单极点-单零点补偿网络，则传递函数为

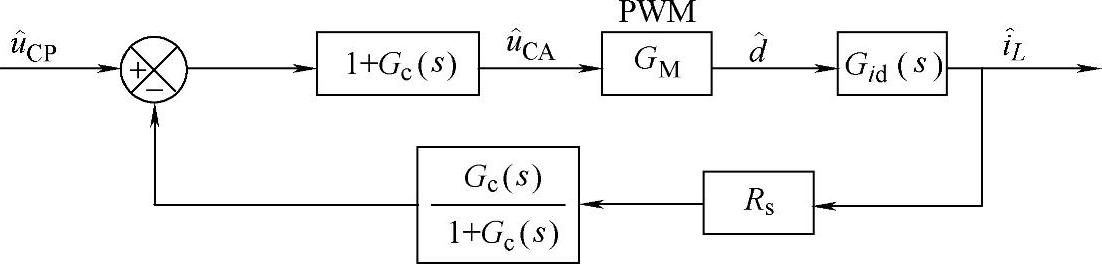
图2-29 电流控制环闭环框图

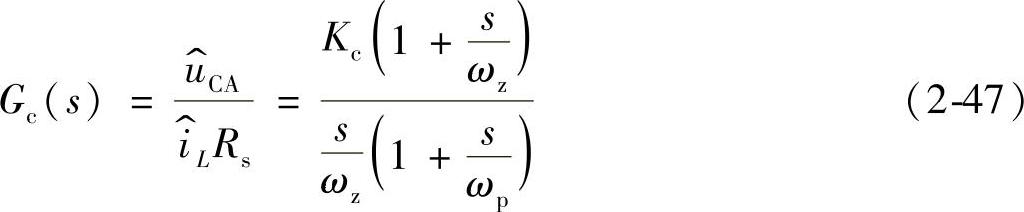(www.daowen.com)

式中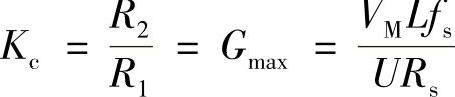，；ω_z、ω_p分别为电流控制器的零、极点角频率。PWM调制器的传递函数为

设电流采样网络的传递函数为H_c。如果电流采样器为电阻R_s，则电流采样网络传递函数为

H_c=R_s（2-49）

功率级的传递函数为

查表2-5和根据式（2-49）、式（2-48）对于Buck变换器功率级的传递函数为

对于Boost变换器功率级的传递函数为

如果采用单极点-单零点补偿网络作为电流控制器，电流环的开环传递函数为

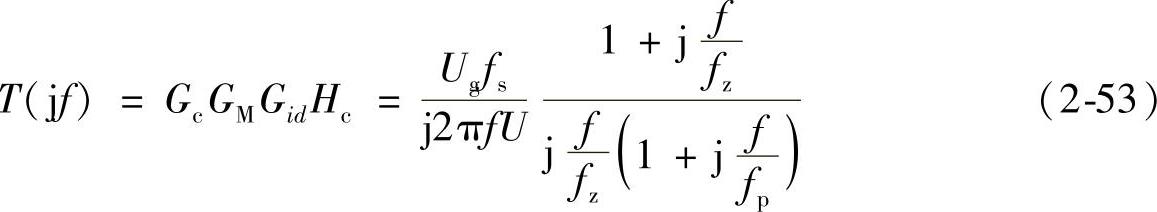
据如图2-28所示，电流控制器输出电压的表达式为

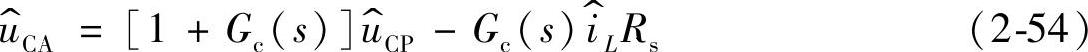
式中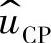，是电压控制器的输出电压即电流控制器的参考电压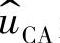；是电流控制器的输出电压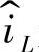；是功率级的输出电流，其值为

将式（2-55）代入式（2-54），得闭环传递函数为

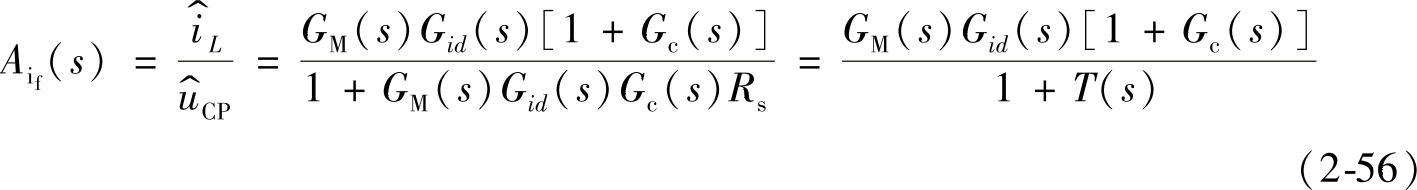
式（2-56）是一个高阶系统，为了简化系统分析和设计，需要对闭环传递函数进行必要的近似处理。

5.闭环传递函数的简化模型^[1]

参考文献[1]指出简化闭环传递函数的方法有两种：一种是分频段的分析开环传递函数，给出其近似表达式；另一种是当电流控制环设计完成后，可以写出其传递函数具体表达式。利用Mathcad或Matlab等数学仿真软件得到这个具体函数的仿真结果，再用一个简单的函数逼近其仿真结果。

模型Ⅰ：在本小节的第3部分“系统的性能分析”中已指出，如果采用单极点-单零点补偿网络作为电流控制器，则在低频段平均电流控制模式Buck变换器的开环传递函数会有较大的幅值。由公式（2-47）可知，在低频段，电流控制器的传递函数也有较大的幅值。假定|T|＞＞10，|G_c（s）|＞＞10，则式（2-56）可简化为如下：

上述模型在f＜＜f_c是有效的。模型Ⅰ表明，在采用平均电流控制模式的变换器中，低频时电感电流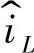具有跟踪控制电压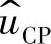的能力，也就是说系统的低频输出电流是由其控制电压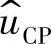和电流采样网络决定的，几乎与系统的主电路、电流补偿网络无关。模型Ⅰ的缺点是忽略闭环传递函数的高频特性。

模型Ⅱ：如果采用单极点-单零点补偿网络作为电流控制器，电流采样网络为电阻R_s，可以用下面双极点模型近似逼近A_if：

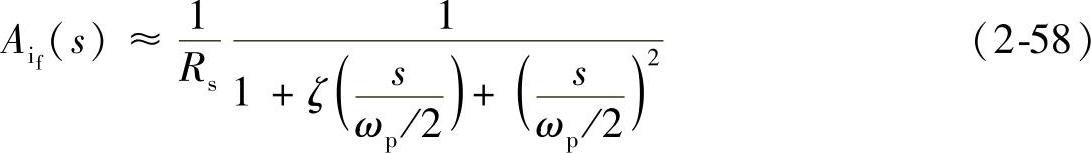
式中，ω_p为电流控制环的极点角频率；ζ=1～1.5。

模型Ⅱ又称为双极点模型。

6.功率级的等效模型

根据如图2-27所示等效功率级是由电流控制环及其负载组成，其框图可表示为图2-30。等效功率级输入信号是电压控制器的输出电压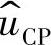，其输出信号为开关变换器的输出电压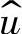，电流控制环的负载Z（s）是由输出电容和负载组成的网络，如图2-31所示，图中R_C是输出滤波电容的ESR，C为输出滤波电容，R为负载，Z（s）的表达式为

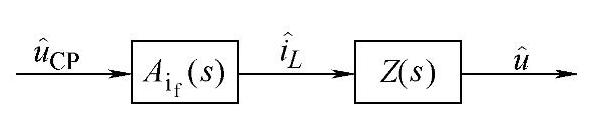
图2-30 等效功率级

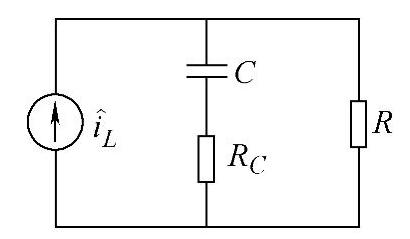
图2-31 等效负载

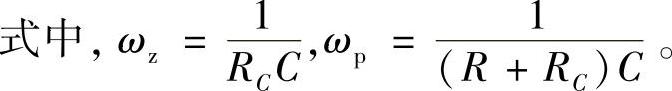
如果用模型Ⅰ近似电流控制闭环传递函数，结合表示Z（s）的表达式，可得到等效功率级的简化模型为

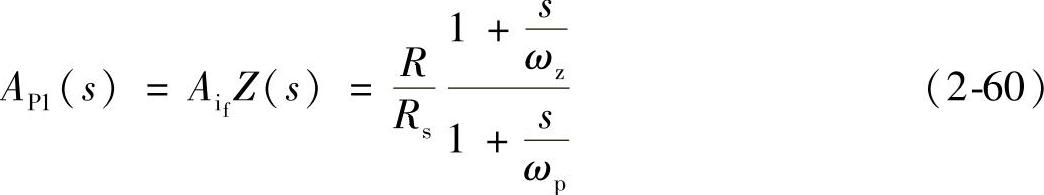
式（2-60）表明，采用电流控制后，电流环与原功率级组成等效功率级为一阶系统。在没有电流控制环时，功率级为二阶系统。采用电流控制环后，系统降阶的原因是，电感电流不再是独立变量而受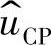控制。

如果用模型Ⅱ近似电流控制闭环传递函数，结合表示Z（s）的表达式，可得到等效功率级的精确模型为

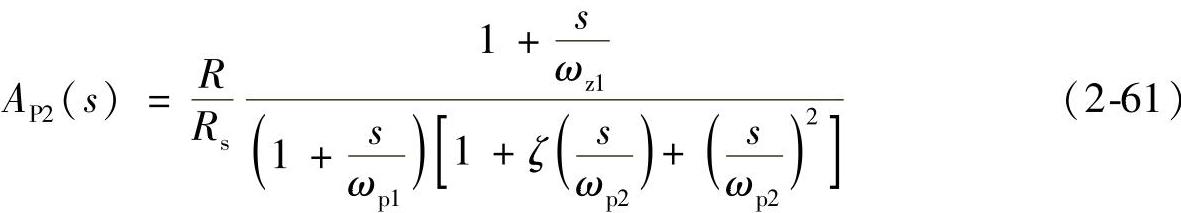
式中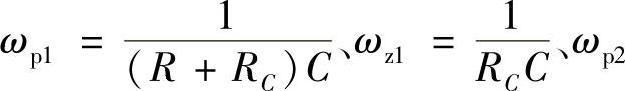，是电流控制环的极、零点。

式（2-61）表明，等效功率级是一个三阶系统。

有了电流控制环的闭环传递函数，可以根据如图2-27所示得出等效单环电压控制系统的原理框图如图2-32所示，图中H（s）为电压采样网络的传递函数；G_U（s）为电压补偿网络的传递函数；A_P（s）为等效功率级的传递函数。

由图2-32可知，电压环的开环传递函数为

T（s）=H（s）G_U（s）A_P（s） （2-62）

式（2-62）是设计电压控制器的基础。

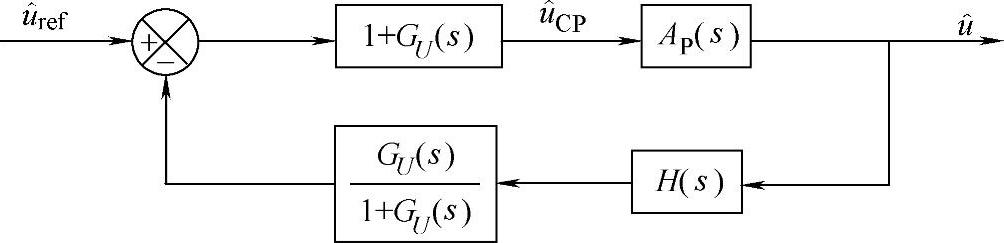
图2-32 等效单环电压控制系统框图

由于等效功率级也是电压控制环的控制对象，因此，简化模型和精确模型都是描述控制对象的传递函数。采用简化模型时，控制对象是单极点型传递函数。采用精确模型时，控制对象是一个三阶系统（其设计可见参考文献[1]）。在本书2.2.2节中已详细介绍了电压控制器的设计方法，这里不再赘述。