Buck变换器是开关电源中最基本的拓扑结构之一，下面以非理想Buck变换器为例分析和研究电压控制型开关调节系统。
设计举例：Buck变换器主电路参数：输入电压Ug=16.0V，滤波电容C=600μF；电容的等效串联电阻RC=7.7mΩ；电感的等效串联电阻RL=55.0mΩ；CCM下动态电感L=42.5μH，负载R=1.0Ω，输出电压U=5.1V，fs=50kHz。
步骤1：绘制控制对象的博德图。利用本书1.1.3节介绍的非理想Buck变换器在CCM下的建模方法为变换器建模，其控制-输出的传递函数为
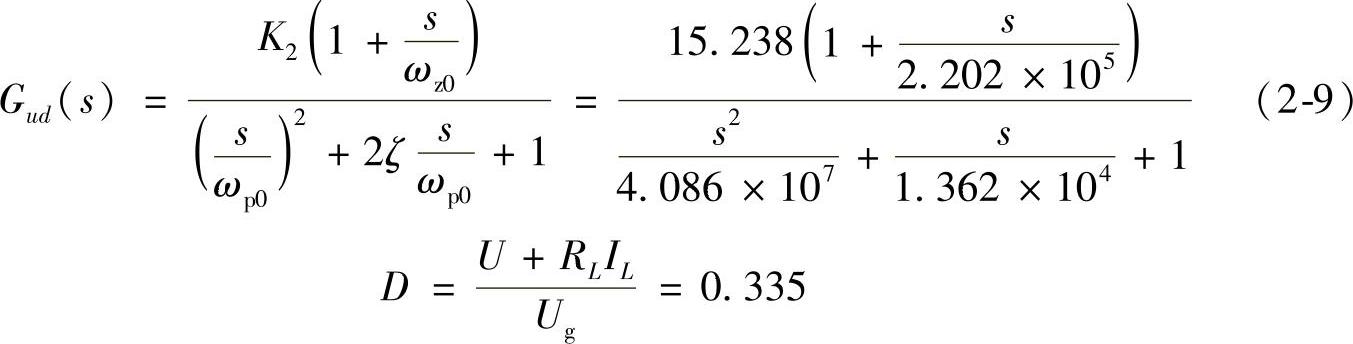
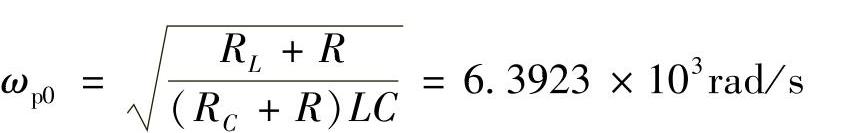
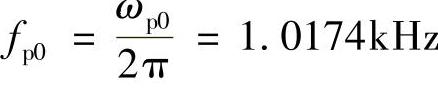
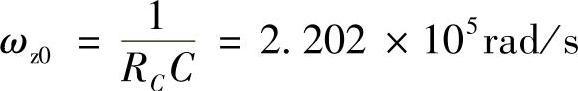
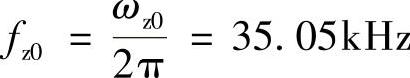
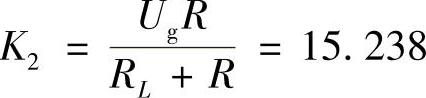
用Pspice10.0仿真软件对系统进行仿真（有关仿真的知识将在后面章节介绍），如图2-15所示是Buck变换器控制-输出传递函数的仿真电路。
用图2-15所示的电路进行仿真从软件中可得到如图2-16所示的控制-输出的幅相频率特性仿真曲线，其中图a是幅频特性曲线，图b是相频特性曲线。
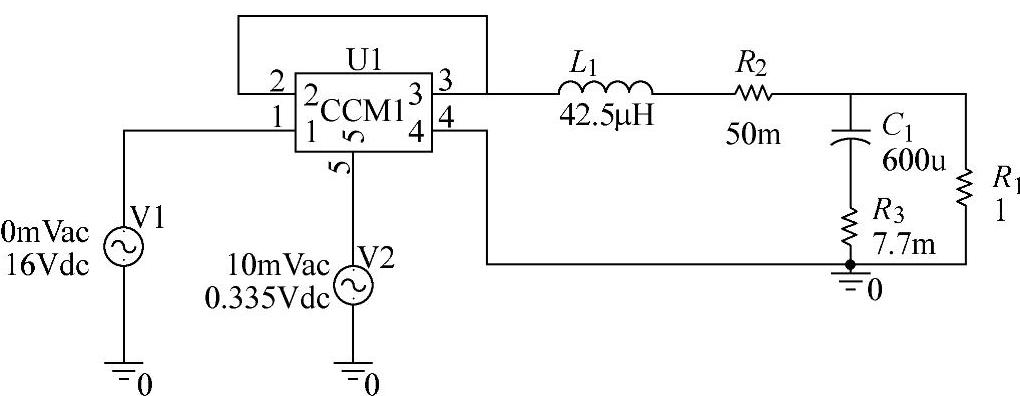
图2-15 Buck变换器控制-输出传函仿真电路（CCM）
由仿真和实验测得穿越频率约为fc=4.089kHz，相位裕量φm=13.9°。从表面上看系统是稳定的，但若系统中的参数稍有变化，系统就会变不稳定。
步骤2：设计电压采样网络。搭建的实验样机采用控制芯片为UC3825，芯片的PWM中锯齿波的幅值为VM=2.8V，采样网络为H（s）=Uref/U=5.1/5.1=1.0。
步骤3：计算系统开环传递函数。根据图2-14的系统框图得系统的开环传递函数为
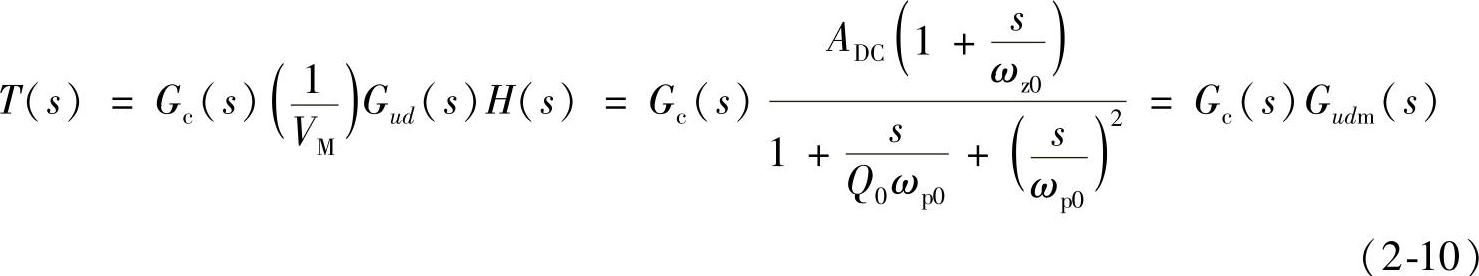
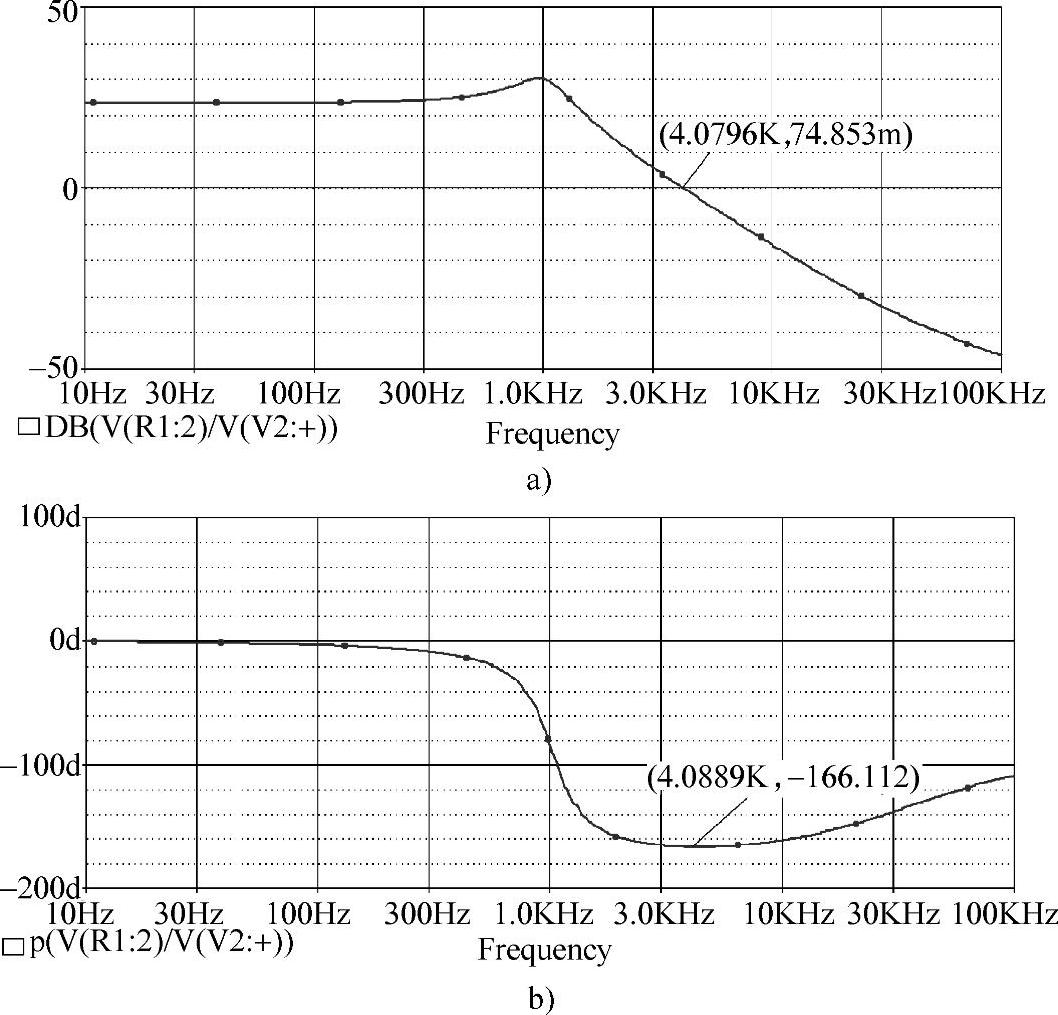
图2-16 Buck变换器控制-输出传函仿真曲线（CCM）
a）幅频特性 b）相频特性
式中，ADC=K2GM（s）H（s）
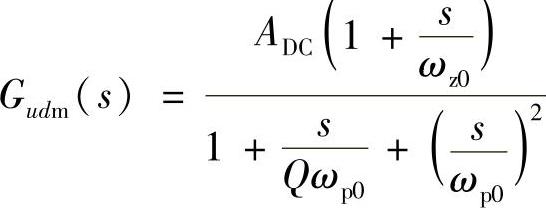
假设采用单位增益的反相放大器作为补偿网络，则系统的开环直流增益为ADC=K2GM（s）H（s）=5.44。系统的稳态误差为1/（1+ADC）=15.53%，显然工程上不允许。为此要设计一合理的控制器，使系统能够稳定运行。
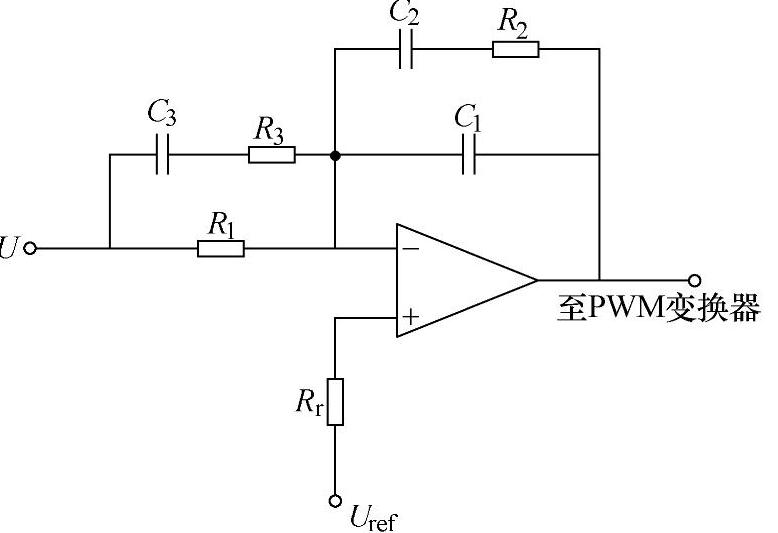
图2-17 双极点-双零点补偿网络
步骤4：确定补偿网络，并绘制三条对数频率特性曲线。由式（2-9）可知，Buck变换器控制-输出的传递函数具有一个零点和两个双重极点，根据参考文献[1]对补偿网络的设计分析，在此宜采用如图2-17所示的双极点-双零点补偿网络。
查表2-3双极点-双零点补偿网络传递函数及有关参数的公式如下[1]：
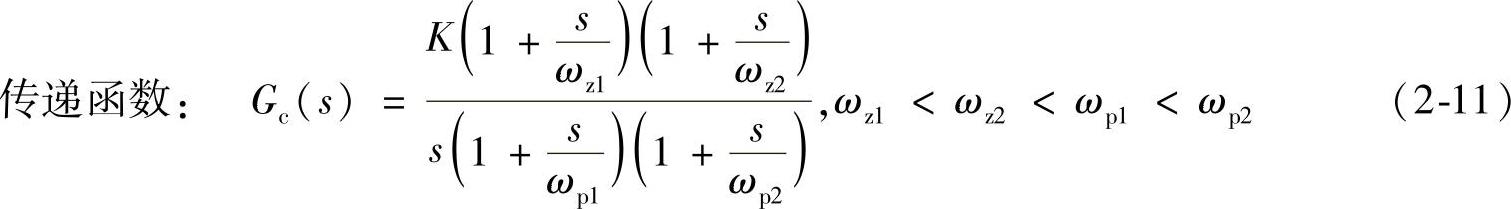
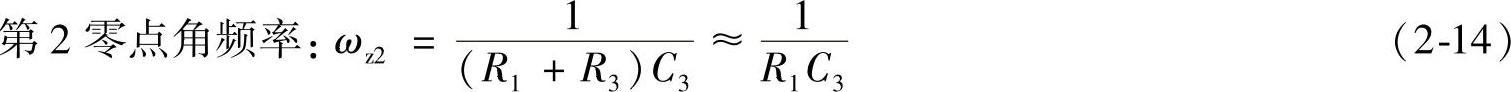
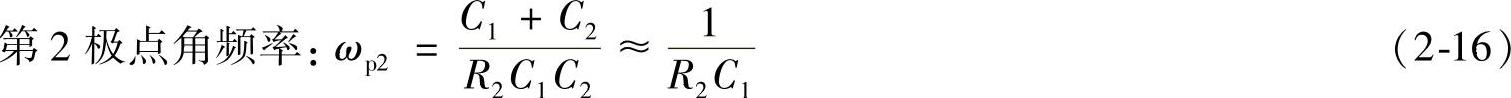
三条对数频率特性曲线如图2-18所示。双极点-双零点补偿网络在直流处提供了一个极点，因此其稳态误差等于零，它的第1极点（ωp1）是用来抵消输出电容的串联电阻ESR的高频零点，第2极点（ωp2）用来保证开环传递函数有一个较好的相位裕量和增益裕量，对高频干扰有很好的抑制作用。
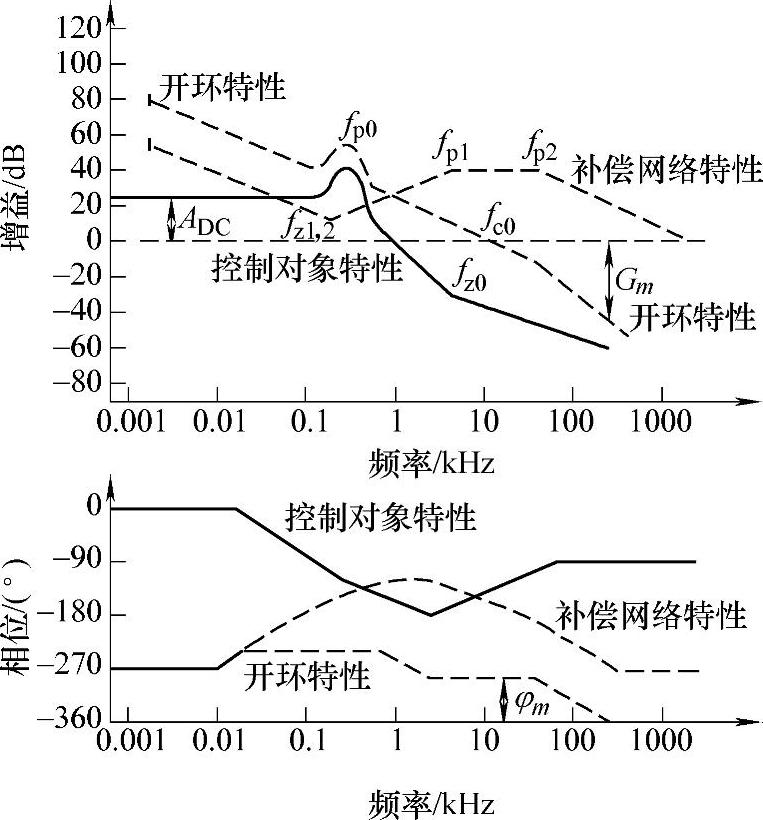
图2-18 三条对数频率特性曲线
步骤5：计算穿越频率。为了提高穿越频率，设加入补偿网络后开环传递函数的穿越频率是开关频率的1/6左右，即
fc=fs/6=50kHz/6=8.33kHz （2-17）
步骤6：确定补偿网络的零点角频率ωz1、ωz2和极点角频率ωp1、ωp2。用补偿网络的一对零点ωz1、ωz2来抵消控制对象中的双重极点引起的相位滞后。通过这一对零点的补偿后，在高于双重极点频率的频段，开环传递函数的幅频特性是以斜率为-20dB/dec下降。有文献介绍，两个零点频率应小于截止频率，其中第1零点应小于功率级的自然谐振频率，即
fz1＜fp0 （2-18）
因为，fc=8.33kHz，所以取第1零点频率为
fz1=700Hz （2-19）
又由于第2零点频率为
fz1＜fz2＜fc （2-20）
所以，取fz2=4.0kHz。
用fp1抵消ESR零点出现的最低频率，则有
fp1=fz0=35.05kHz
将fp2设置在稍高于穿越频率处，参考文献[32]给出的公式为
fp2≥1.5fc=1.5×8.33kHz=12.50kHz
步骤7：确定补偿网络平坦段的增益A1（G1）和A2（G2），如图2-19所示。(www.daowen.com)
在第一个曲线平坦频段，fz1＜f＜fz2，传递函数近似表达式为
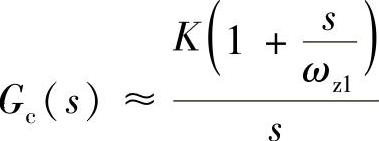
幅度的近似表达式为
用分贝表示为
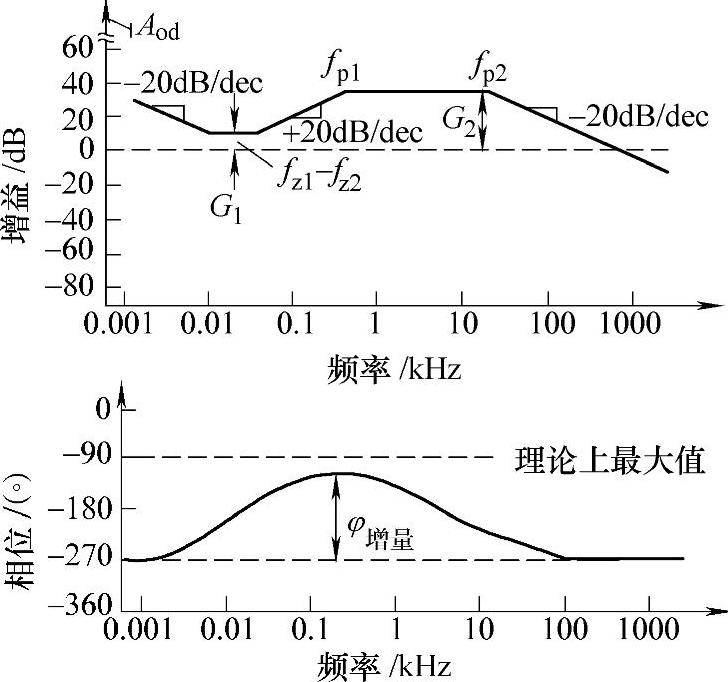
图2-19 双极点-双零点补偿网络频率特性曲线
G1=20lgA1 （2-22）
在补偿网络中，当fz1＜f＜fz2时，相当于C1、C3开路，C2短路，所以C2＞＞C1且C2＞＞C3，C2的容值最大。
第二个曲线平坦段fp1＜f＜fp2，近似表达式为
因为C2＞＞C1，且R1＞＞R3，幅度的近似表达式为
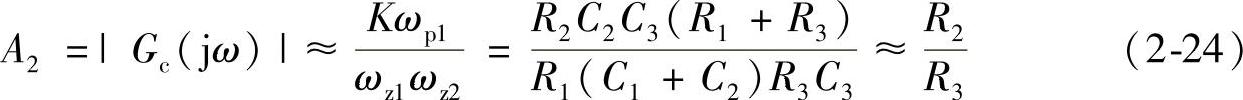
补偿网络在fp1＜f＜fp2频段，相当于C1开路，C2，C3短路，用分贝表示为
G2=20lgA2 （2-25）
对于补偿网络，当频率处在fp1＜f＜fp2，对数幅频特性处于第二个平坦段，其幅值用A2表示，用G2表示分贝值，G2=20lgA2。所以，当ω=ωc时，补偿网络对数幅频特性为一个常数G2（dB）。
在穿越频率处，开环传递函数对数幅频特性为0dB，所以有
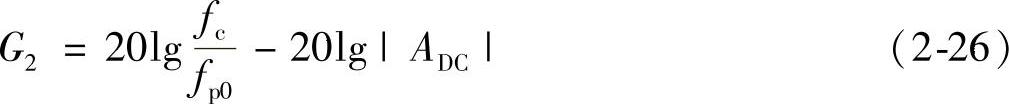
在图2-19中，两个平坦频段之间的对数幅频特性以+20dB/dec的斜率上升，G1、G2应满足如下关系：
则A1计算公式应为
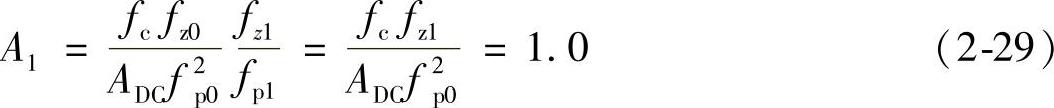
步骤8：补偿网络的参数设计。
取R1=20kΩ，根据式（2-21）有
R2=A1R1=1.0×20kΩ=20kΩ （2-30）
取标称电阻R2=20kΩ。
根据式（2-24）有
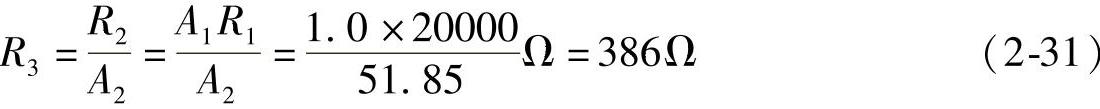
取标称电阻R3=390Ω。
根据式（2-20），fp2≥1.5fc，为了简化计算取近似为fp2=fc，当C2＞＞C1时，根据式（2-16），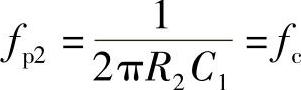
，得第2极点电容的计算公式如下：
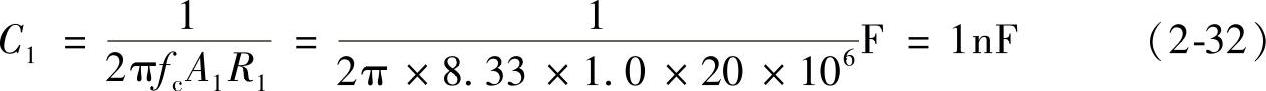
取标称电容C1=1nF。
根据式（2-13）
得第1零点电容计算公式如下：
取标称电容C2=15nF。
根据式（2-14）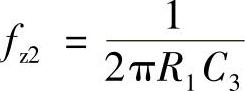
得第1极点电容或第2零点电容计算公式如下：
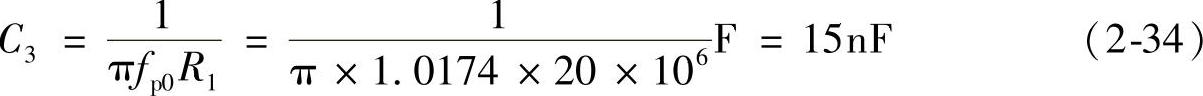
取标称电容C3=15nF。
经计算由图2-17所示的补偿网络采用的实际电容和电阻的参数：R1=20kΩ，R2=20kΩ，R3=390Ω，C1=1nF，C2=15nF，C3=15nF。
步骤9：校验。
用Pspice10.0仿真软件对电压控制型调节系统进行环路增益仿真，图2-20所示为软件中电压控制型调节系统的仿真电路图。图2-21所示为电压控制型调节系统环路增益的幅频特性和相频特性的仿真曲线，图a是幅频特性曲线，图b是相频特性曲线。
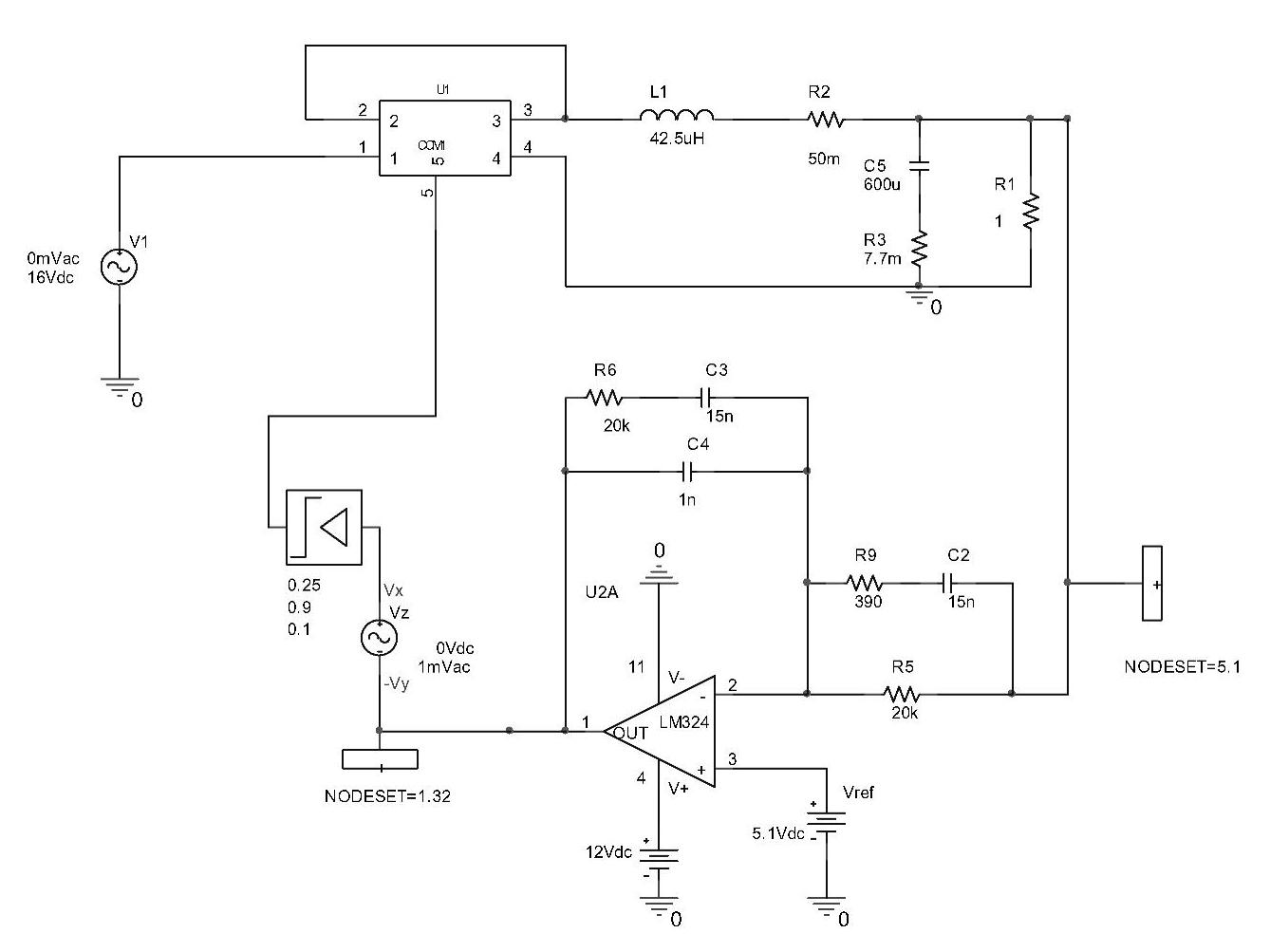
图2-20 电压控制型调节系统环路增益的仿真电路
仿真实验测得系统的穿越频率为fc=6.0287kHz，相位裕量φm=44.654°。这表明控制器设计是合理的，系统是稳定的。
以上基于非理想Buck变换器，在考虑电感等效串联电阻和电容等效串联电阻的情况下，研究了电压控制型开关调节系统的建模、控制器设计、系统仿真。
仿真结果验证了控制器设计的合理性。
图2-21 电压控制型调节系统的开环频率特性曲线
a）幅频特性 b）相频特性
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
