1.控制器设计步骤

一般开关调节系统的设计步骤：①根据用户要求确定技术指标；②主电路设计，即根据技术指标和设计要求选择主电路拓扑结构，并设计其参数；③对主电路建立交流小信号模型，分析其电气特性；④根据系统的静态和动态技术指标和主电路的电气特性设计控制器。这也是本节主要研究的内容。

由于开关调节系统是一种特殊的自动控制系统，因此其控制器的设计思路与自动控制系统的设计思路相似，主要的研究工具也是博德图，即开环对数频率特性的渐近线。

开关调节系统的控制器设计步骤为[1]：①将时域技术指标转化为相应的频域参数；②在频域内分析主电路的典型传递函数，画出其开环对数频率特性；③根据主电路典型传递函数和频域参数，设计和校验满足技术指标且与主电路相匹配的控制器。

2.理想开环传递函数的频率特性

由于系统的开环传递函数的博德图能够确切反应系统的稳定性、稳定裕量，且还能大致衡量闭环系统的性能，因此在定性分析闭环系统性能时，一般给出系统的理想开环传递函数的频率特性如图2-11所示。

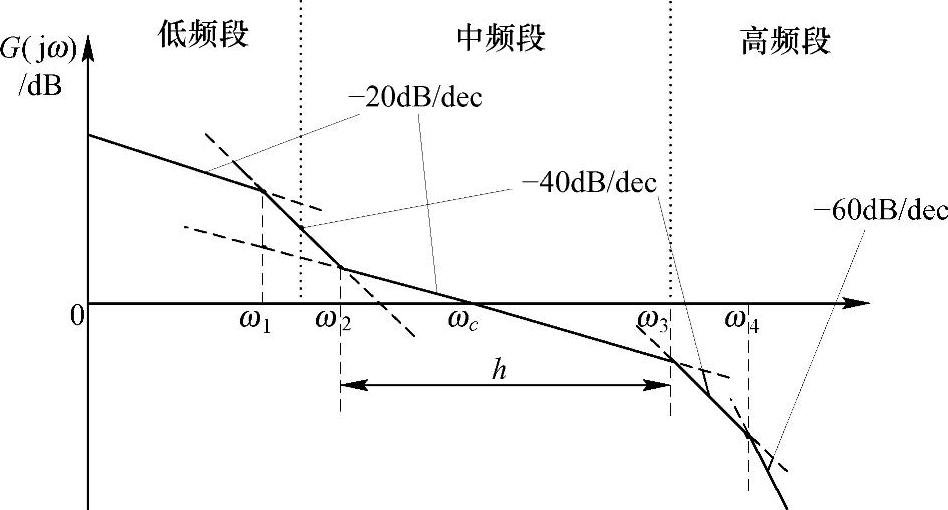
图2-11 系统理想开环传递函数的频率特性曲线

通常将图2-11所示的频率特性大致分成低、中、高三个频段，根据其中三个频段的特征可判断系统的性能，其中：

（1）低频段

低频段主要影响系统的稳态性能，其形状直接反映系统包含积分环节的个数和直流增益的大小，对于开关调节系统，理想的低频特性是直流增益无限大、以-20dB/dec^[1]的斜率下降。符合理想条件时，系统的稳态误差等于零。

（2）中频段

中频段的宽度h与系统的动态稳定性相关。宽度h愈大，相位裕量φ_m愈大。穿越频率ω_c与系统的上升时间t_r、调节时间t_s以及超调量σ等动态性能指标密切相关。穿越频率ω_c愈大，系统的响应速度愈快但超调量σ增加。中频段大致是指，幅频特性以-20dB/dec斜率下降并穿越0dB线的频段。但对于开关调节系统，过高的穿越频率ω_c可能导致高频开关频率及其谐波和寄生振荡引起的高频分量得不到有效的抑制，系统仍然不能稳定的工作。为此，在理想的中频特性中，需附加一个以-40dB/dec斜率下降的频段，达到降低中频增益以限制过高的穿越频率ω_c。由于这个附加频段位于中频的起始阶段，必然引起一定附加相位滞后。所以，附加频段的宽度不能太大，否则会影响系统的稳定性。

（3）高频段

一般高频段距穿越频率ω_c较远，开环传递函数对数幅频特性‖T（jω）‖＜＜1，对系统的动态性能影响不大，但它反映系统对高频干扰信号的抑制能力。高频段幅频特性衰减越快，系统的抗干扰能力越强。对于开关调节系统，理想高频特性应以-40dB/dec斜率下降。如果高频段的幅频特性斜率的绝对值增加，意味着控制器的结构复杂，给设计和调试带来不必要的麻烦。

3.控制器的频域设计思路

为了便于设计，把补偿网络和电压采样网络的总和称为电压控制器，把电压控制器以外的环节称为控制对象。用本书第1章介绍的方法对控制对象，即主电路建立交流小信号模型，例如根据本书1.3.5小节的例子中Buck变换器的参数进行仿真，可得到相应主电路控制-输出传递函数的对数频率特性如图2-12所示，而希望获得系统的开环频率特性如图2-13所示。将两条已知的渐近线相减，由各对应点差值所获得的新的渐近线便是所要设计控制器的特性渐近线。

值得一提的是：不同的控制对象会得到不同的控制器频率特性渐近线；同一控制对象而设计指标不同也会得到不同的控制器频率特性渐近线；即使是同一对象同一控制器频率特性渐近线，但电路的参数不同系统的性能也会不同，因此，设计控制器是较复杂的工作。值得庆幸的是参考文献[32]总结了已有的成果，给出了常用补偿网络相应的性能（见表2-1）和控制对象与补偿网络的匹配表（见表2-2），设计者可根据控制对象容易地找到较合适的补偿网络。

表2-1 常用补偿网络相应的性能

表2-2 控制对象与补偿网络的匹配表

为了方便读者，本书将各种常用的补偿网络的传递函数、频率特性、各参数（零极点等）的求解公式、对应的电路列于表2-3。(www.daowen.com)

4.电压采样网络

前面已定义了控制器是由补偿网络和采样网络组成的，根据图2-10很容易得到电压控制型的开关调节系统的框图，如图2-14所示。

表2-3 常用补偿网络传递函数、频率特性和对应电路

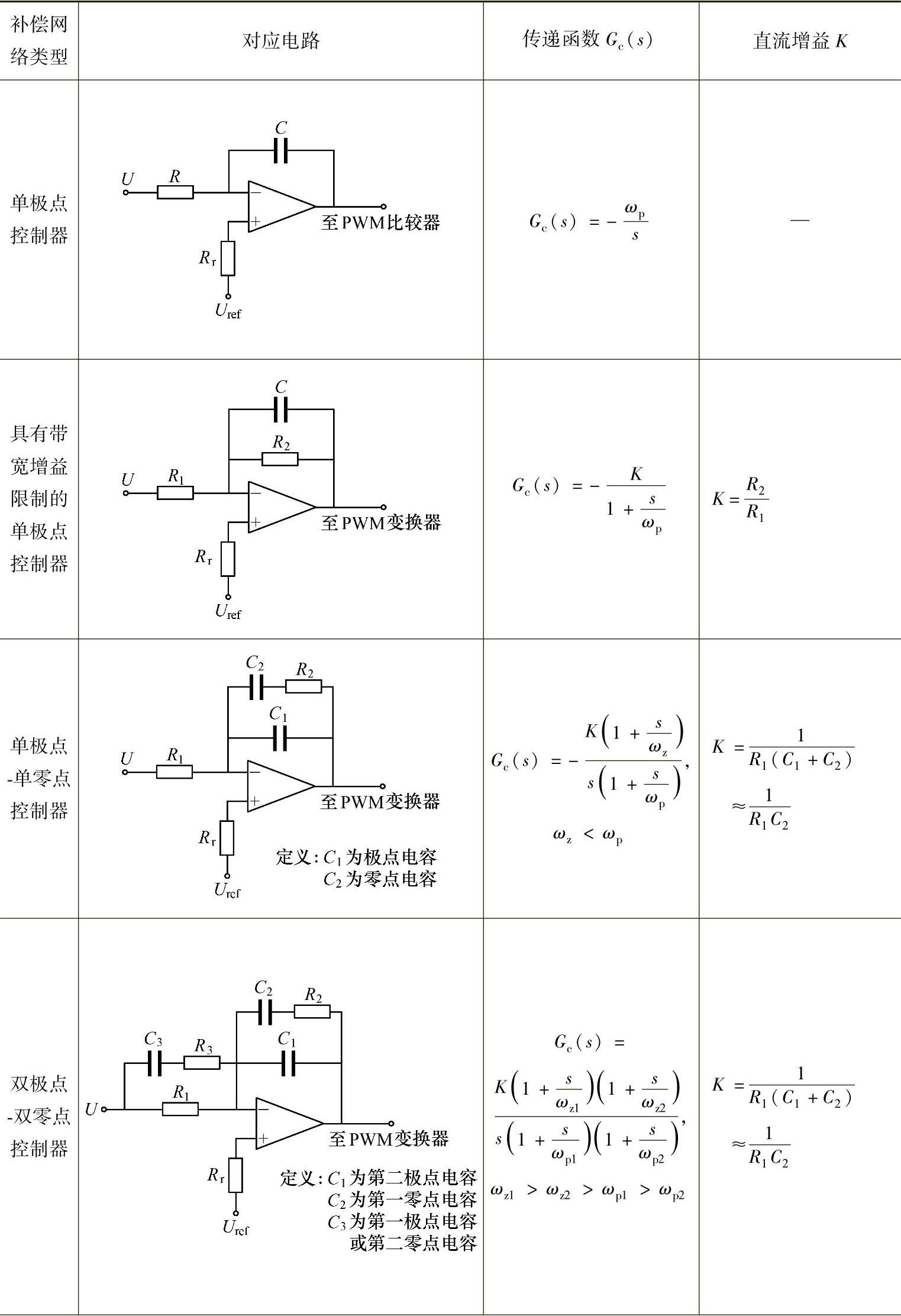
（续）

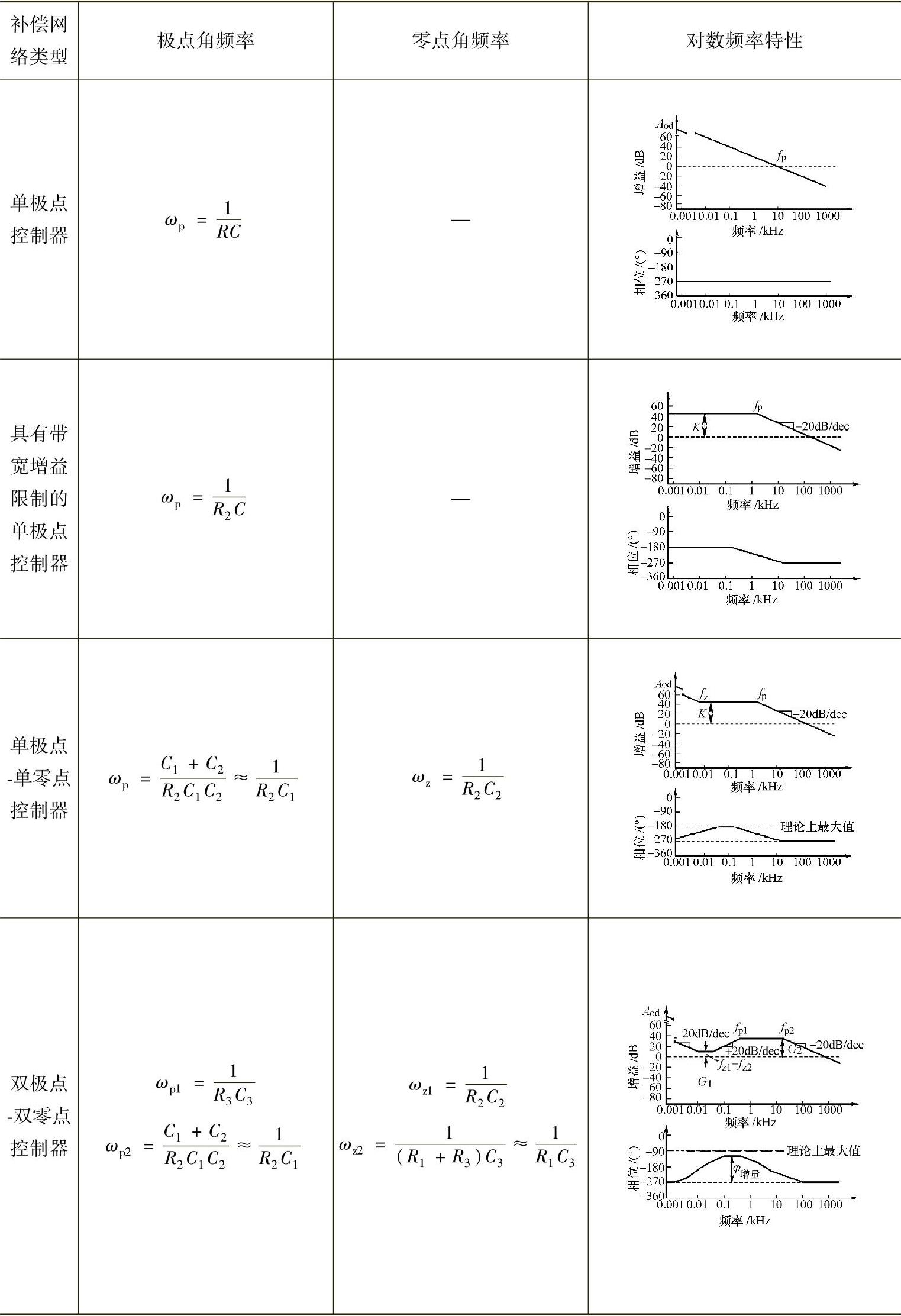
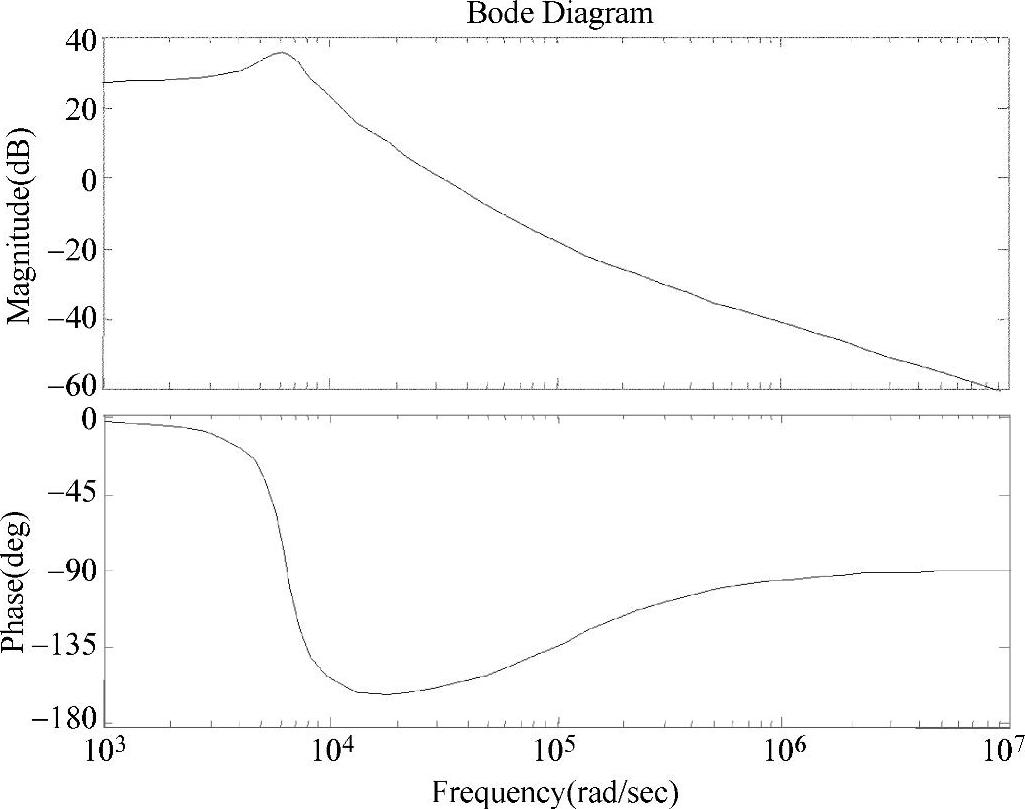
图2-12 1.3.5小节中举例的Buck变换器 控制-输出传函仿真频率特性曲线

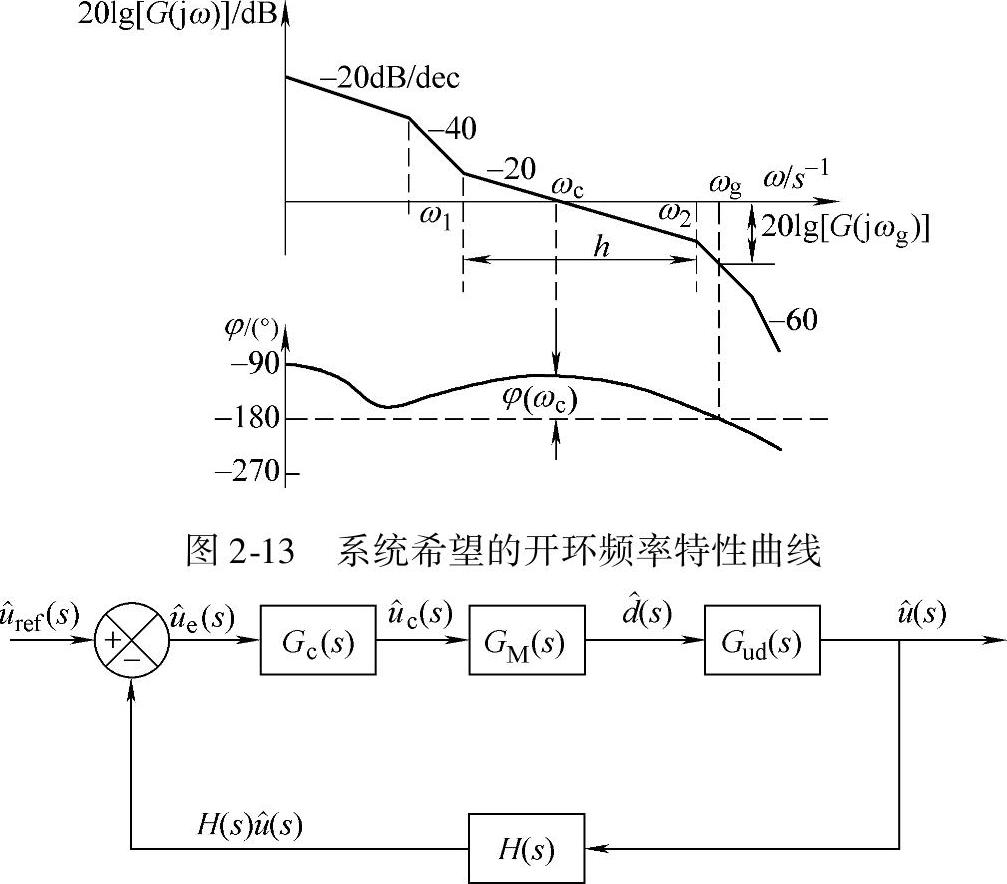
图2-14 电压控制型开关调节系统框图

图2-14中各符号的定义如下：

参考电压象函数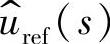： 电压补偿网络的传递函数：G_c（s）

误差量象函数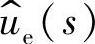： 电压补偿网络的输出量象函数：u_c（s）

占空比象函数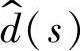： PWM的传递函数：G_M（s）（=1/V_M）

输出电压象函数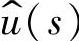： PWM中锯齿波的幅值：V_M

控制-输出的传递函数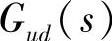： 电压采样网络的传递函数：H（s）（=K）

由图2-14可得系统的闭环传递函数为

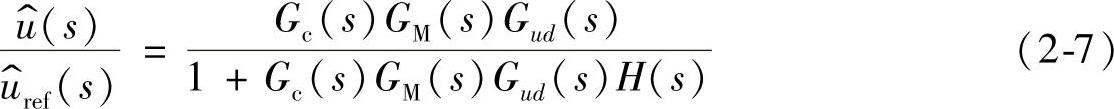
实际设计时，为消除稳态误差，一般低频段，尤其在直流频率点，开环增益|1+G_c（0）G_M（0）G_ud（0）H（0）|≥1，即在直流频率点处系统为深度负反馈系统。当系统满足深度负反馈时，闭环传递函数可近似的改写为

上式表明：稳态时，当参考电压U_ref给定，输出电压U仅取决与电压采样网络的传递函数。也就是说，在稳态时，输出电压的大小只与参考电压和采样网络有关，而与补偿网络和主电路等无关。因此，电压采样网络应在稳态条件下设计，也即采样网络中的电容相当于开路，电感相当于短路。

不同类型的开关调节系统，其电压采样网络的拓扑结构和设计方法也不同。根据输出的不同，开关调节系统可分为单路输出和多路输出；根据输入端和输出端是否电气隔离，开关调节系统又分为电气隔离型和无隔离型。但常用的开关调节系统中主要为无隔离型电压采样网络、多路输出的电压采样网络和隔离型电压采样网络等三种基本采样网络。关于电压采样网络的设计在参考文献[1]有详细的介绍，此处不赘述。