PWM调制器的数学模型及时域波形分析

如图1-56所示为PWM的数学模型示意图。图中，u_c（t）表示占空比的控制信号，u_saw（t）是锯齿波信号，周期为T，即开关频率的周期，峰峰值为V_M。设u_c（t）在一个周期T内变化很小，则当t∈[nT，（n+1）T]时，u_c（t）=u_c（nT）。这种处理的实际意义相当于用一个单位冲击序列在t=nT（n=0，1，2…）时，对u_c（t）信号进行采样和保持。所以，在图1-56b中，用一个采样开关δ_T和零阶保持器G_zoh（s）表示这个过程。

锯齿波u_saw（t）的一般表达式

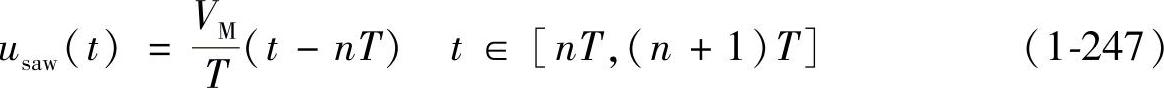
习惯上，峰峰值用V_M表示，本书与习惯一致。

在PWM中，当t=T_on+nT时，u_saw（t）=u_c（nT），令d（nT）=T_on/T，则有

d（nT）=u_c（nT）/V_M （1-248）

式中，V_M是u_saw（t）信号的最大幅值。

对式（1-248）两边取z变换得

D（z）=U_c（z）/V_M （1-249）

上式是PWM的离散数学模型。(https://www.daowen.com)

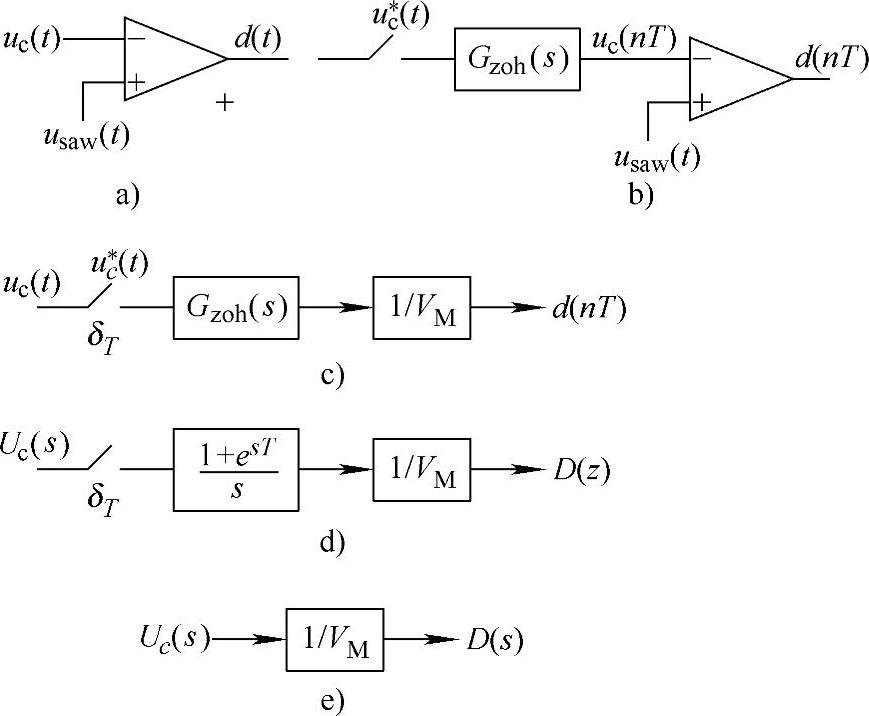
图1-56 PWM的数学模型示意图

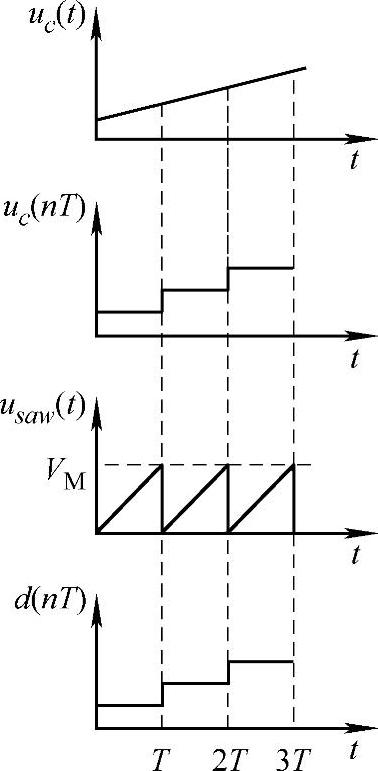
图1-57 图1-56各主要点时域波形

上述处理过程可用图1-56进行说明。如图1-56a所示是一般的PWM；如图1-56b所示是对u_c（t）信号采样保持后再与u_saw（t）进行比较；如图1-56c所示是PWM的时域数学模型；如图1-56d所示是PWM的离散数学模型；如图1-56e所示是PWM的连续数学模型。图1-56a、b、c中各点的时域波形如图1-57所示。

如果对式（1-248）进行如下处理，令nT→t，则式（1-248）变为连续的函数，并取拉普拉斯变换得D（s）=U_c（s）/V_M，PWM的传递函数为

上式为PWM的交流小信号数学模型。