DCM下的交流小信号等效电路分析

如图1-50所示为已建立的非Buck变换器在DCM下的交流小信号等效电路。与CCM一样为了进一步定量分析非理想Buck变换器在DCM下的低频动态特性，可根据如图1-50所示的等效电路建立相应的交流小信号s域的等效电路，如图1-51所示。

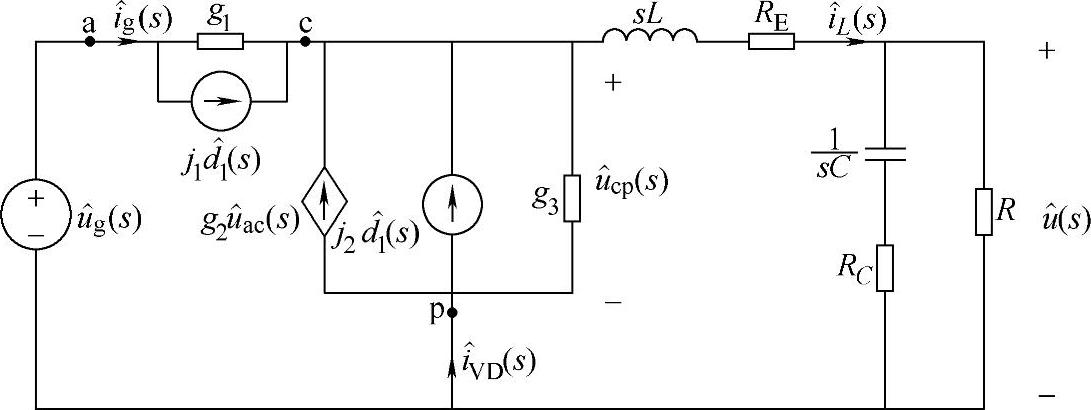
图1-51 非理想Buck变换器在DCM下交流小信号s域等效电路

根据如图1-51所示的等效电路可导出非理想Buck变换器在DCM下的传递函数。

1.输出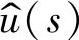电压对输入电压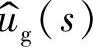的传递函数

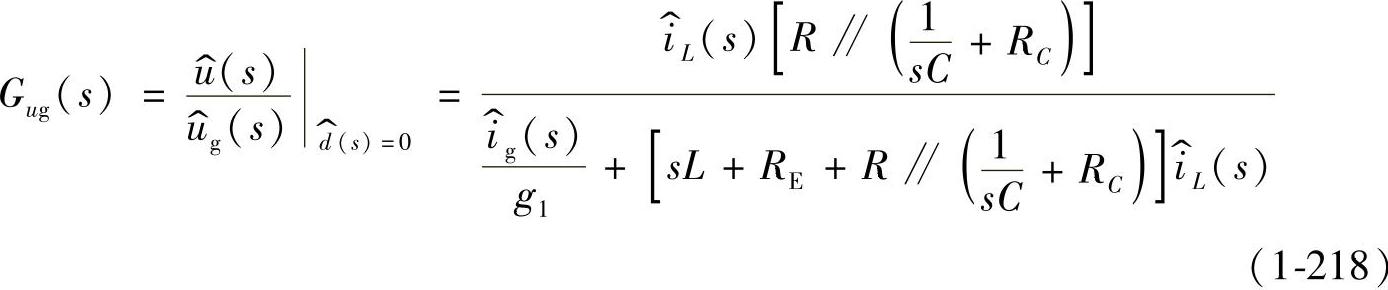
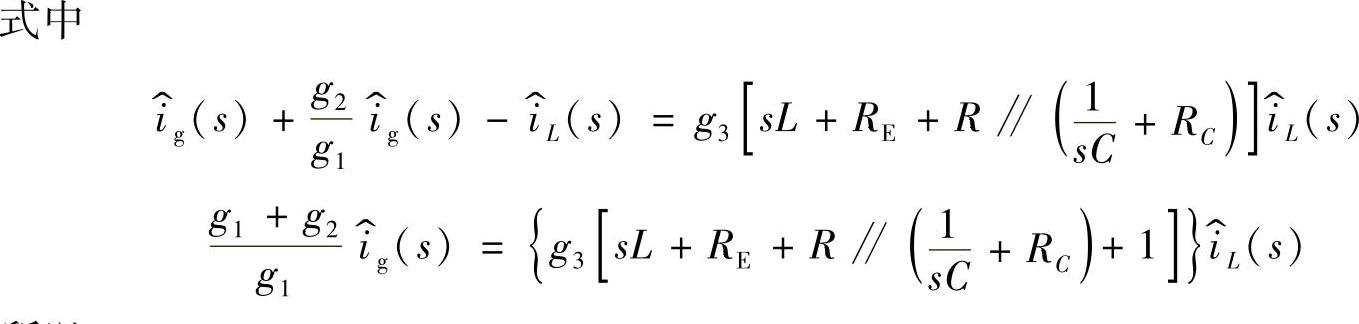
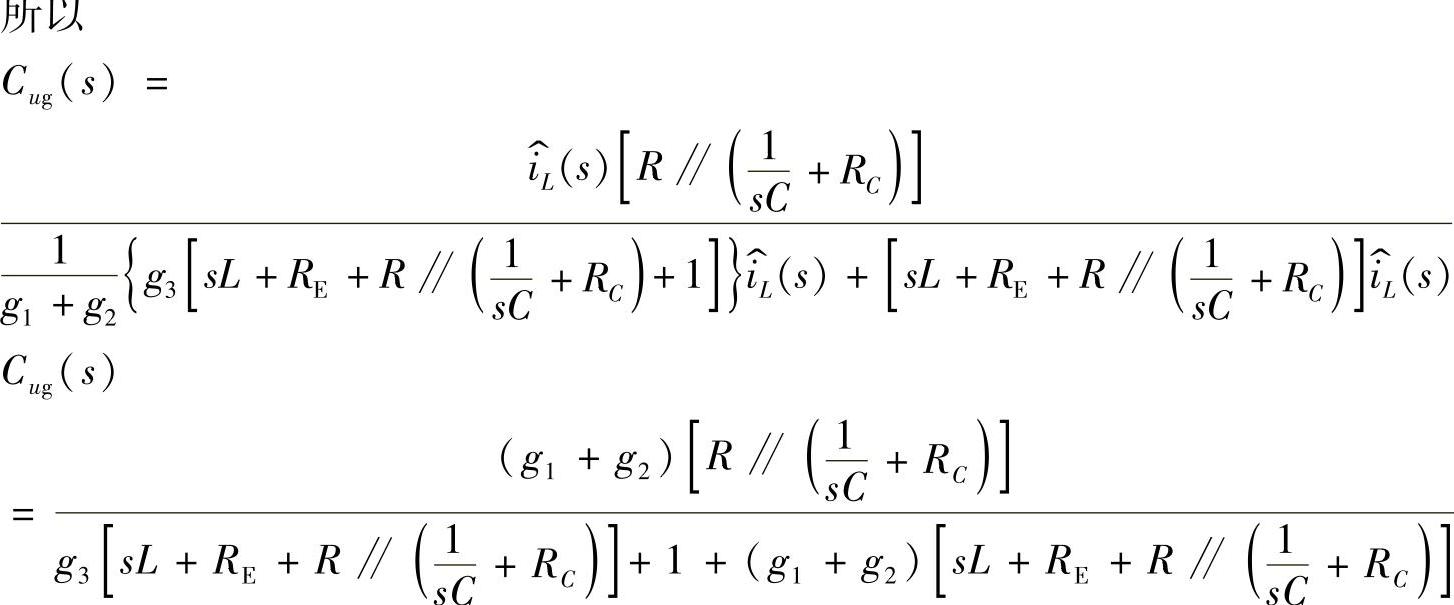
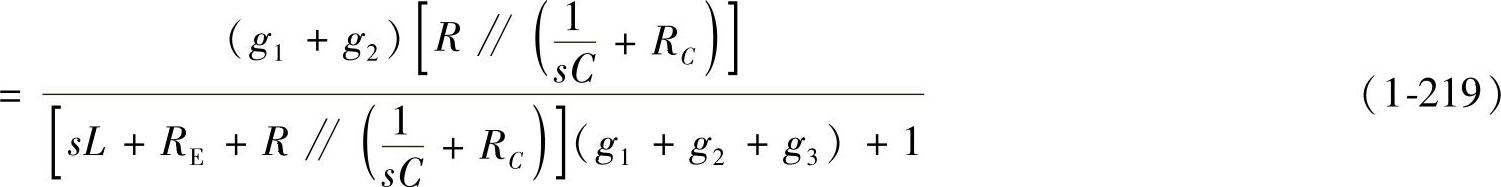
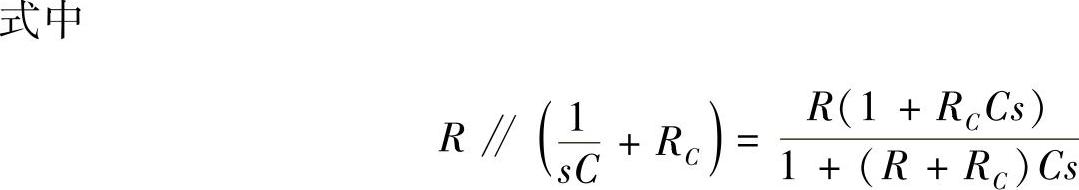
式中，各参数如下：

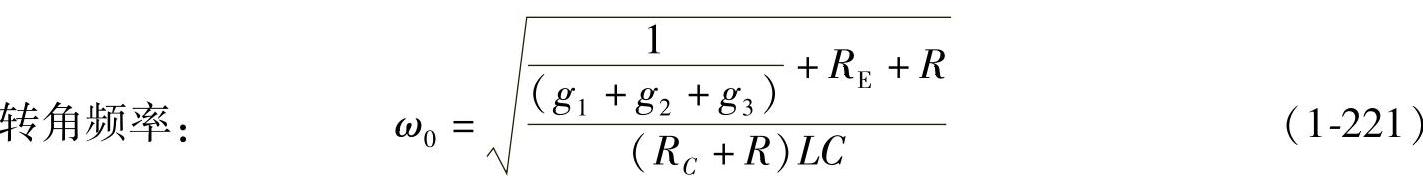
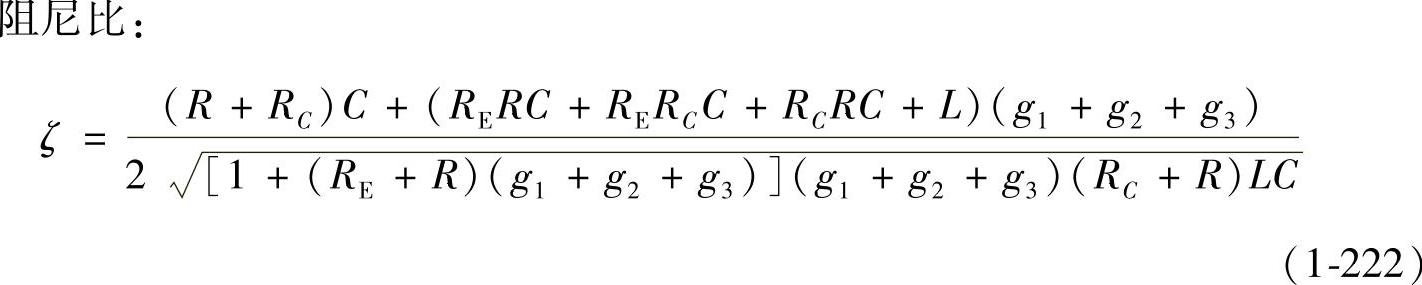
品质因数：

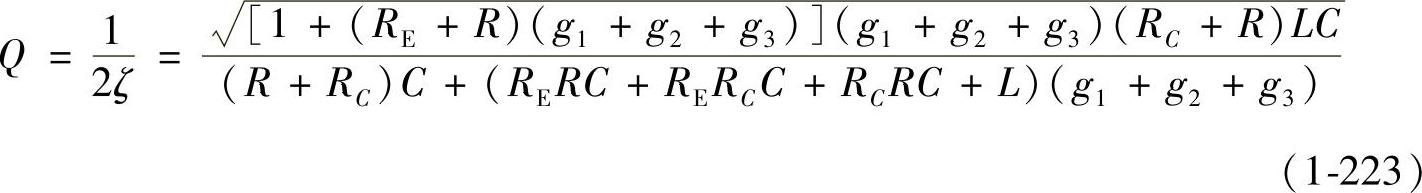
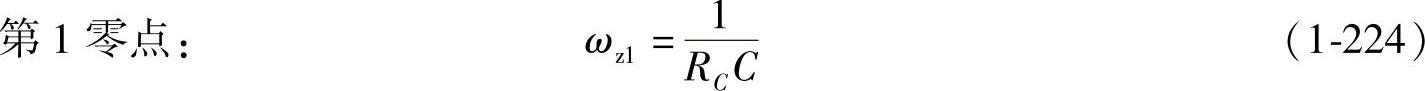
2.输出电压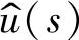对控制变量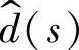的传递函数

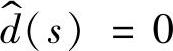时的等效电路如图1-52所示，控制-输出的传递函数为

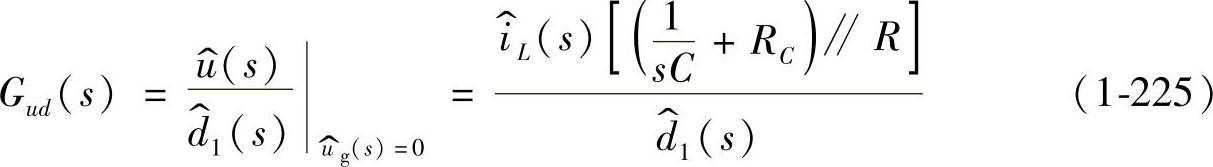
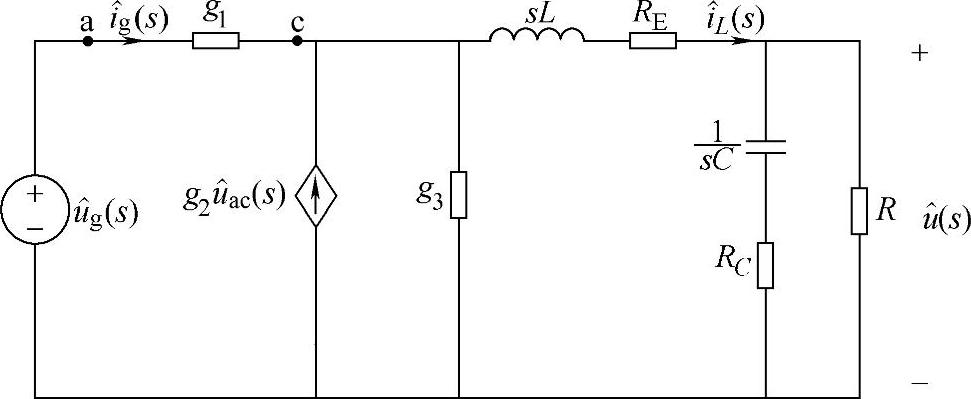
图1-52 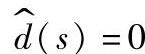时的等效电路

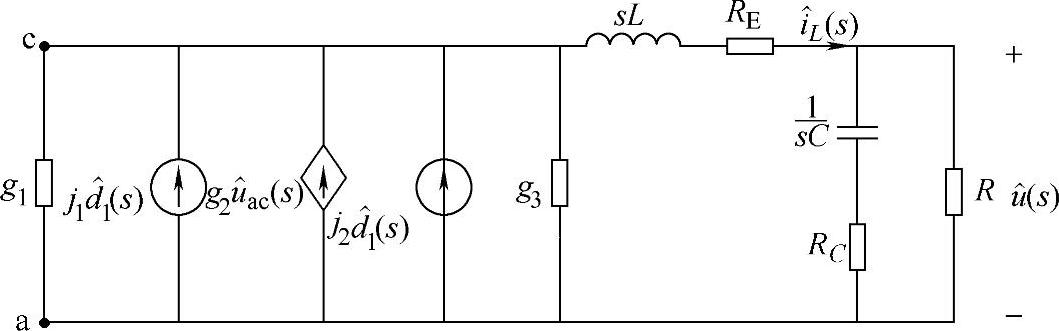
图1-53 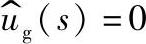时的等效电路

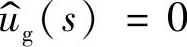时的等效电路如图1-53所示，对于图1-53中的节点c有

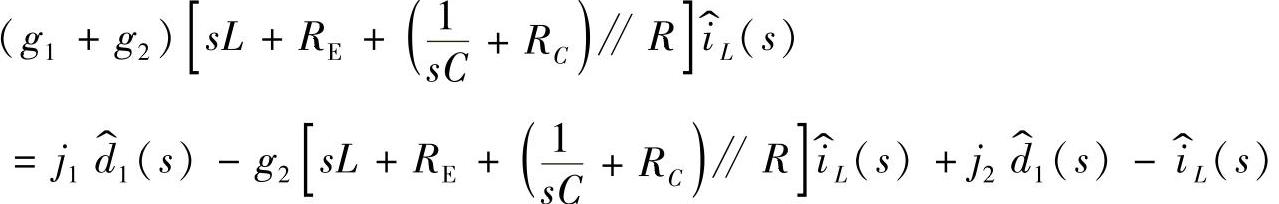
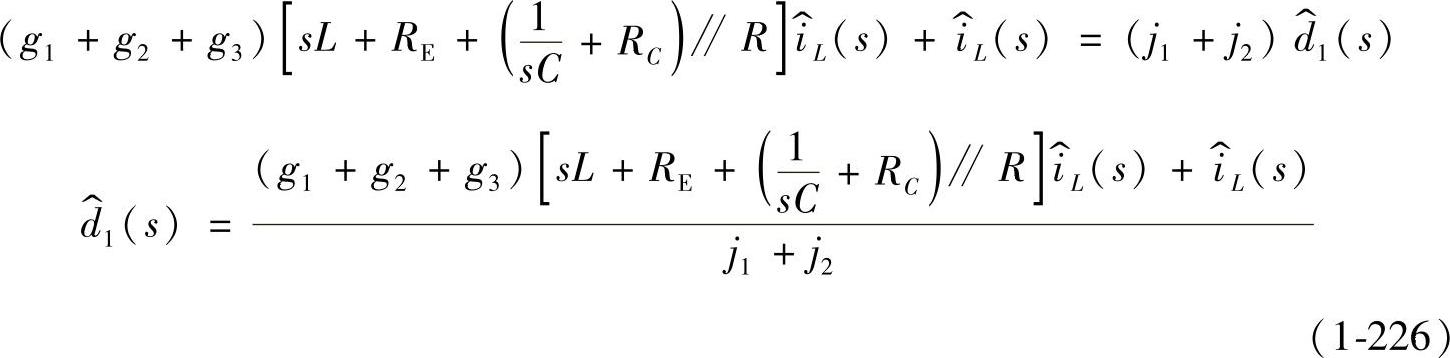
3.开环输入阻抗Z（s）

令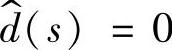则有

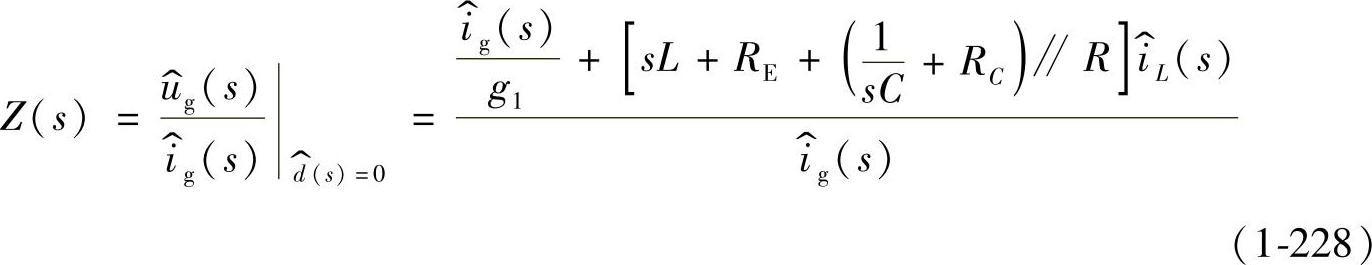
式中

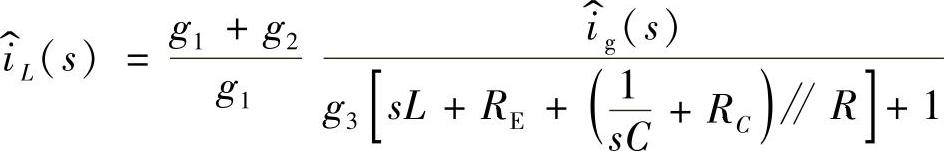
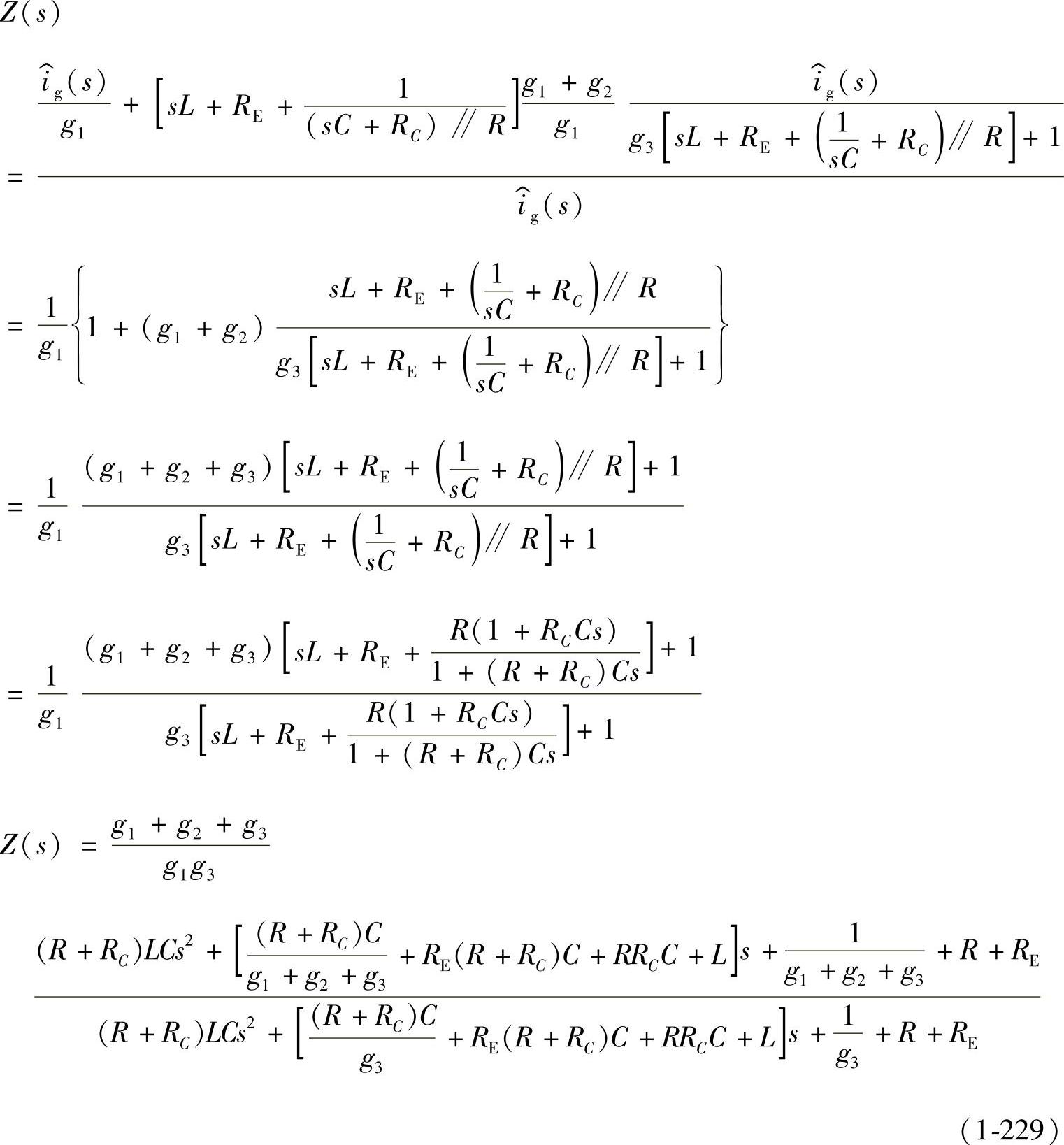
4.开环输出阻抗Z_out（s）

令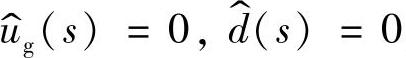，则有

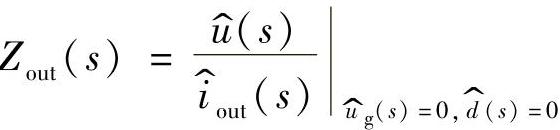
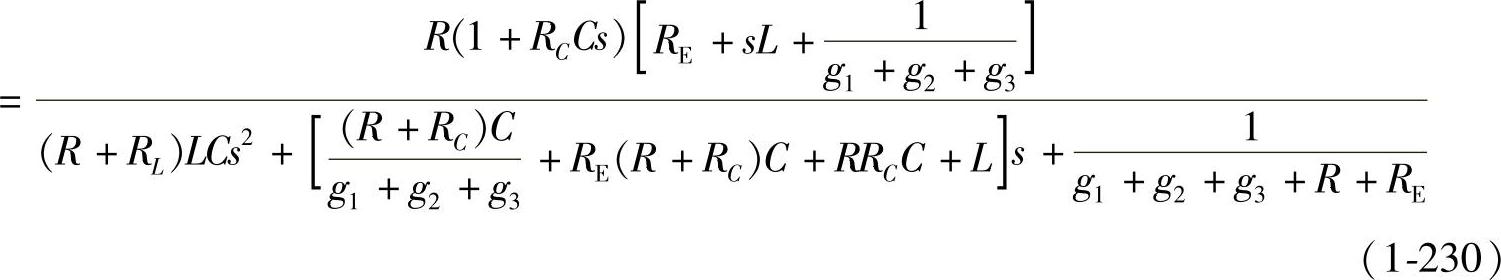
令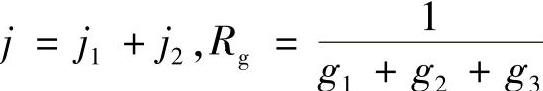，则图1-53可简化为图1-54。

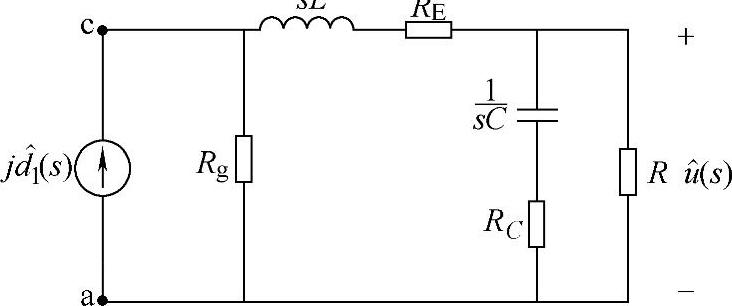
图1-54 图1-53的简化图(https://www.daowen.com)

由于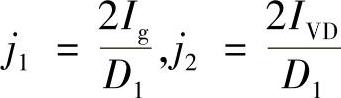，所以有

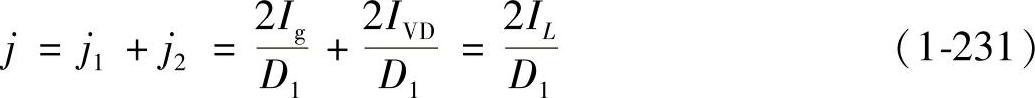
假设R_E在直流分析中可忽略，则有

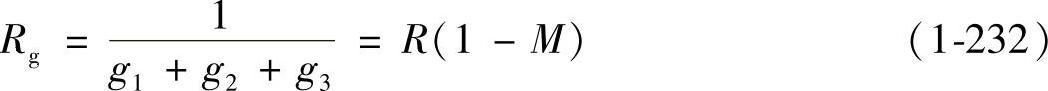
由图1-54所示可得到控制-输出传递函数为

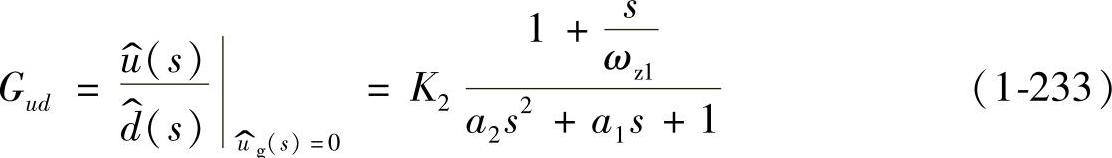
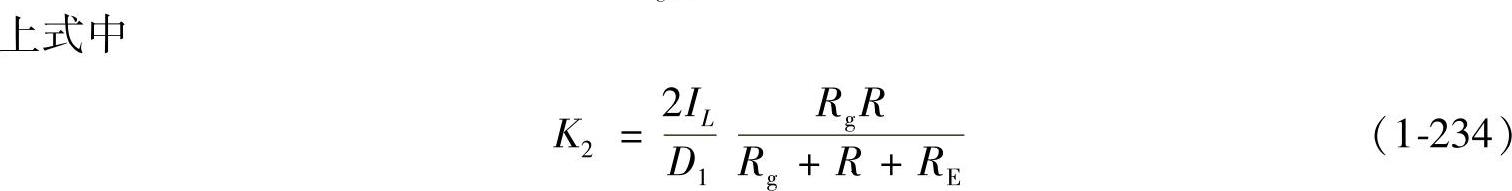
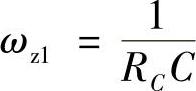
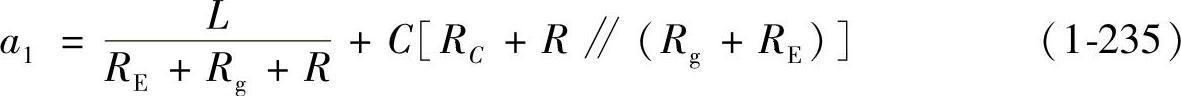
当R_C=0，R_E=0，R_VD=0，U_VD=0，R_on=0，可得

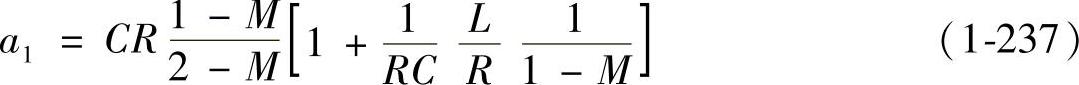
式（1-237）括号中的第二项可以写成

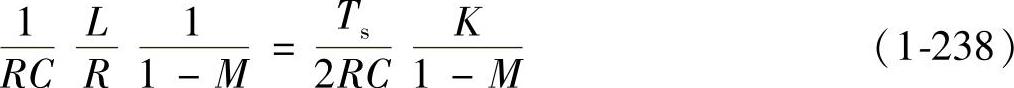
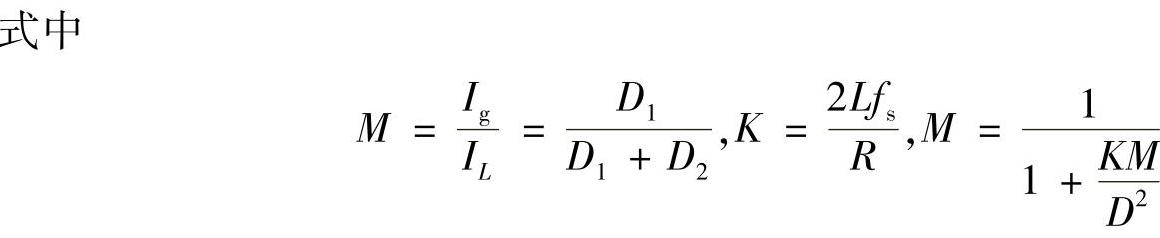
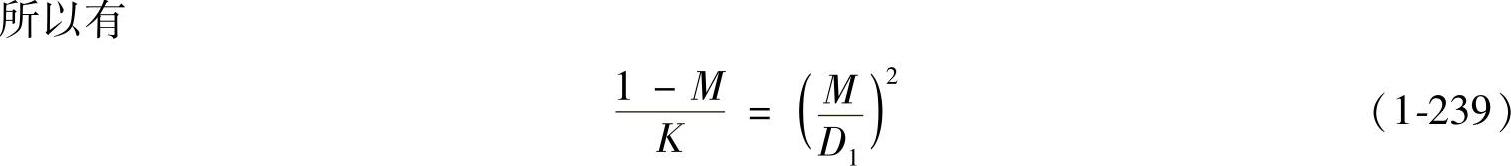
等式（1-238）可写成

式（1-240）不等式是符合实际的，因为：①开关时间远远小于输出滤波器的时间常数；②由于在CCM下的M（D₁）比在DCM下的MD₁/（D₁+D₂）小，因此可得

利用式（1-240）的不等式，还可得

这样就可得到

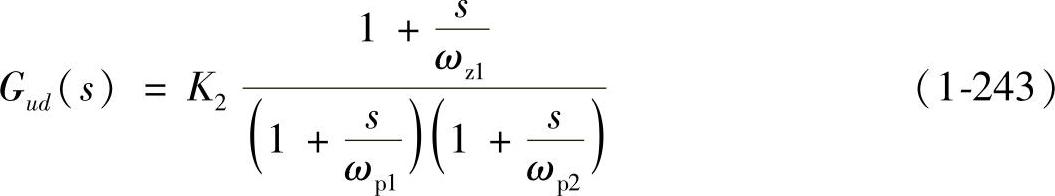
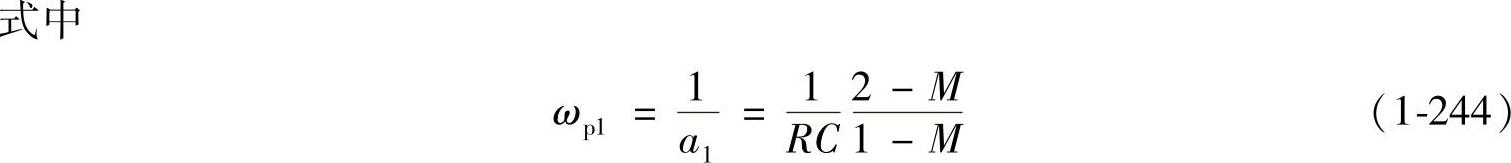
可见式（1-244）的极点是主导极点，它与用状态空间平均法建立的理想Buck变换器在DCM下的传递函数完全一致，由式（1-245）所示的第二极点可得如下不等式

当变换器工作在DCM和CCM临界时第2个极点始于f_s/π将极点向外（向后）移，则变换器进入DCM。

举例

表1-9 DCM下负载为32ΩBuck变换器电路实验数据表

Buck变换器在DCM时，控制-输出传递函数频率特性的仿真及实测曲线如图1-55所示。实验数据见表1-9。

图1-55 Buck变换器在DCM下的控制-输出传递函数频率特性曲线

a）幅频特性 b）相频特性

1—实测特性 2—仿真特性

在图1-55中，曲线1为实验测试所得的频率特性曲线，曲线2是用上面推导的非理想Buck变换器DCM模型在Mathcad软件上仿真得到的频率特性曲线，由此可见，所推导的模型接近实际模型。