如图1-32所示为已建立的非理想Buck变换器在CCM下的交流小信号等效电路。为了进一步定量分析非理想Buck变换器的低频动态特性，可根据图1-32来建立非理想Buck变换器的交流小信号s域等效电路模型，如图1-33所示。

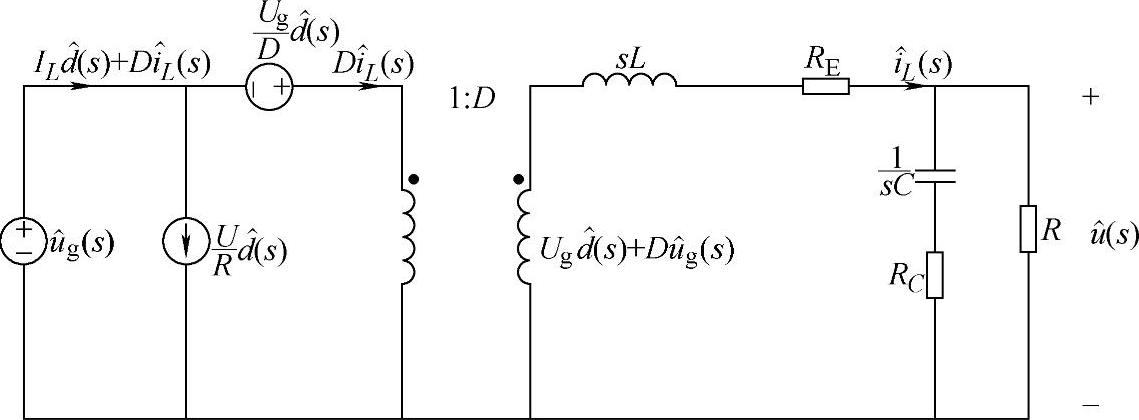
图1-33 非理想Buck变换器在CCM下交流小信号s域等效电路

根据图1-33可以导出非理想Buck变换器在CCM下的传递函数（设暂不考虑滤波电容的等效电感L_C，否则传递函数为三阶）。

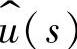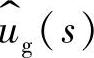1.输出电压对输入电压的传递函数

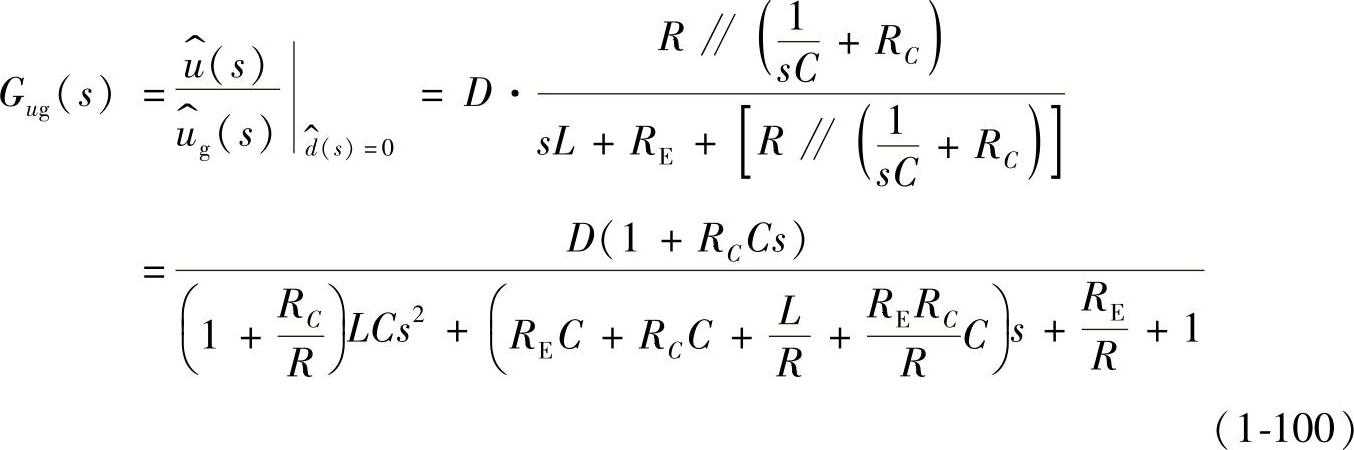
式（1-100）是二阶系统，可化简为标准二阶系统，则有

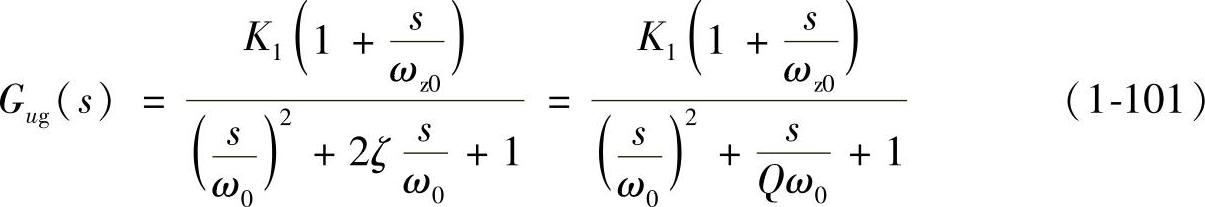
将式（1-100）与式（1-101）右边各项对应后，则有

放大倍数：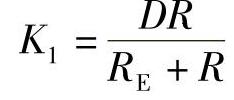

转角频率：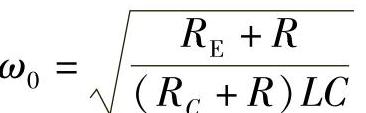

阻尼比：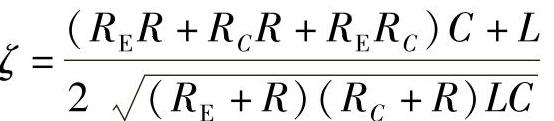

品质因数：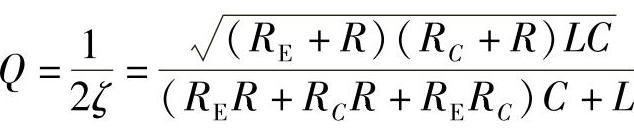

零点角频率：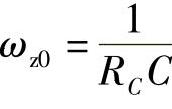

2.输出电压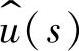对控制变量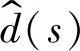的传递函数

化成标准式为

将式（1-102）和式（1-103）右边各项对应后，则有

放大倍数：

3.开环输入阻抗Z（s）

令，则

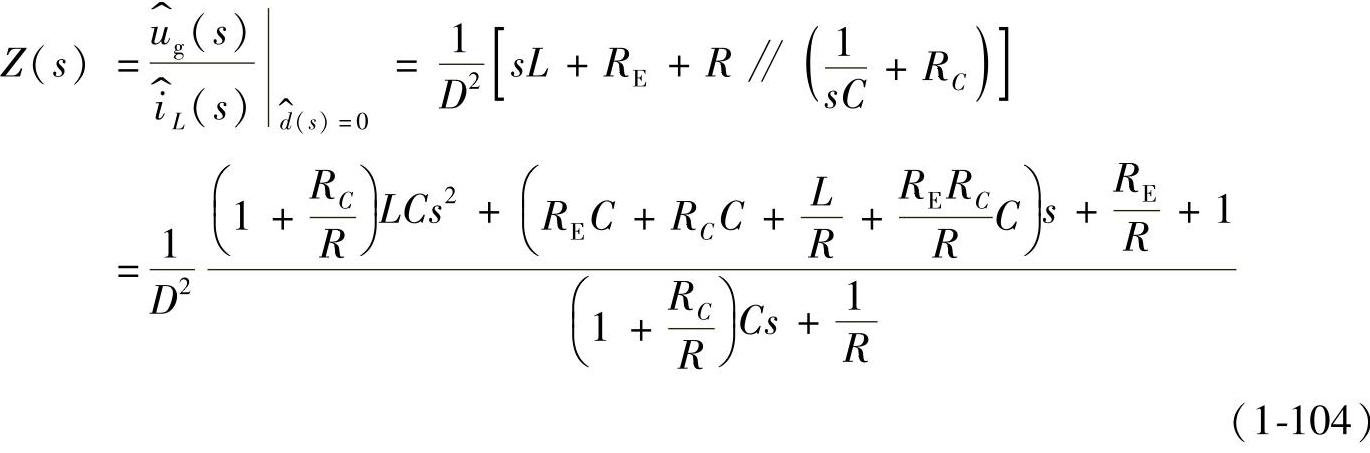
化成标准形式，则有

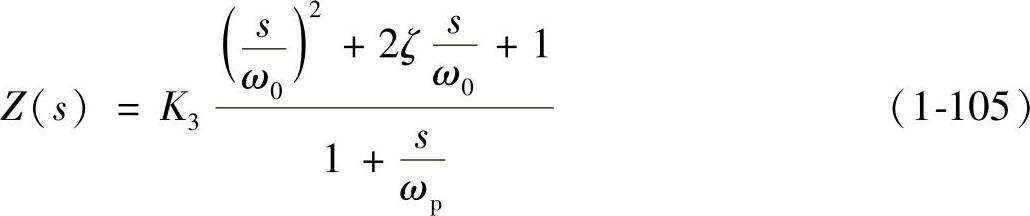
将式（1-104）和式（1-105）右边各项对应后，有

放大倍数：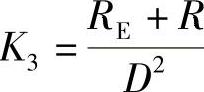

极点角频率：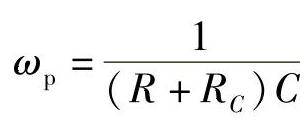

4.开环输出阻抗Z_out（s）

令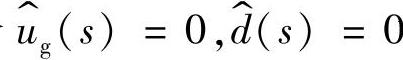，则

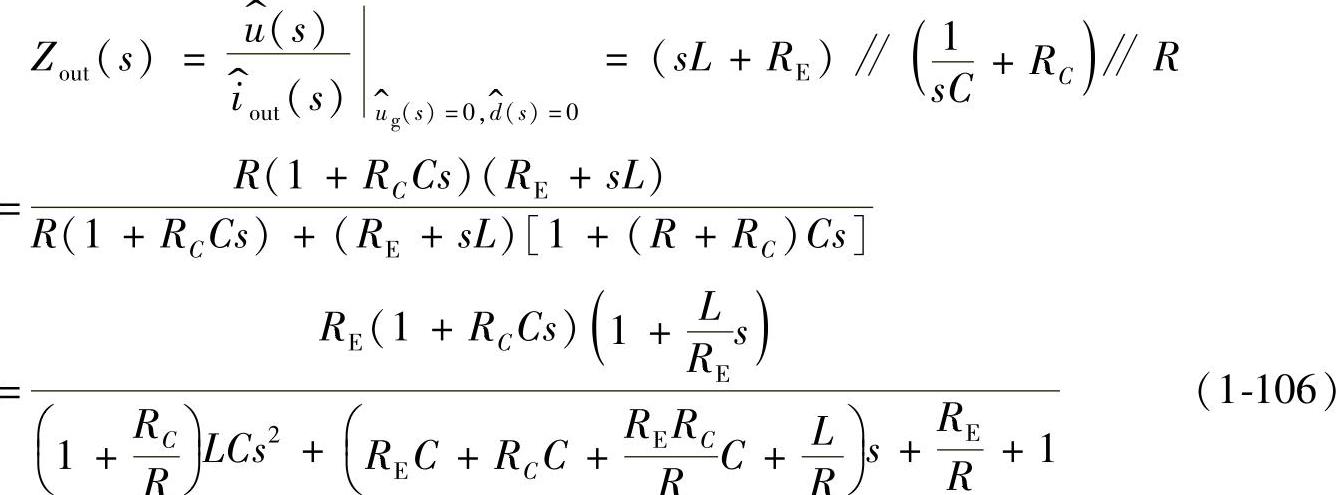
化成标准式：

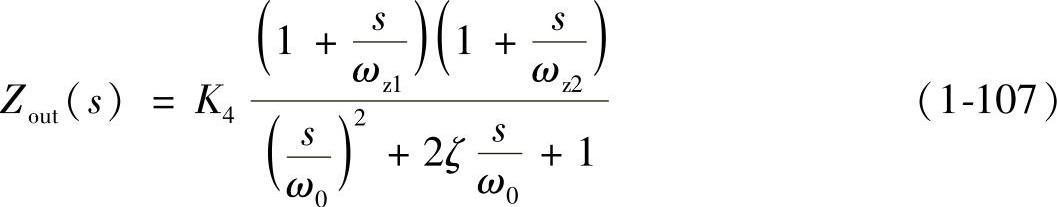
将式（1-106）和式（1-107）右边各项对应，则

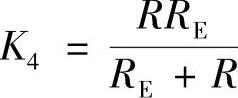
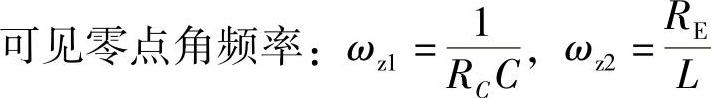
讨论：（1）当s=0时，由式（1-100）、式（1-102）、式（1-104）和式（1-106）分别推出：

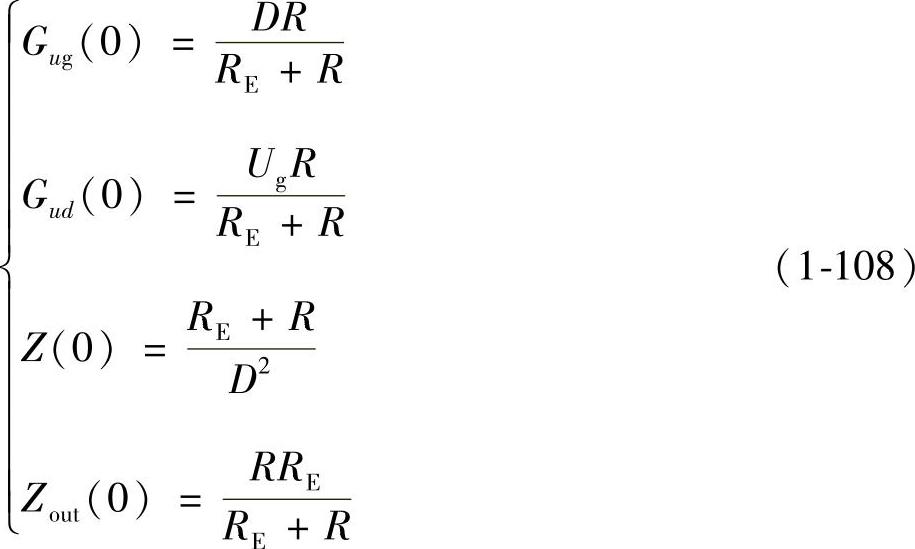(www.daowen.com)

它们分别是交流小信号特性的低频渐近线，且由式（1-108）可知这些低频渐近线均与电感支路的等效总电阻R_E大小有关；

（2）当s→∞时，由式（1-100）、式（1-102）、式（1-104）和式（1-106）分别推出：

它们分别是交流小信号特性的高频渐近线。

如果令R_on=0、U_VD=0、R_VD=0、R_L=0、R_C=0，则式（1-100）、式（1-102）、式（1-104）和式（1-106）分别为：

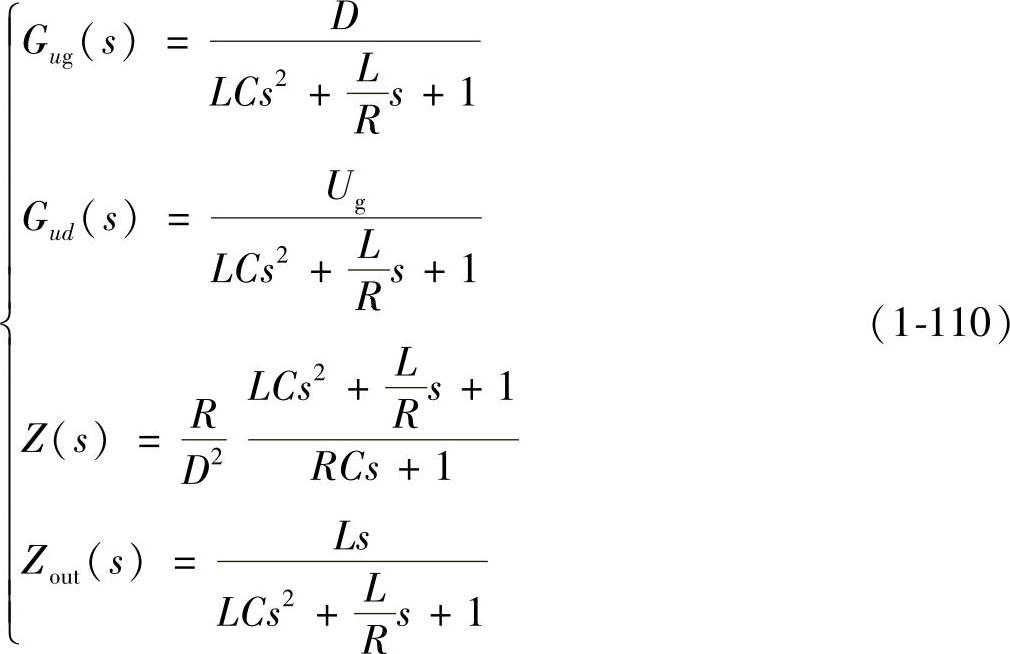
式（1-110）即为理想Buck变换器在CCM下的动态小信号特性，与用其他方法推导的结果完全一致。

举例：

表1-4 CCM下负载为5.2ΩBuck变换器电路实验数据表

根据表1-4中的参数，可以求得实际实验数据如下：

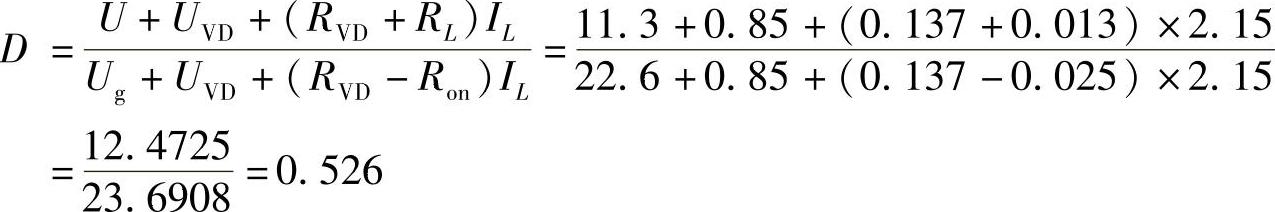
R_E=DR_on+（1-D）R_VD+R_L=0.526×0.025+（1-0.526）×0.137+0.013Ω=0.013+0.065+0.013Ω=0.091Ω

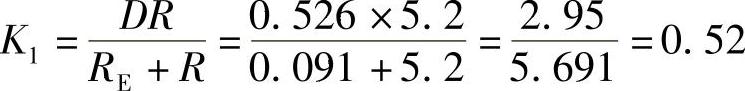
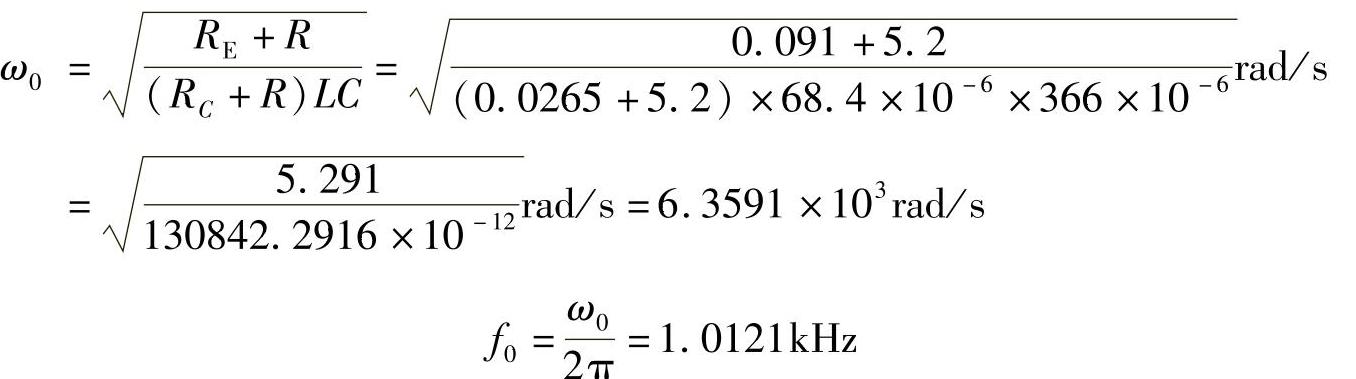
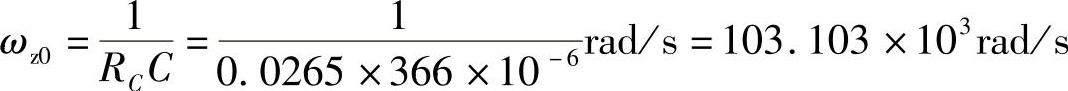
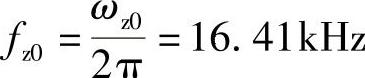
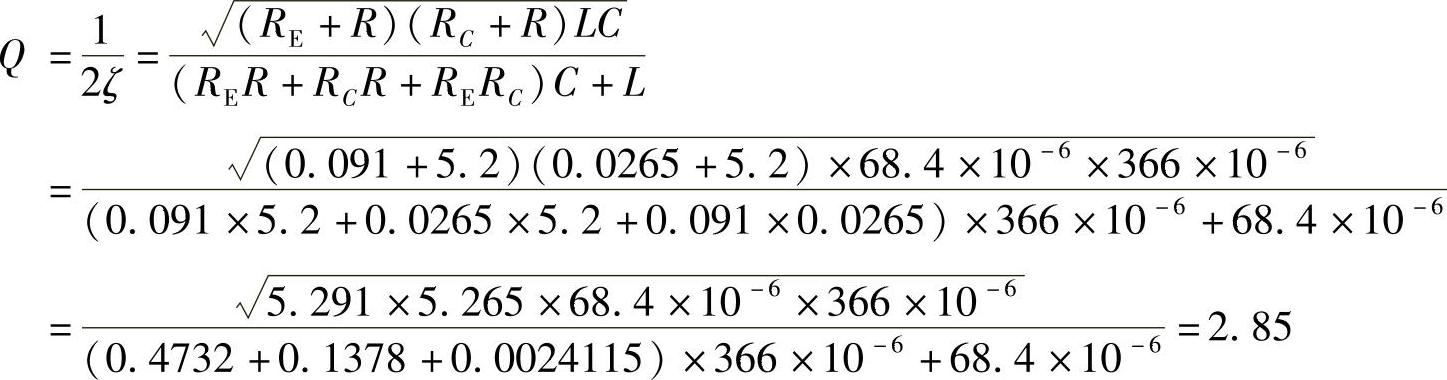
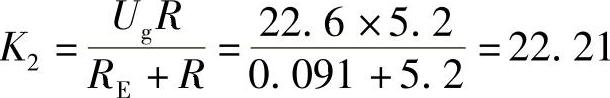
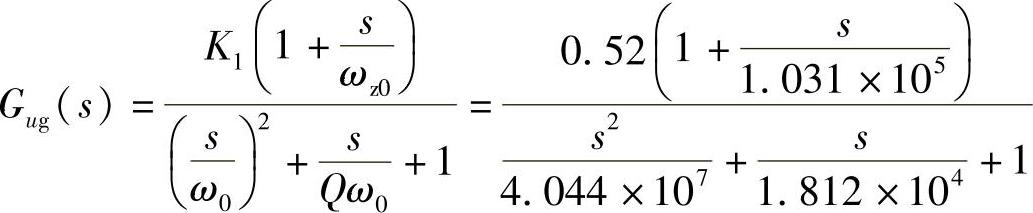
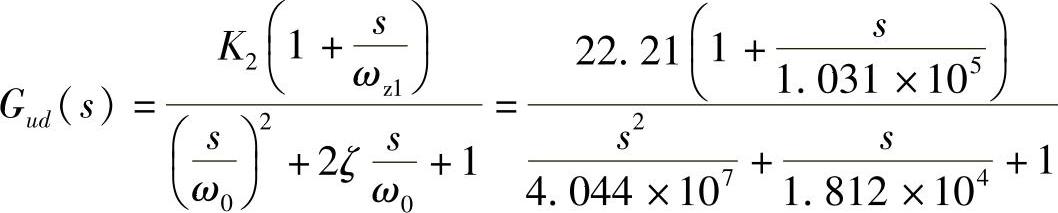
再根据表1-4中的参数，可以求得理想情况数据：

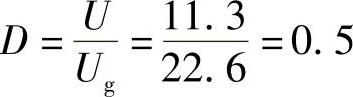
R_E=0Ω

K₁=D=0.5

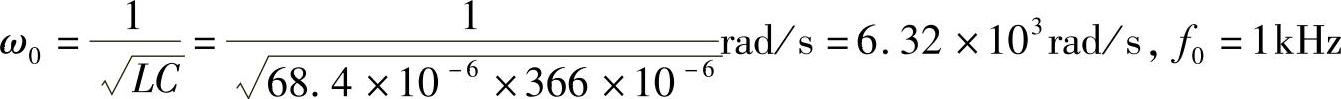
ω_z0=0

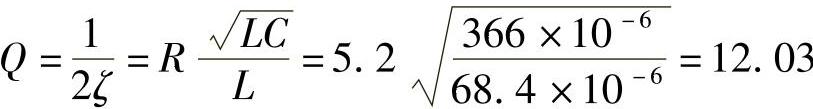
K₂=U_g=22.6

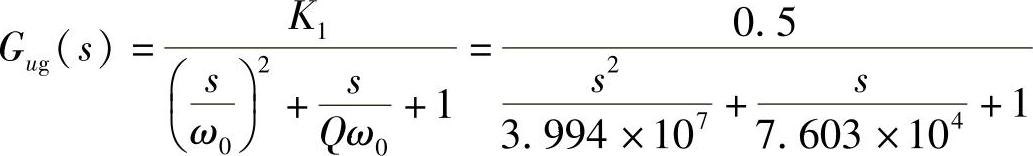
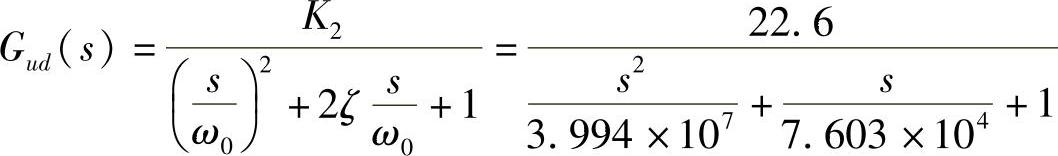
Buck变换器控制-输出频率特性如图1-34所示。图1-34a中的曲线1是非理想模型的仿真曲线；曲线2是理想模型的仿真曲线。图1-34b中的曲线是实测曲线。可见，非理想模型因考虑了变换器的寄生参数，更接近实际模型。

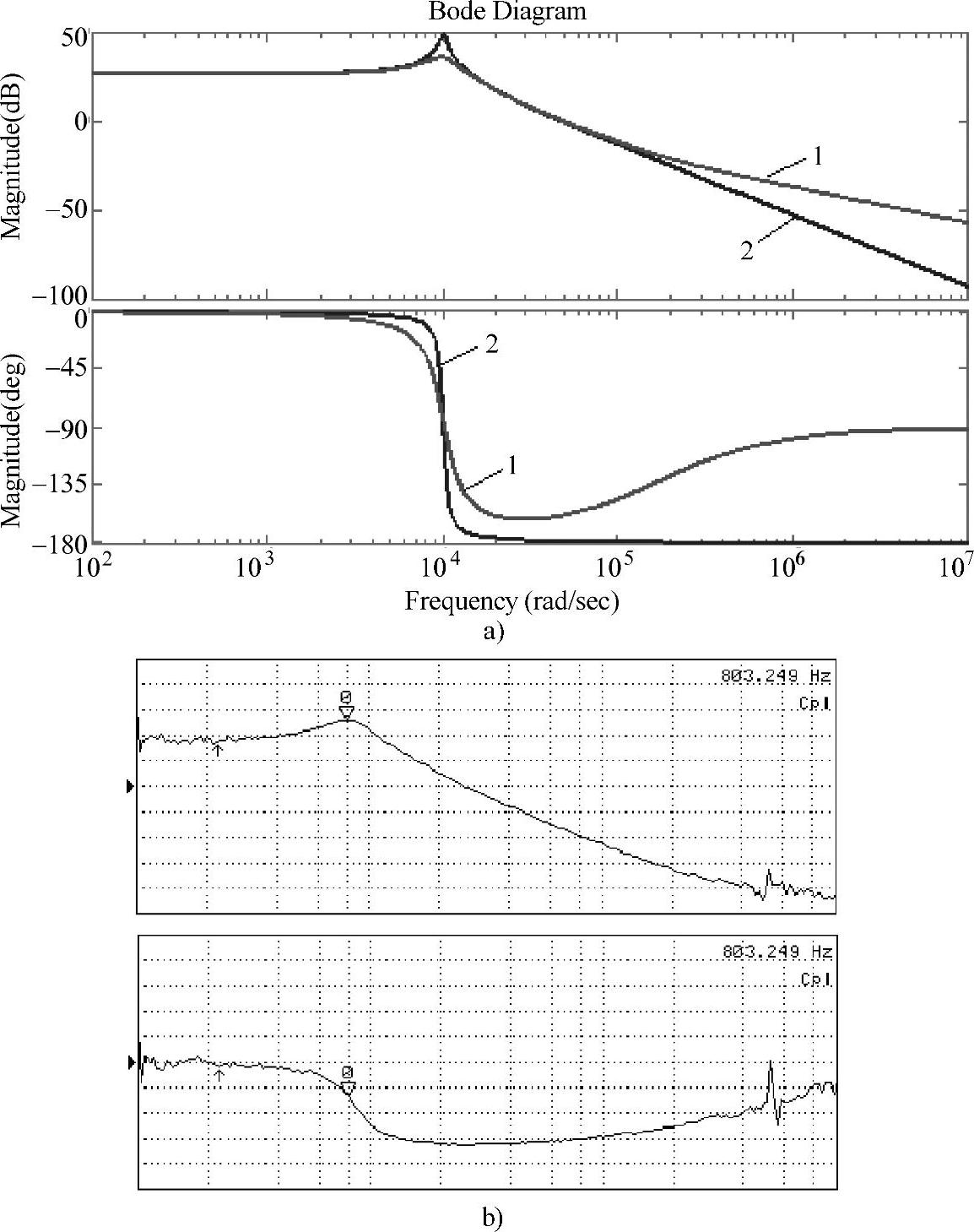
图1-34 Buck变换器控制——输出频率特性曲线

a）仿真曲线 b）实测曲线

1—精确模型仿真 2—理想模型仿真