DC-DC变换器的交流模型优化

参考文献[2]对DC-DC变换器建模方法作了详细的分类和介绍，各种常用的DC-DC变换器的交流小信号分析在相关的文献中有所介绍，这里介绍采用状态空间平均法进行DC-DC变换器的建模。

由于DC-DC变换器中存在功率开关管和二极管等非线性器件，系统属于非线性系统，但当变换器运行于某一稳态工作点附近，各电路状态变量的小信号扰动量之间的关系呈线性特性。所以，虽然DC-DC变换器为非线性电路，但在研究某一稳态工作点附近的动态特性时，仍可近似地把它当作线性系统^[4]。

Buck变换器是典型的DC-DC降压型变换器，这里以Buck变换器为例介绍状态空间平均法建模。

图1-20所示为理想Buck变换器一个开关周期的两种工作状态。

1.分段列写平均变量的状态方程和输出方程

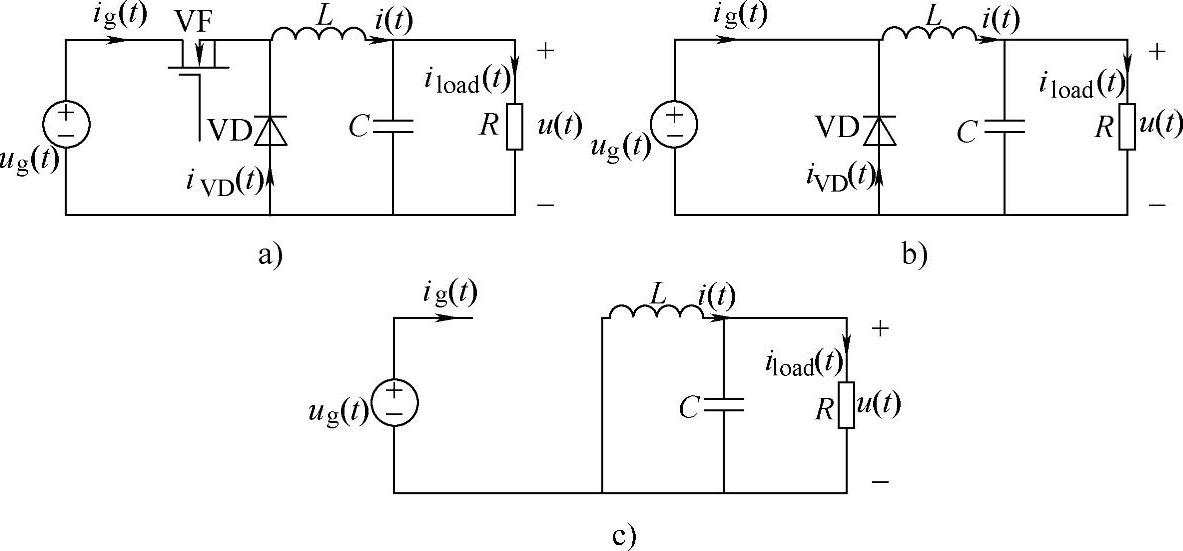
图1-20 理想Buck变换器及其两种工作状态示意图

a）理想Buck变换器 b）工作状态1 c）工作状态2

取电感电流i（t）和电容电压u_C（t）（u_C（t）=u（t））作为状态变量，组成二维状态向量x（t）=[i（t），u（t）]T；取输入电压u_g（t）作为输入变量，组成一维输入向量u（t）=[u_g（t）]；取电压源u_g（t）的输出电流i_g（t）和变换器的输出电压u（t）作为输出变量，组成二维输出向量y（t）=[i_g（t），u（t）]^T。

工作状态1：理想Buck变换器在连续导电模式下，在每一开关周期的（0，dT_s）时间内，VF导通VD截止，其等效电路如图1-20b所示。电感上的电压u_L（t）与电容中的电流i_C（t）分别为

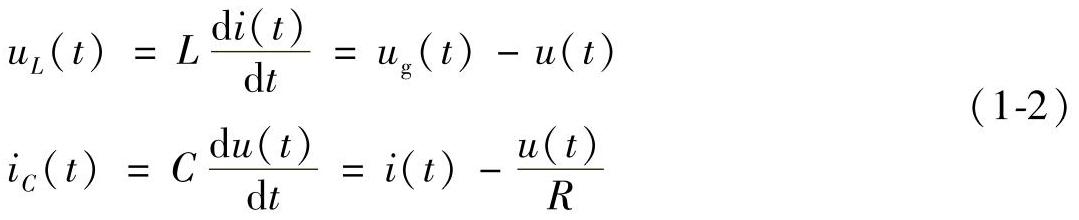
此时，输入电流i_g（t）就是电感电流i（t），输出电压u（t）就是电容电压u_C（t），则有

用状态方程与输出方程的形式表示式（1-2）和式（1-3），则有

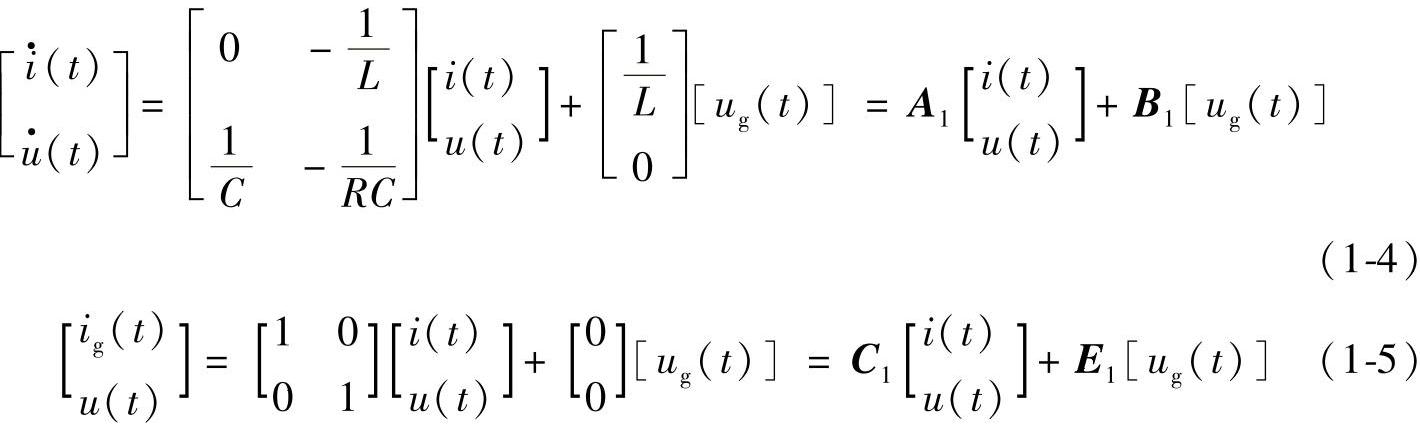
与式（1-4）、式（1-5）相对应的系数矩阵分别为

工作状态2：理想Buck变换器在每一开关周期的（dT_s，T_s）时间段内，VF截止VD导通，等效电路如图1-20c所示。电感上的电压u_L（t）和电容中的电流i_C（t）分别为

由于VF截止，输入电流i_g（t）为零，而输出电压u（t）就是电容端电压u_C（t），则有

用状态方程与输出方程的形式表示式（1-7）和式（1-8），则有

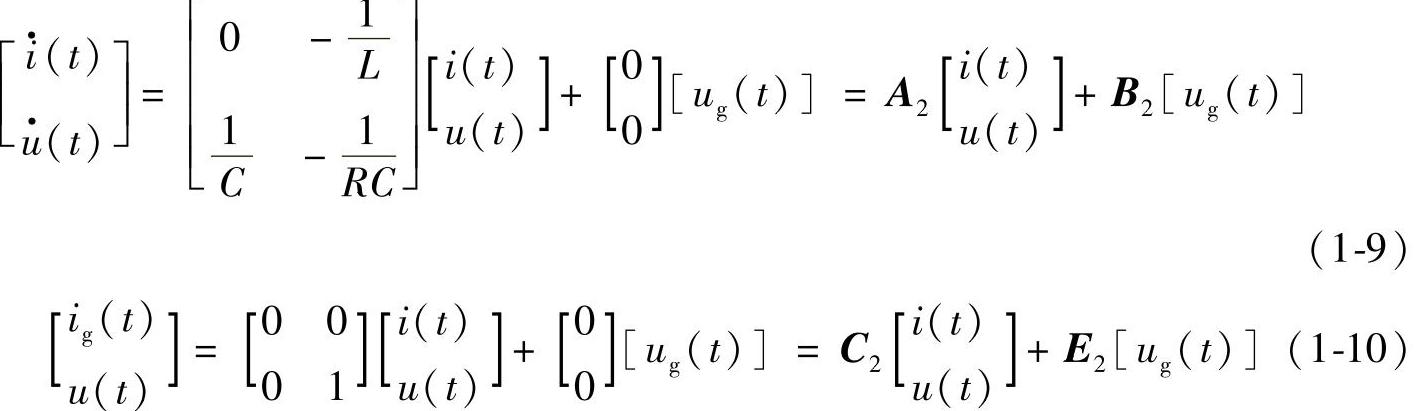
与式（1-9）、式（1-10）相对应的系数矩阵分别为

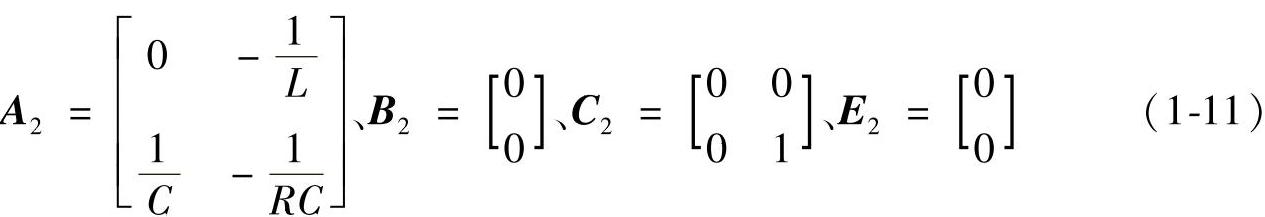
2.确定静态工作点

为了求解Buck变换器的静态工作点，需要消除变换器中各变量的高频开关纹波分量，对变量在一个开关周期内求平均值。定义状态向量的开关周期平均值为

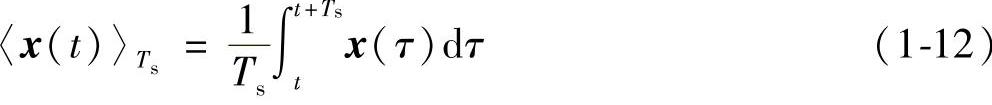
同理也可定义平均输入向量＜u（t）＞T_s与平均输出向量＜y（t）＞T_s。

求平均状态向量对时间的导数为

对式（1-13）等式右边作分段积分，并将式（1-4）和式（1-9）代入，则有

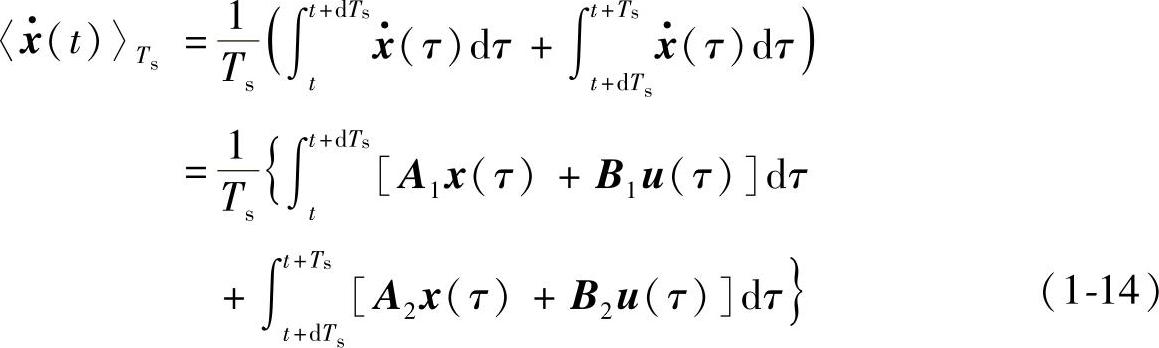
通常交流小信号的频率f_g远远小于开关频率f_s，因此在一个开关周期内求平均值可以滤除变量中的开关纹波，而不会对变量携带的其他信息（直流信息和交流小信号信息）产生太大的影响，这就是低频假设，即

f_g＜＜f_s （1-15）

不仅如此，当变换器的低通滤波器的转折频率f₀远远小于开关频率f_s时，电路中状态变量所含高频纹波分量已被大大地衰减，并远远小于直流分量与低频小信号分量之和，一般可用状态变量的平均值与瞬时值进行近似，而引起的误差可忽略，即有

＜x（t）＞T_s≈x（t） （1-16）

式（1-16）称为小纹波假设。

当变换器满足低频假设与小纹波假设时，对于状态变量与输入变量可以用其在一个开关周期内的平均值代替瞬时值，并近似认为平均值在一个开关周期内维持恒值，不会给分析引入较大的误差，即可以近似认为

且＜x（t）＞T_s与＜u（t）＞T_s在一个开关周期内可视为常量。则式（1-14）可近似化简为

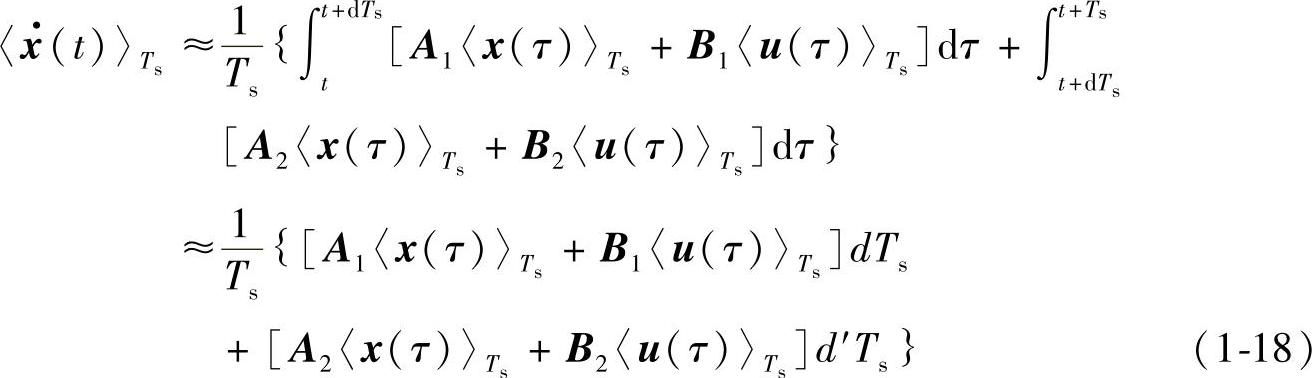
整理后得到

上式即为CCM下DC-DC变换器平均变量状态方程的一般形式。

采取相同的分析方法对输出向量求平均值，利用式（1-5）和式（1-10）可以得到一般形式的平均变量输出方程，即

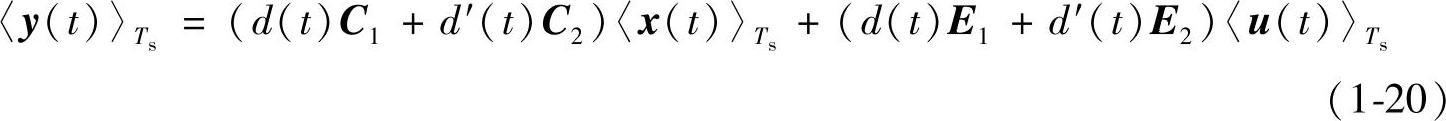
式（1-19）和式（1-20）共同组成了用平均向量表达的状态方程式的变换器解析模型。引入平均向量后，可以对变换器在一个开关周期内不同阶段的工作状态进行综合考虑，并用统一的表达式表示。

令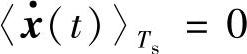，可得到变换器的静态工作点方程如下：

式中，X、U、Y分别是状态向量x（t）、输入向量u（t）与输出向量y（t）的直流分量向量，即静态工作点的向量；D为控制量d（t）的稳态值，D′=1-D。求解式（1-21）可以得到变换器状态变量与输出变量的静态工作点，即

X=-A ^-1BU （1-22）

Y=（E-CA^-1B）U （1-23）

为了求出状态变量与输出变量的静态工作点，需将式（1-6）和式（1-11）代入式（1-21）求得矩阵A、B、C、E分别为

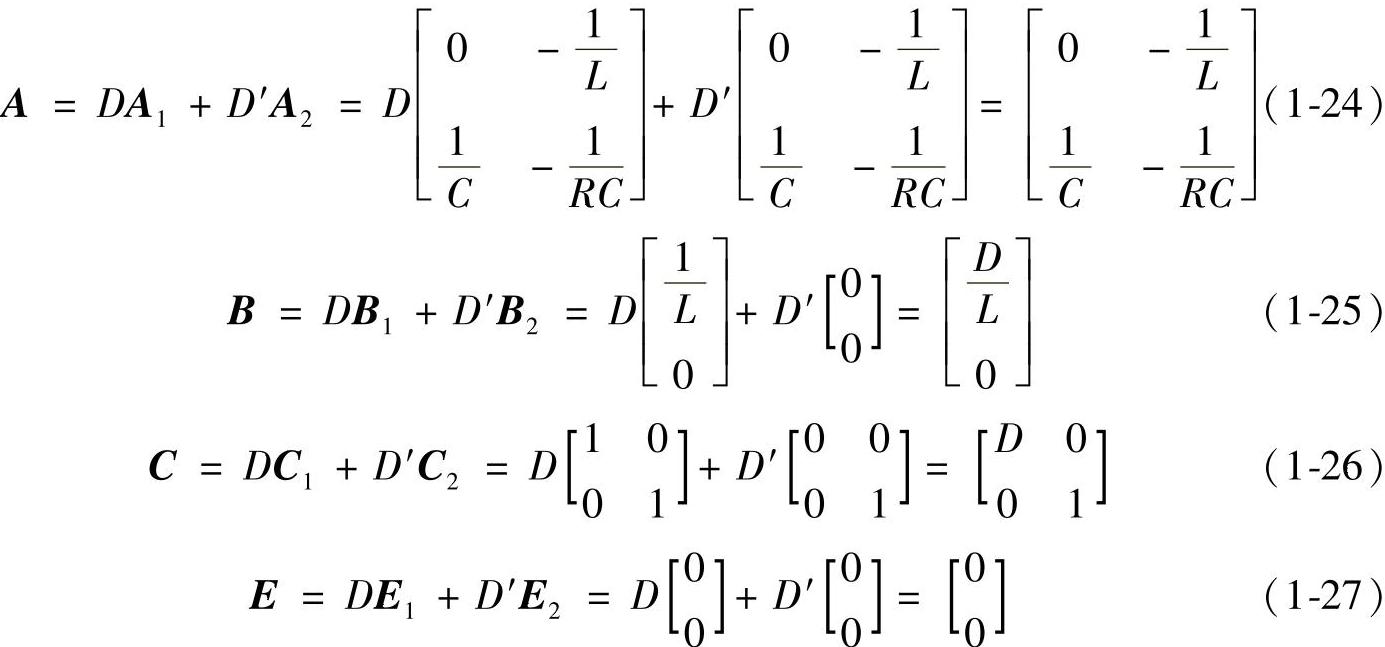
与状态向量、输入向量和输出向量相对应的直流分量向量分别为X=[I，U]^T，U=[U_g]以及Y=[I_g，U]^T。将式（1-24）～式（1-27）代入式（1-22）和式（1-23），得到理想Buck变换器的静态工作点为

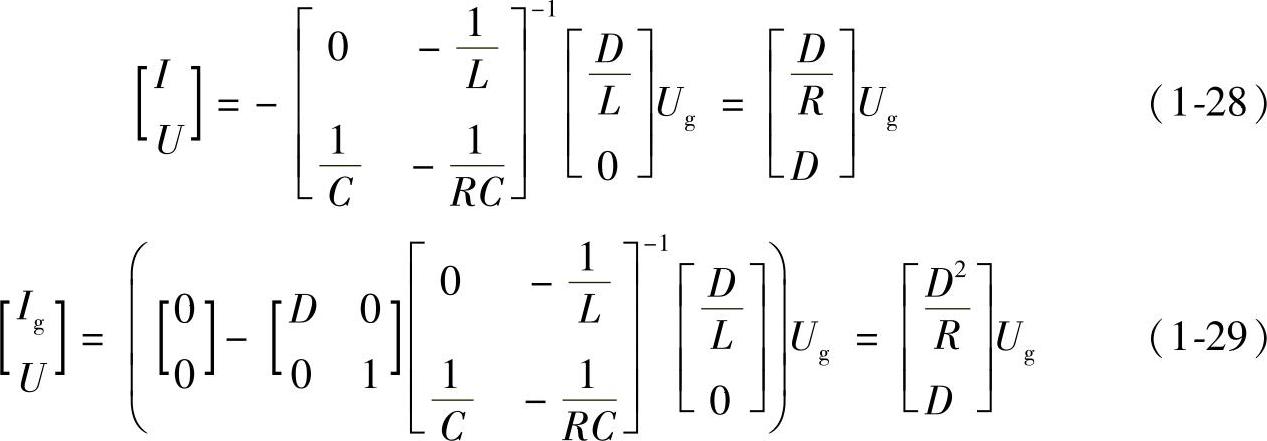
由式（1-28）得到理想Buck变换器的电压比与电感电流的稳态值，分别为

由式（1-29）得到输入电流的稳态值为

3.建立交流小信号状态方程与输出方程

上述CCM下DC-DC变换器平均变量状态方程式（1-19）和式（1-20）为非线性方程，需要用引入扰动的方法对平均变量进行分解，分解成直流分量与交流小信号分量之和。

（1）分离扰动

对平均向量＜x（t）＞_Ts、＜u（t）＞_Ts、＜y（t）＞T_s和占空比d（t）分别引入扰动，可得

式中，X、U、Y分别是与状态向量、输入向量和输出向量对应的直流分量向量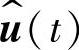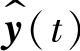；、、则分别是对应的交流小信号分量向量。

由于变换器满足小信号假设，即各变量的交流小信号分量的幅值均远远小于对应的直流分量，可将式（1-33）代入式（1-19）和式（1-20），得到

合并同类项后有

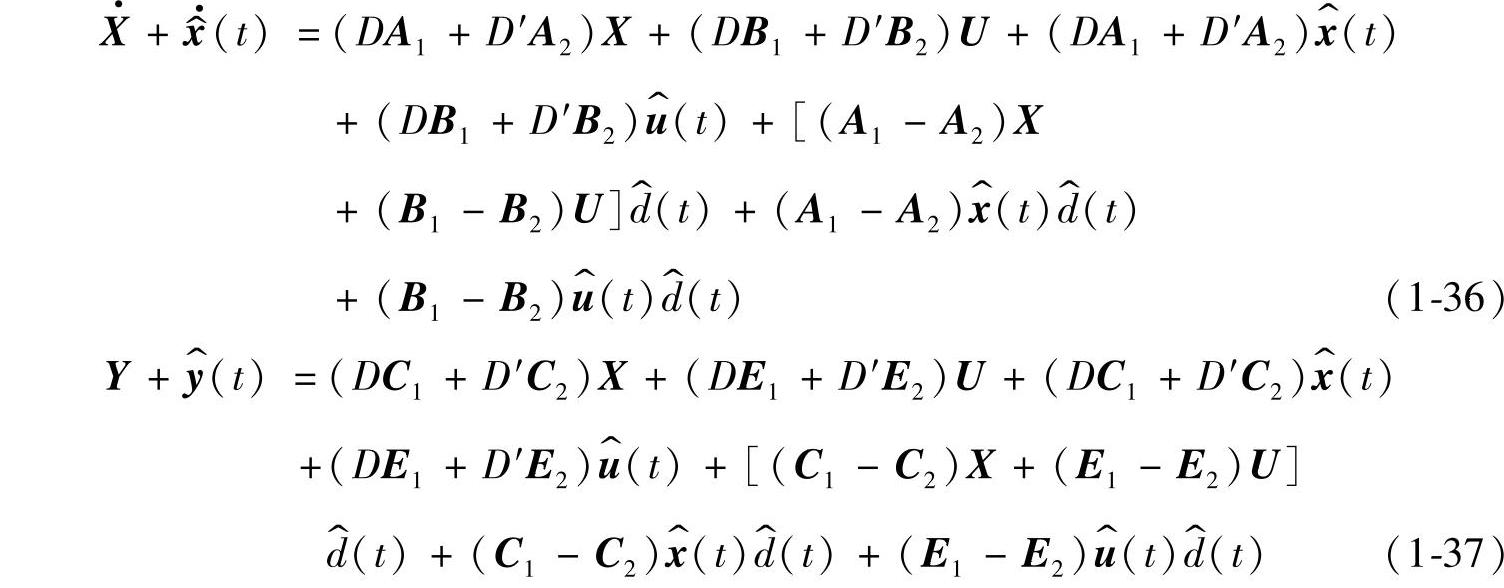
结合式（1-24）～式（1-27）整理化简后得到

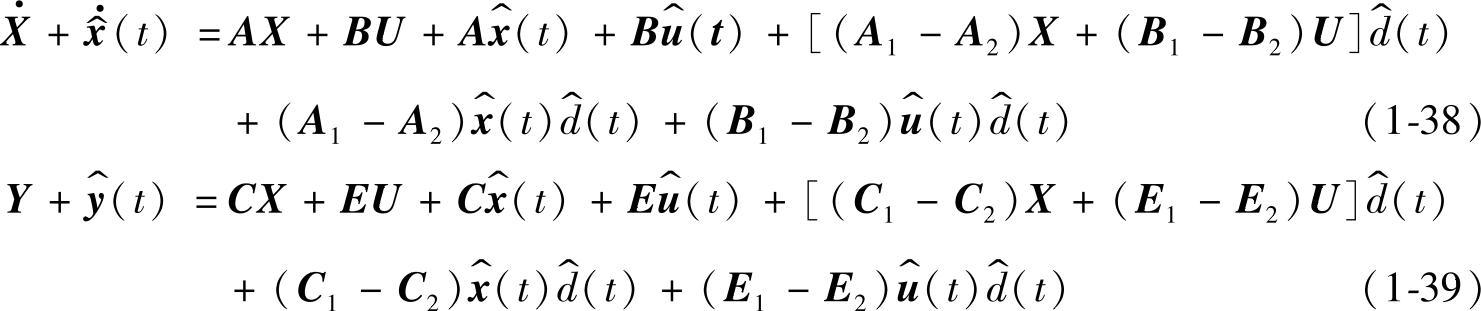
在式（1-38）和式（1-39）中，等号两边的直流量与交流量必然对应相等。令直流量对应相等，则可得到

稳态时状态向量的直流分量X为常数，则有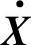=0，由式（1-40）可以解得变换器的静态工作点，即可得到式（1-22）和式（1-23）。

令式（1-38）和式（1-39）中对应的交流项相等，可得

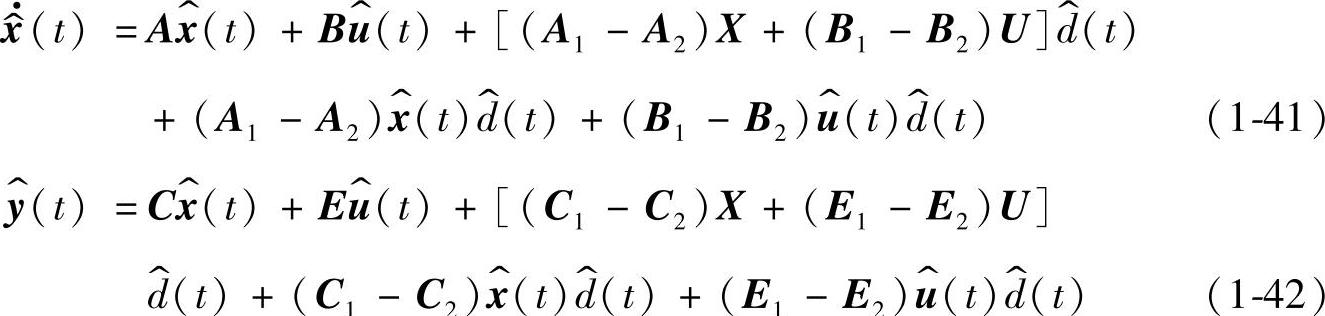
式（1-41）和式（1-42）分别为变换器的交流小信号状态方程与输出方程，方程中状态向量X的稳态值由式（1-22）确定。

（2）线性化

由于式（1-41）和式（1-42）为非线性方程，需在静态工作点附近将其线性化，式中等号右侧的非线性项均为小信号的乘积项。通常，当变换器满足小信号假设时，小信号乘积项的幅值必远远小于等号右侧其余各项的幅值，可将小信号乘积项忽略，而不会给分析引入较大的误差，达到将非线性的小信号方程线性化的目的。

对式（1-41）和式（1-42）作线性化处理，即分别从式（1-41）和（1-42）中忽略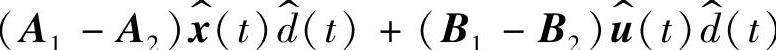和两项，可得到线性化后的小信号状态方程与输出方程，其表达式为

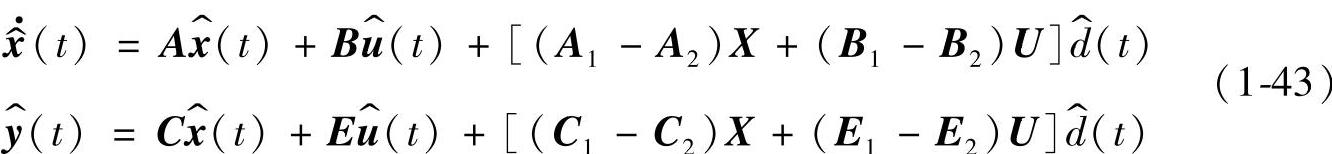
式（1-43）即是用状态空间平均法为CCM下DC-DC变换器建立的交流小信号解析模型。

若将各项矩阵A₁、A₂、A、B₁、B₂、B、C₁、C₂、C、E₁、E2、E代入式（1-43）可以得到理想Buck变换器的小信号状态方程与输出方程为

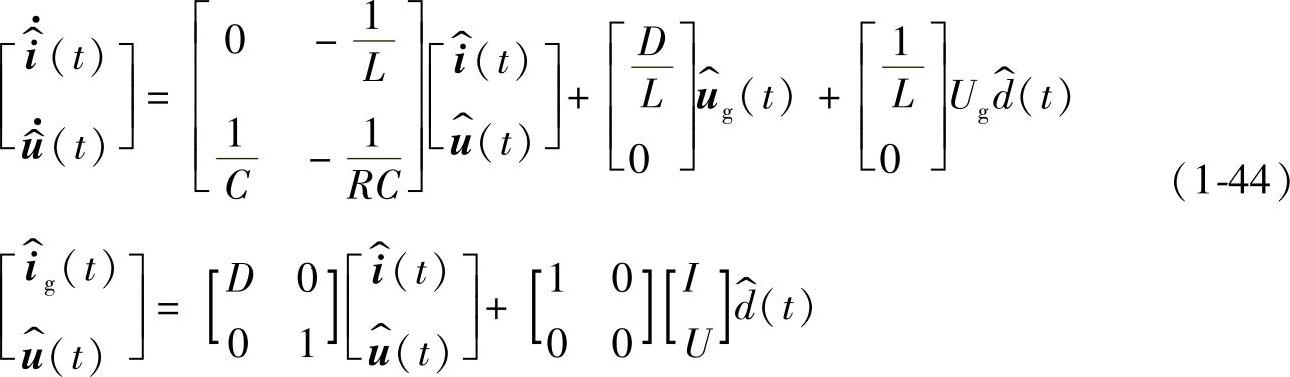
式中，直流量U和I分别由式（1-30）和式（1-31）确定。

4.小信号等效电路

根据交流小信号的解析式（1-44），可建立更为直观的交流小信号等效电路，以便分析变换器的小信号特性。

将式（1-44）改写成标量形式的状态方程，则有(https://www.daowen.com)

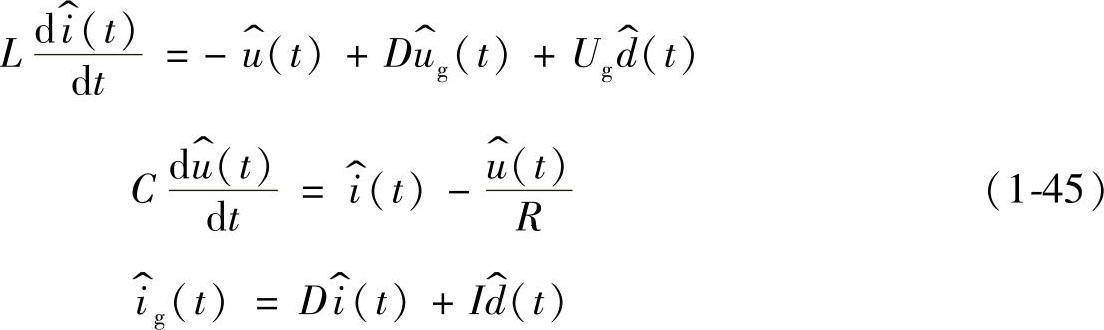
根据式（1-45）可画出Buck变换器的小信号等效电路，如图1-21所示。

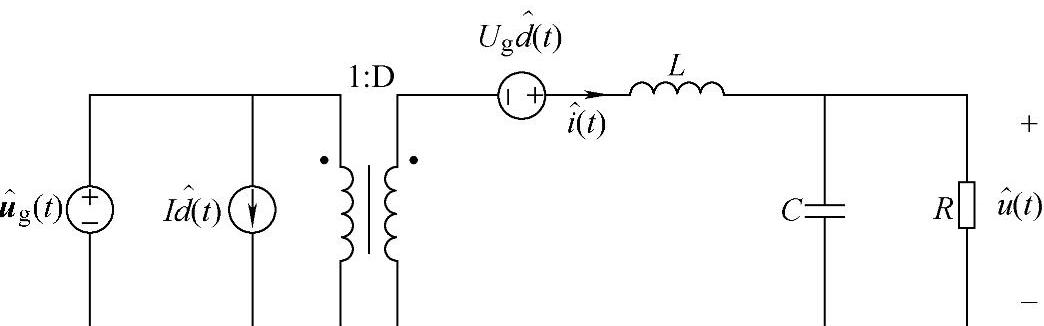
图1-21 Buck变换器小信号等效电路

5.小信号等效电路的分析

在建立了式（1-43）所示的小信号状态方程与输出方程以后，可以据此求得变换器的各种动态小信号特性。

可根据式（1-43）求解状态变量与输出变量。设各状态变量的初始值均为零，对式（1-43）作拉氏变换，得到

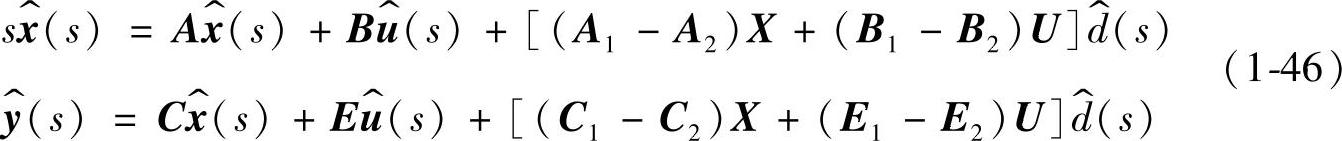
由式（1-46）可解得

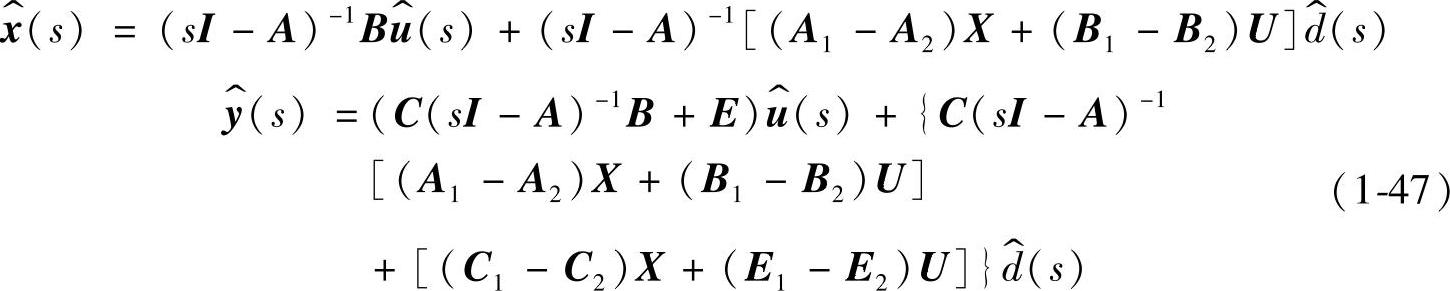
式中，I为单位矩阵。

若对式（1-47）作拉氏反变换，即可求得变换器的时域状态变量与输出变量。根据式（1-47）可以得到变换器的各传递函数，一般变换器的输入变量为输入电压u_g（t），则有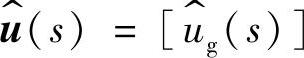，代入式（1-47）可得到以下各传递函数：

1）状态变量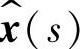对输入变量的传递函数G_xg（s）

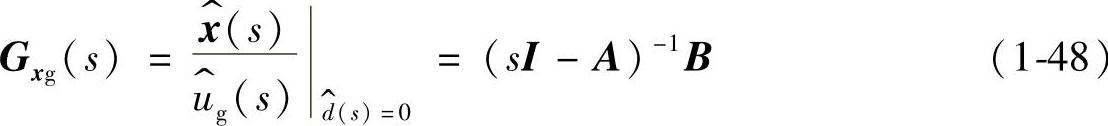
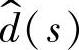2）状态变量对控制变量的传递函数G_xd（s）

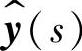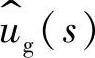3）输出变量对输入变量的传递函数G_yg（s）

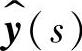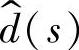4）输出变量对控制变量的传递函数G_yd（s）

用上述求传递函数的方法求解理想Buck变换器的交流小信号动态特性，得如下传递函数：

由式（1-52）可整理出理想Buck变换器输出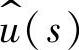对输入的传递函数G_ug（s）为

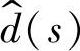若将理想Buck变换器的有关参数代入式（1-49），可得到输出对控制变量的传递函数G_ud（s）为

根据式（1-50）可得到理想Buck变换器的开环输入导纳Y（s）为

取式（1-55）的倒数则得到开环输入阻抗Z（s）为

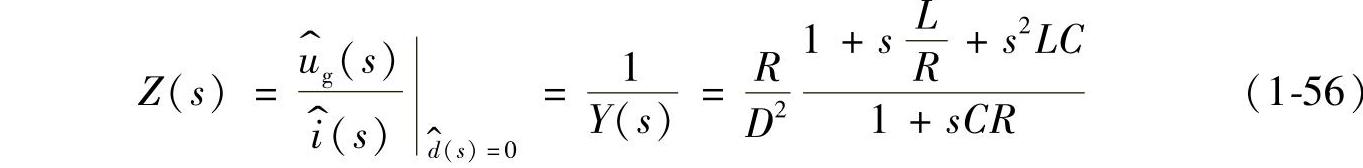
6.标准电路模型

各种变换器具有不同的结构与参数，但学者们研究表明，基本DC-DC变换器的小信号交流模型可统一成标准形式，并能直观地反映变换器的直流电压变换作用、小信号在变换器中的传递过程以及变换器的低频特性，这种标准形式被称为标准电路模型，如图1-22所示。标准电路模型具有以下作用：①直流变换作用，理想变压器可变换直流和交流小信号；②低通滤波作用，用于储存和转换能量的储能元件对高频开关纹波具有滤波作用，并对低频小信号的幅值与相位有影响；③控制变量的控制作用，用一个电压源和一个电流源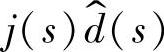模拟控制变量d（t）的小信号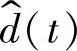的作用。

图1-22 CCM下DC-DC变换器稳态和低频小信号标准电路模型

采用图1-22所示的标准电路模型，既可模拟DC-DC变换器的直流电压变换功能，又可作为交流小信号等效电路模型，这是因为模型中电压和电流是同时用直流分量和交流小信号分量标注的。如果令标准电路模型中的所有变量和元件参数的小信号分量为零，并将电感短路、电容开路，则可模拟变换器的直流变换功能；如果令标准电路模型中的所有变量的直流分量为零，则可模拟变换器的交流动态特性。

下面以理想Buck变换器为例，为其建立标准电路模型，分析其低频动态特性。

（1）确定M（D）

先求解变换器的稳态电压比U/U_g。理想Buck变换器的稳态电压比为

（2）确定e（s）与j（s）

根据式（1-46）可知，当输入电压u_g（t）为变换器的惟一输入变量时，任意输出变量的交流小信号分量都可以表示为

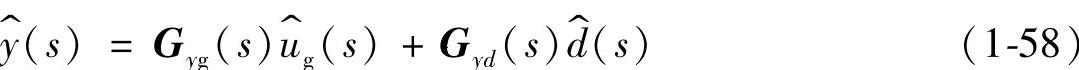
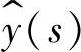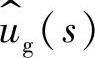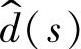式中，G_yg（s）为指定的输出变量对输入变量的传递函数；G_yd（s）为输出变量对控制变量的传递函数。

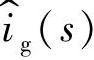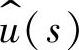若以输入电流i_g（t）和输出电压u（t）为输出变量，则利用式（1-46）可以将和表示为

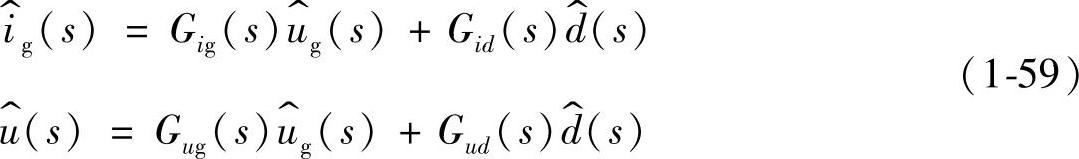
从式（1-59）中可分别整理出传递函数G_ig（s）、G_id（s）、G_ug（s）和G_ud（s）。

根据图1-22可得到

式中，Z（s）为标准电路模型的输入阻抗；H（s）为低通滤波器的传递函数，其中包括了负载电阻R的作用，如图1-22所示。因而，上述四种传递函数可表示为

由式（1-61）可得到e（s）与j（s）分别为

j（s）=G_id（s）-e（s）G_ig（s） （1-63）

以i_g（t）和u（t）为输出变量列写理想Buck变换器在两个工作阶段的状态方程和输出方程。利用上面“建立交流小信号状态方程与输出方程”小节的分析结果，将各矩阵（式（1-6）、式（1-11）和式（1-24）～式（1-27））以及状态量的稳态值（式（1-22））代入式（1-23），可得到

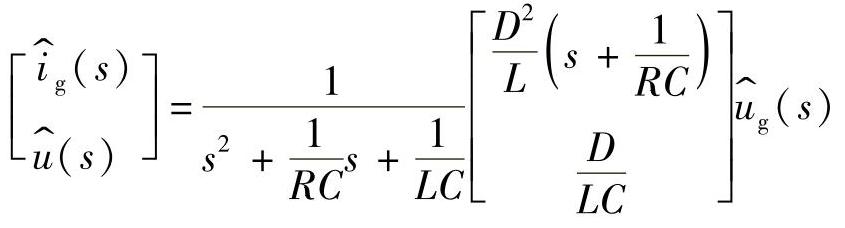
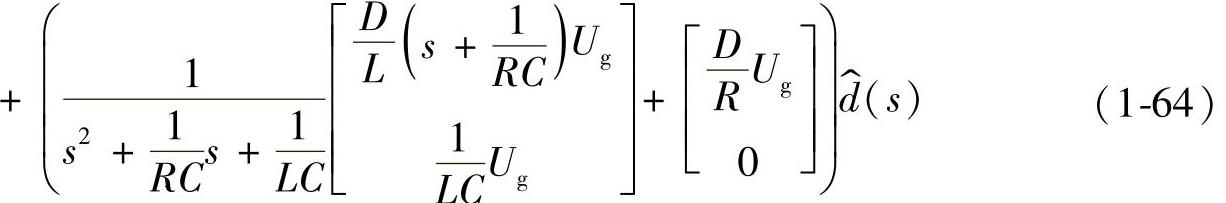
则理想Buck变换器的各种传递函数如下：

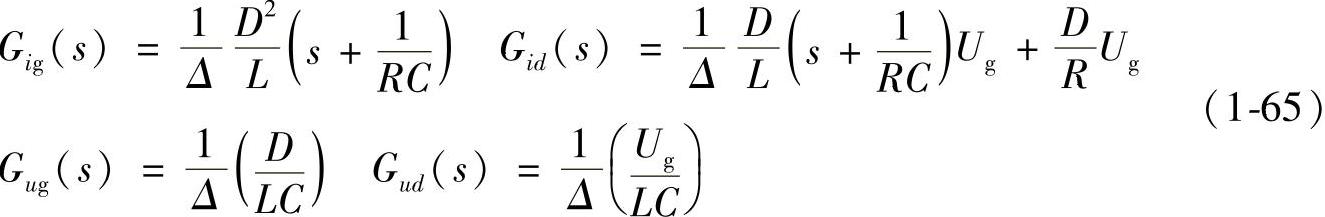
式中，Δ=s²+s/RC+1/LC。

根据式（1-62）、式（1-63）可以得到e（s）与j（s）为

（3）确定L与C

根据式（1-61）可求得H（s）

由图1-22可得

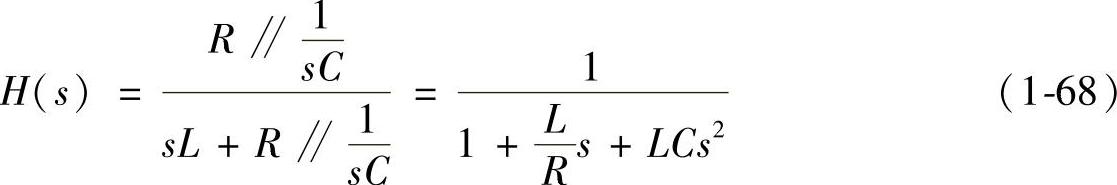
比较式（1-67）和式（1-68）可见，理想Buck变换器的标准型电路中的等效电感和等效电容值恰好与变换器中的实际电感和电容值相等。

为此，CCM下理想Buck变换器稳态和低频小信号标准型电路模型中的所有参数都已获得，将这些参数代入图1-22中，得到如图1-23所示的标准电路模型。

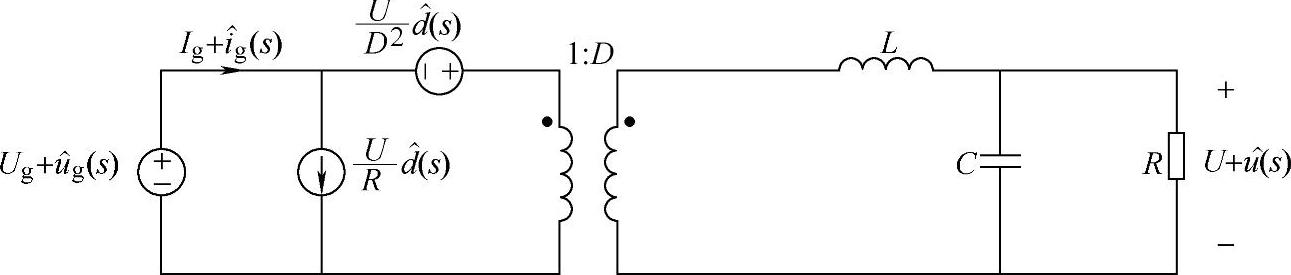
图1-23 CCM下理想Buck变换器稳态和低频小信号标准电路模型

用同样的方法也可以求得其他类型DC-DC变换器在CCM下的稳态和低频小信号标准电路模型。表1-1列出了常见的4种理想DC-DC变换器标准型电路的各项参数，将这些参数直接代入图1-22即可得到相应的标准电路模型。

表1-14 种理想DC-DC变换器CCM下标准电路模型的参数

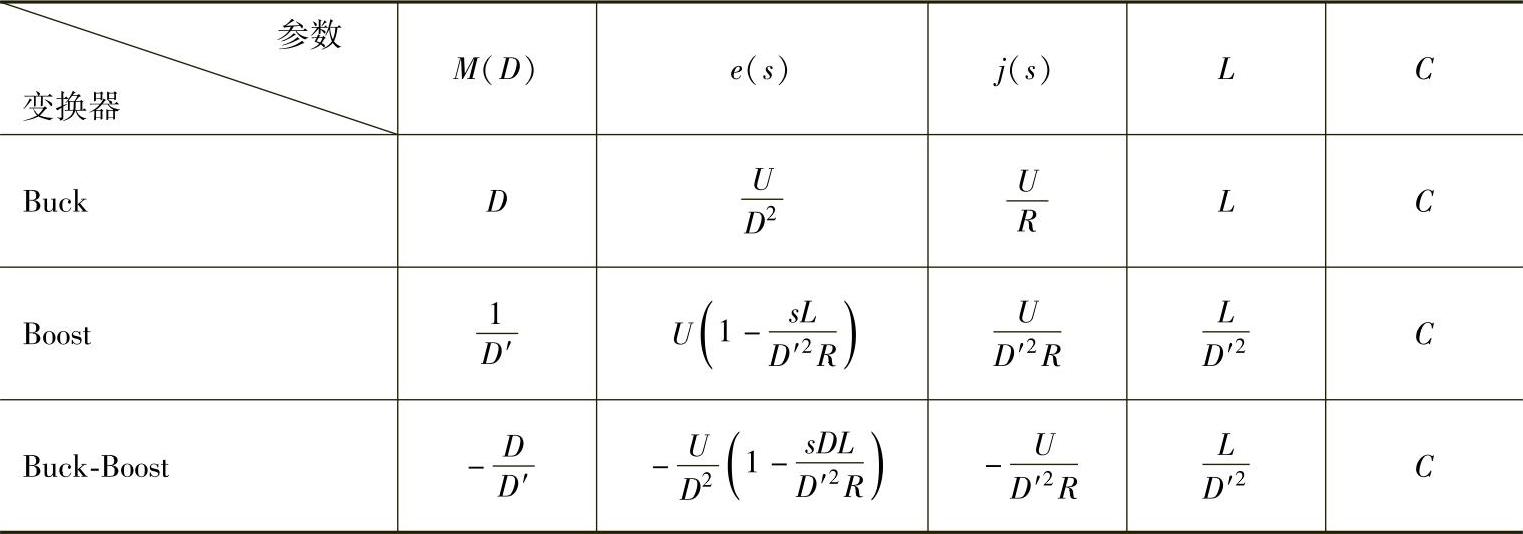
根据图1-22的标准电路模型，可以进一步分析变换器的各种动态小信号特性。以图1-23所示的理想Buck变换器标准电路模型为例，该变换器的各动态特性如下：

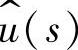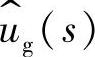1）输出对输入的传递函数G_ug（s）

2）输出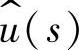对控制变量的传递函数G_ud（s）

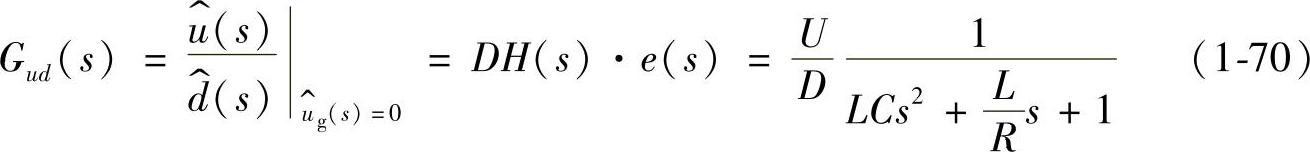
3）开环输入阻抗Z（s）

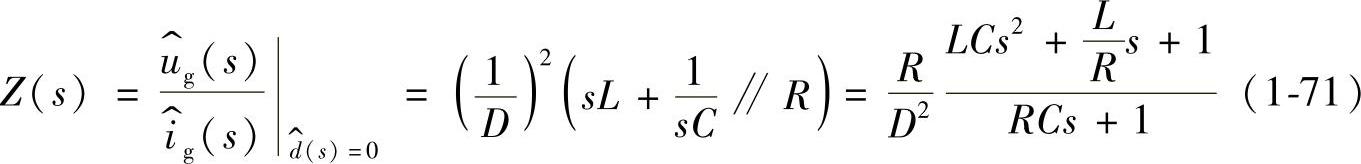
4）开环输出阻抗Z_out（s）

求开环输出阻抗的电路如图1-24所示。

为了方便读者，将理想Buck、Boost和Buck-Boost变换器在连续导电模式下稳态和动态小信号特性列于表1-2。

图1-24 求开环输出阻抗的电路

表1-24 种理想DC-DC变换器CCM下稳态与动态小信号特性