开关变换器在启动或关闭、负载突增或突减、电源电压突升或突降等工况时，系统在大信号扰动下工作，此时系统是强非线性，因此小信号分析法不再适用。开关调节系统实质上是一个处理能量变换和进行能量控制的系统。能量的突变是系统不可避免会遇到的工况，它对系统运行构成潜在的危害，处理不当会使系统不稳或损毁。能量的突变也是系统经常会遇到的工况^[1]，因此本小节对系统在大信号扰动下的瞬态特性通过仿真实验加以介绍。

1.开关变换器启动过程分析

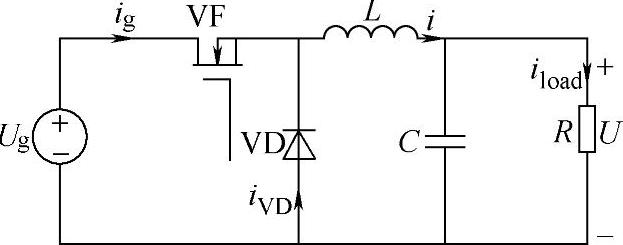
图1-1 理想Buck变换器等效电路

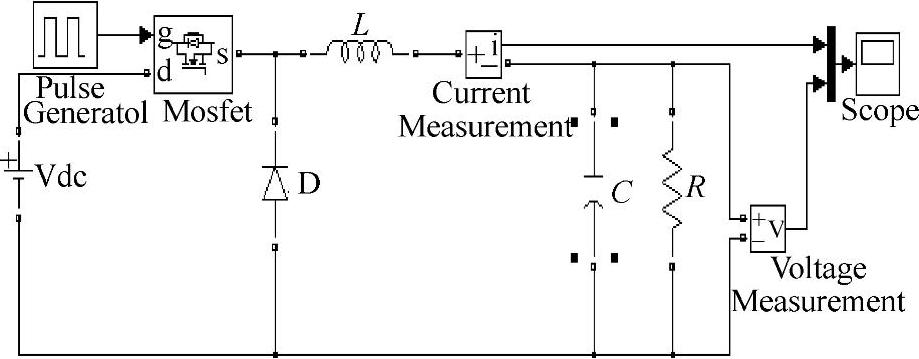
图1-2 理想Buck变换器启动时的仿真模型

Buck（降压）变换器的结构是开关变换器中最基本的拓扑结构之一，因此，以Buck变换器作为研究对象，来研究开关调节系统开环运行时的启动过程。所谓开环运行是指控制器输出的占空比D在整个启动过程中为常数，系统各储能元件的初始值为零，输入电压为单位阶跃函数，即u_g（t）=U_g×1（t）。Buck变换器理想等效电路如图1-1所示，其中MOSFET（VF）的开关周期是T_s，开通时间为t_on，占空比为D。

仿真实验的理想Buck变换器参数为：输入电压U_g=23.0V，滤波电容C=370μF；CCM下动态电感L=66.64μH，负载R=4Ω，输出电压U=11.4V。

用MATLAB仿真软件构建理想Buck变换器仿真模型如图1-2所示。图1-3所示为理想Buck变换器开环启动运行的瞬态响应曲线，曲线1为输出电压u（t）瞬态响应，曲线2为电感电流i_L（t）瞬态响应。

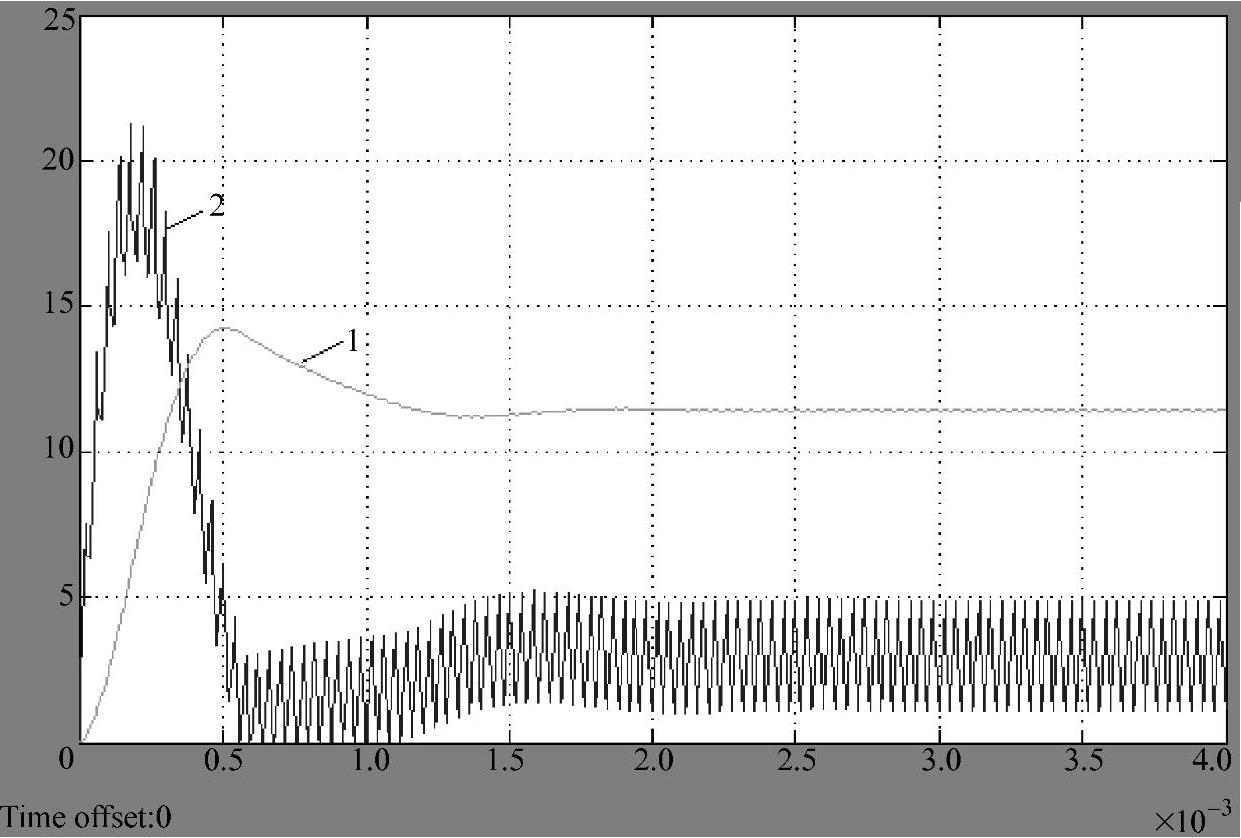
图1-3 理想Buck变换器启动响应曲线

1—输出电压 2—电感电流

仿真实验测得Buck变换器的一些主要时域指标：上升时间t_r=223.5μs，调节时间t_s=1.65ms，超调量σ=25.15%，上冲电压ΔU=2.8667V，最大峰值电压U_max=14.2667V，最大峰值电感电流i_Lmax=21.270A，稳态时的平均电感电流i_Lav=2.85A。

由理想Buck变换器启动过程的仿真实验可得到如下结论：

1）电压过高，过冲电压是稳态值的25.15%。实际中，一般要求过冲电压低于稳态值的10%，仿真结果不符合实际要求的原因在于主电路和控制电路的工作时序问题。仿真中的工作时序是控制电压已正常工作、输出的占空比为稳态的情况下，然后启动主电路，使过冲太高。而正常的工作时序应是主电路先于控制电路启动，控制电路中含有软启动电路或控制策略，使开关调节系统在满足调节时间指标的前提下，占空比从零逐渐增大，直至进入稳态。因此，采用软启动和主电路启动先于控制电路启动的措施，能减小输出电压过冲，确保系统安全启动。

2）电感电流的峰值过高，过高的峰值电流可能会使电感铁心处于饱和，严重时会烧坏主电路。实际中，可增加限流保护电路或增设电流反馈环。

如果用1.2.2节将要介绍的交流小信号分析法来分析开关变换器的启动过程，情况又将如何呢？见下面的分析和仿真实验。

按交流小信号分析法，CCM下Buck变换器开环启动过程等效电路如图1-4所示。对于同一变换器，其参数不变（同上），并设电路中的储能元件的初始值为零，输入电压为阶跃函数U_g（s）=U_g/s，则输出电压表达式为

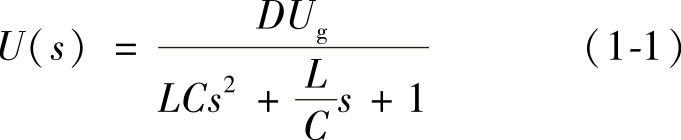
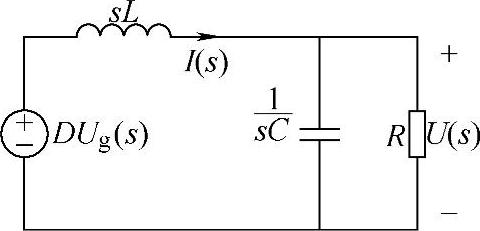
图1-4 开环启动过程的等效电路

将已知参数代入式（1-1），并用C语言编制

如下MATLAB仿真程序：

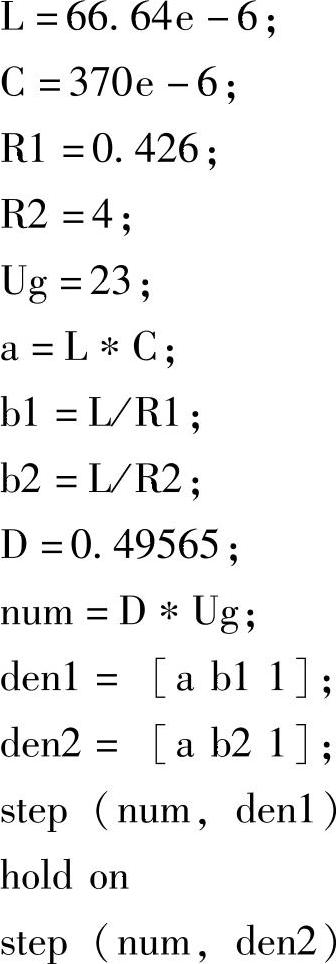
将上述程序在MATLAB环境下运行后，可得图1-5所示的启动过程中输出电压瞬态响应曲线，图中输出电压曲线1和2的负载电阻R分别为4Ω和0.426Ω。

对照图1-3和图1-5所示的输出电压曲线可以得出如下结论：

1）在Buck变换器参数相同的情况下，但由于采用不同的分析方法，得到不同的瞬态响应。第二种分析方法即小信号分析法具有局限性，这种方法没有考虑主电路开关的非线性，也没有考虑控制电路中的脉宽调制器的非线性饱和特性。因此，小信号分析结果不能预测大信号扰动下系统工作的实际特性。

2）在储能元件相同的条件下（见图1-5曲线1和2），即电感L和电容C参数一定的情况下，负载不同，则阻尼比ξ（或品质因数Q）不同，超调量也不同。在本例仿真实验中，当R=4Ω，ξ=0.053，Q=9.425，U_max=21V；当R=0.426Ω，ξ=0.5，Q=1.004，U_max=13.2V。

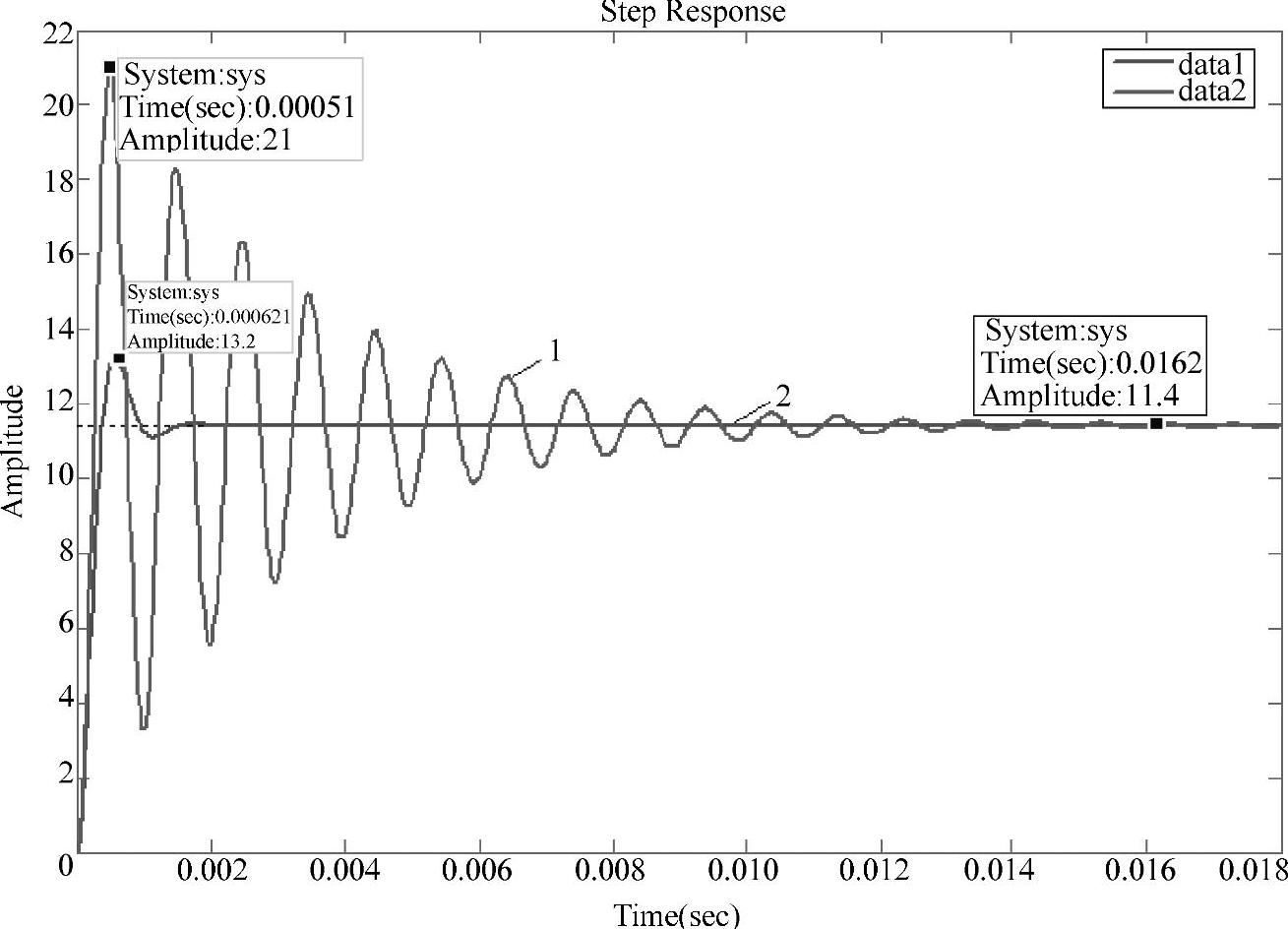
图1-5 启动过程中输出电压瞬态响应曲线

1—R=4Ω时的输出电压 2—R=0.426Ω时的输出电压

2.开关调节系统启动过程分析

在开关调节系统的动态性能指标中，输出电压在大信号条件下暂态过冲和恢复时间通常被认为是最重要的指标^[3]。在GB/T 14714—2008《微小型计算机系统设备用开关电源通用规范》中对输出电压为12V的电源指标规定如下：暂态恢复时间最大值应小于50ms，过冲幅度为+10%，电压稳定度为1.5%。下面通过仿真实验说明闭环调压系统的启动过程。

理想Buck变换器参数：输入电压U_g=23.0V，滤波电容C=370μF；CCM下动态电感L=66.64μH，负载R=4Ω，输出电压U=11.4V，采用线性反馈，反馈系数h=1，D_max=0.9，D_min=0。按电源技术指标规定的要求，本例中超调量：σ=10%；调节时间：t_s=50ms。

在MATLAB仿真环境下，闭环启动仿真模型如图1-6所示，其中闭环启动仿真模型中的采样频率为100kHz，开关频率为25kHz。输出电压和电感电流的瞬态响应曲线如图1-7所示。仿真实验测得闭环调节系统启动过程的一些主要时域指标：最大峰值电压U_max=15.12V，上冲电压ΔU=3.72V，调节时间t_s=1.5ms，超调量σ=32.63%，最大峰值电感电流i_Lmax=27.1A，稳态时的平均电感电流i_Lav=2.85A。

对照图1-3和图1-7可得到如下结论：

1）输出电压和电感电流的变化规律相同，因此可用开环开关变换器近似地估算在启动过程中变换器各量的变化规律，但定量分析中存在误差。

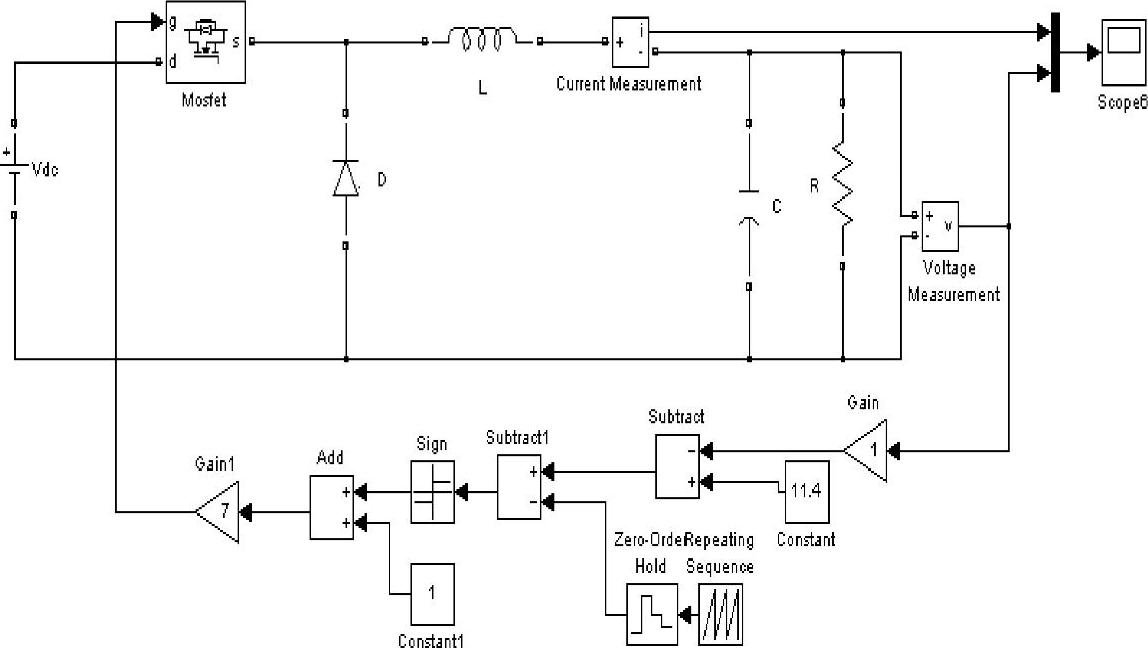
图1-6 闭环调节系统启动过程仿真模型

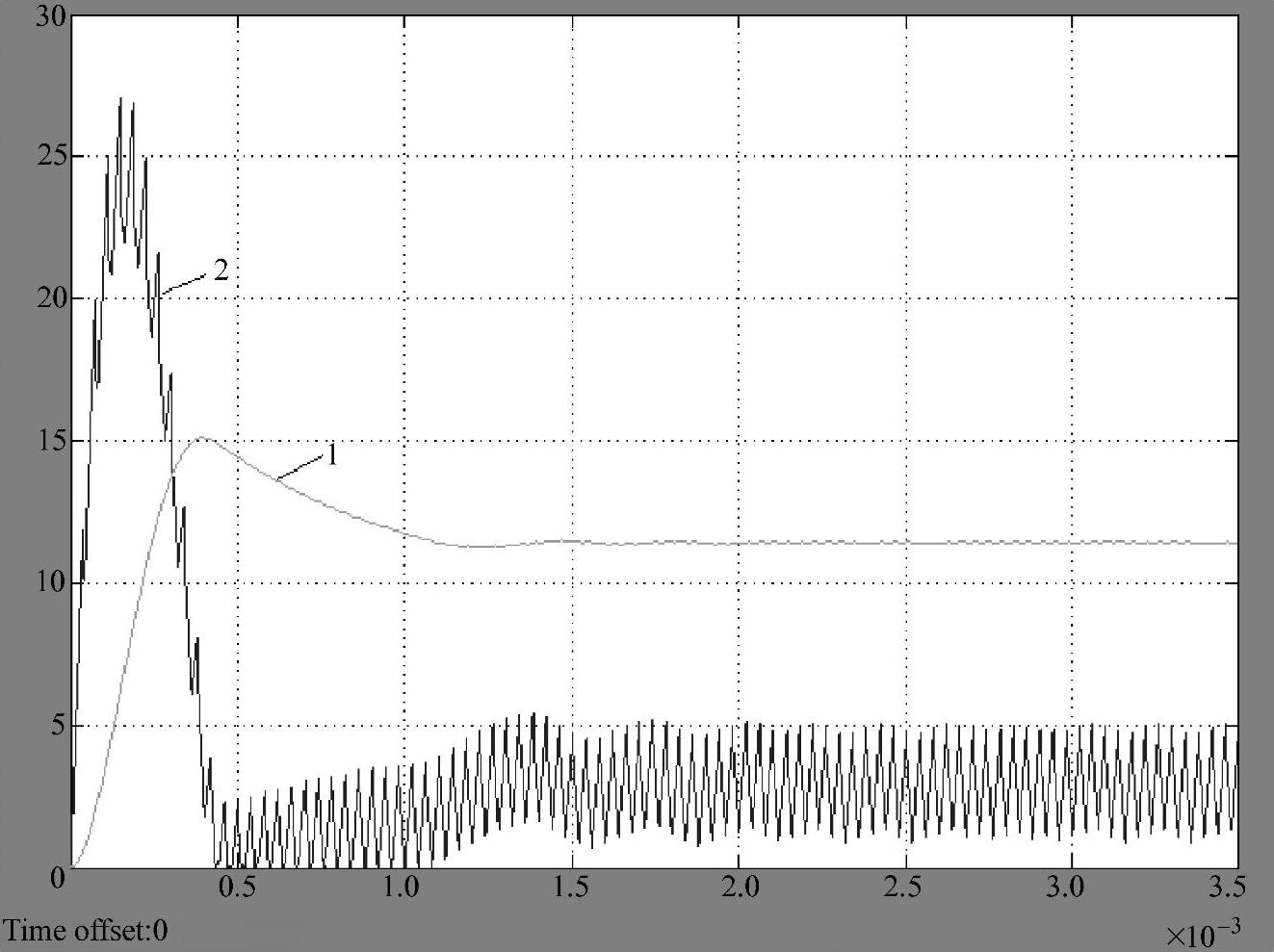
图1-7 闭环调节系统启动过程瞬态响应曲线

1—输出电压 2—电感电流

2）一般情况下，输出电压的实测值应小于计算值。其原因是采用电压反馈后，当输出电压超过给定电压值时，脉冲宽度调制器的非线性特性会使占空比在一段时间内保持在最小值D_min，限制输出电压的上冲幅值。

3）电感电流的实测值远远大于计算值。启动过程的瞬态响应表明，电感电流峰值超前输出电压峰值，在输出电压达到稳态值之前，电感电流单调上升并已超过了稳态值。原因在于当输出电压远小于给定值时，脉宽调制器的非线性特性会使占空比在启动初始时间内保持在最大值D_max，系统处于失控状态，又由于D_max大于稳态占空比D，使电感电流产生过大的上冲幅值。要想限制电感电流的上冲幅值，可采用电流反馈方法。

3.开关调节系统负载突变的过渡过程分析

为了研究开关调节系统加载或卸载时变换器的工作过程，对同一个Buck变换器开关调节系统，保持输入电压恒定，使负载电阻突增或突减，相应的输出电流突降或突增，仿真其输出电压的瞬态响应。

仿真实验1：输出电流的初始值I₁=5.8A，突降到I₂=1.8A，即负载电阻由R′=R∥R₁突变到R（R′＜R）。突卸负载时的仿真模型如图1-8所示，系统启动以后达到稳态（约2ms），设置理想开关（Ideal Switch）在初始时闭合，而在卸载瞬间（4ms处）断开。卸载瞬间的瞬态响应曲线如图1-9所示，图中曲线1为输出电压瞬态响应，曲线2为电感电流瞬态响应，可见卸载瞬间输出电压上冲，而电感电流下降。

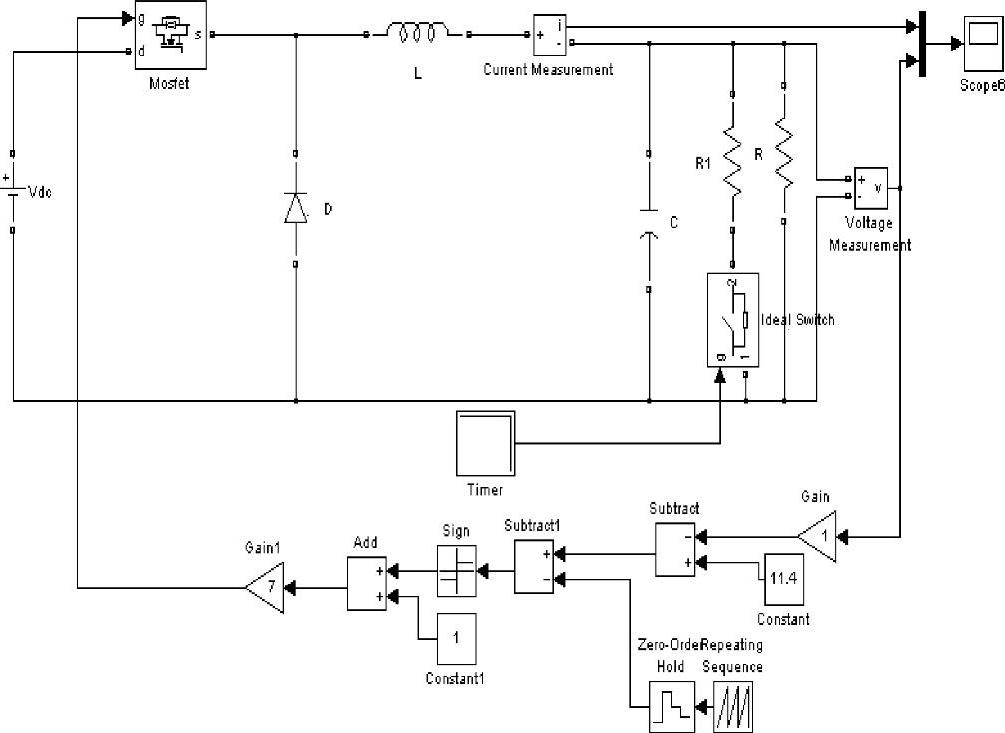
图1-8 开关调节系统负载突变的仿真模型

仿真实验测得：输出电压上冲值ΔU=1.56V，调节时间t_s=1.2ms，超调量σ=13.4%，稳态时的平均电感电流i_Lav=1.8A。

系统卸载过渡过程瞬态响应表明，卸载前后，电感上的能量差为L（I²_1-I²₂）/2。这些能量只能向电容释放，电容的电压随之上升，因此输出电压会产生上冲。(www.daowen.com)

仿真实验2：输出电流的初始值I₁=1.8A，突增到I₂=5.8A。突增负载时的仿真模型如图1-8所示，只是系统启动以后达到稳态（约2ms），设置理想开关在初始时断开，而在加载瞬间（4ms处）闭合。这样，在加载前，负载电阻为R；加载后，负载电阻为R′=R∥R₁（R′＜R）。加载瞬间的瞬态响应曲线如图1-10所示，图中曲线1为输出电压瞬态响应，曲线2为电感电流瞬态响应，可见，加载瞬间输出电压下冲，而电感电流上升。

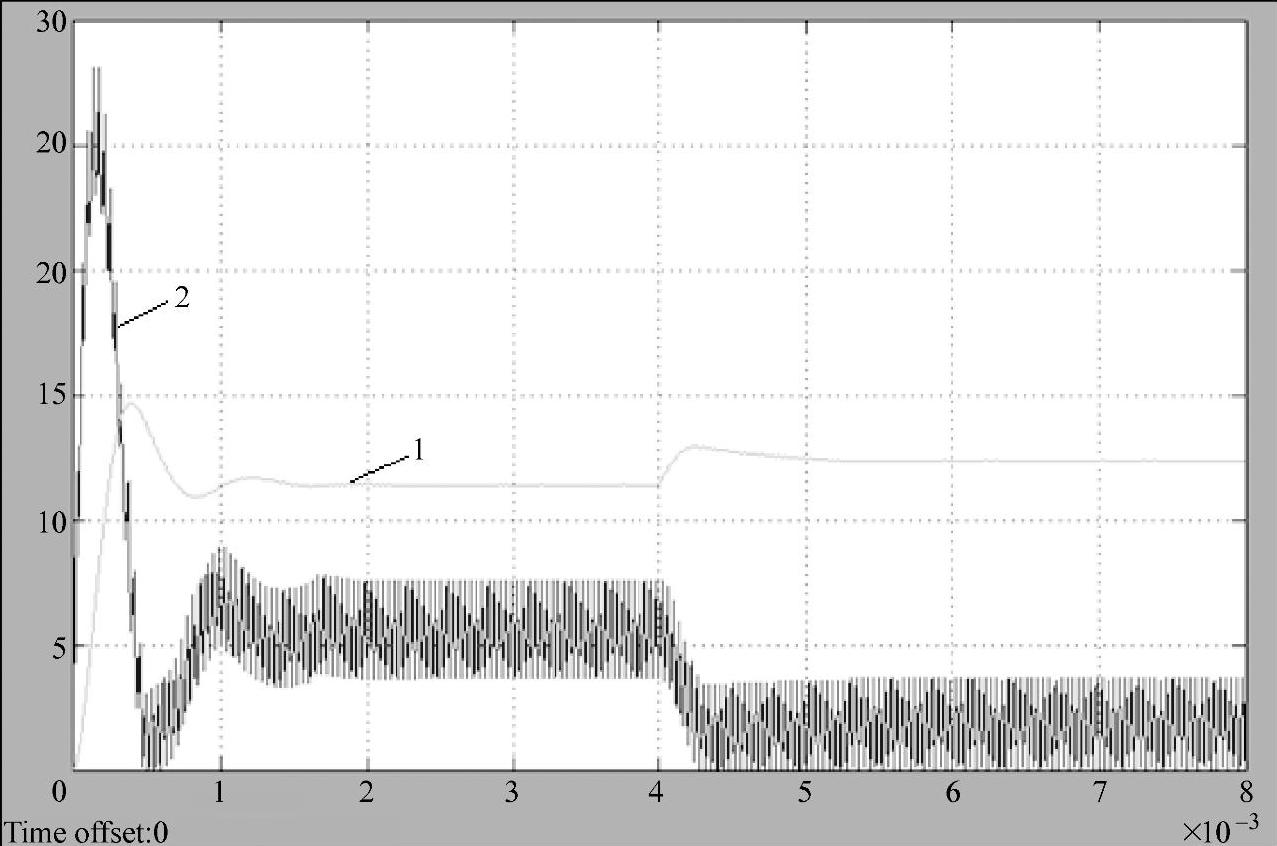
图1-9 在4ms突卸负载时的瞬态响应曲线

1—输出电压 2—电感电流

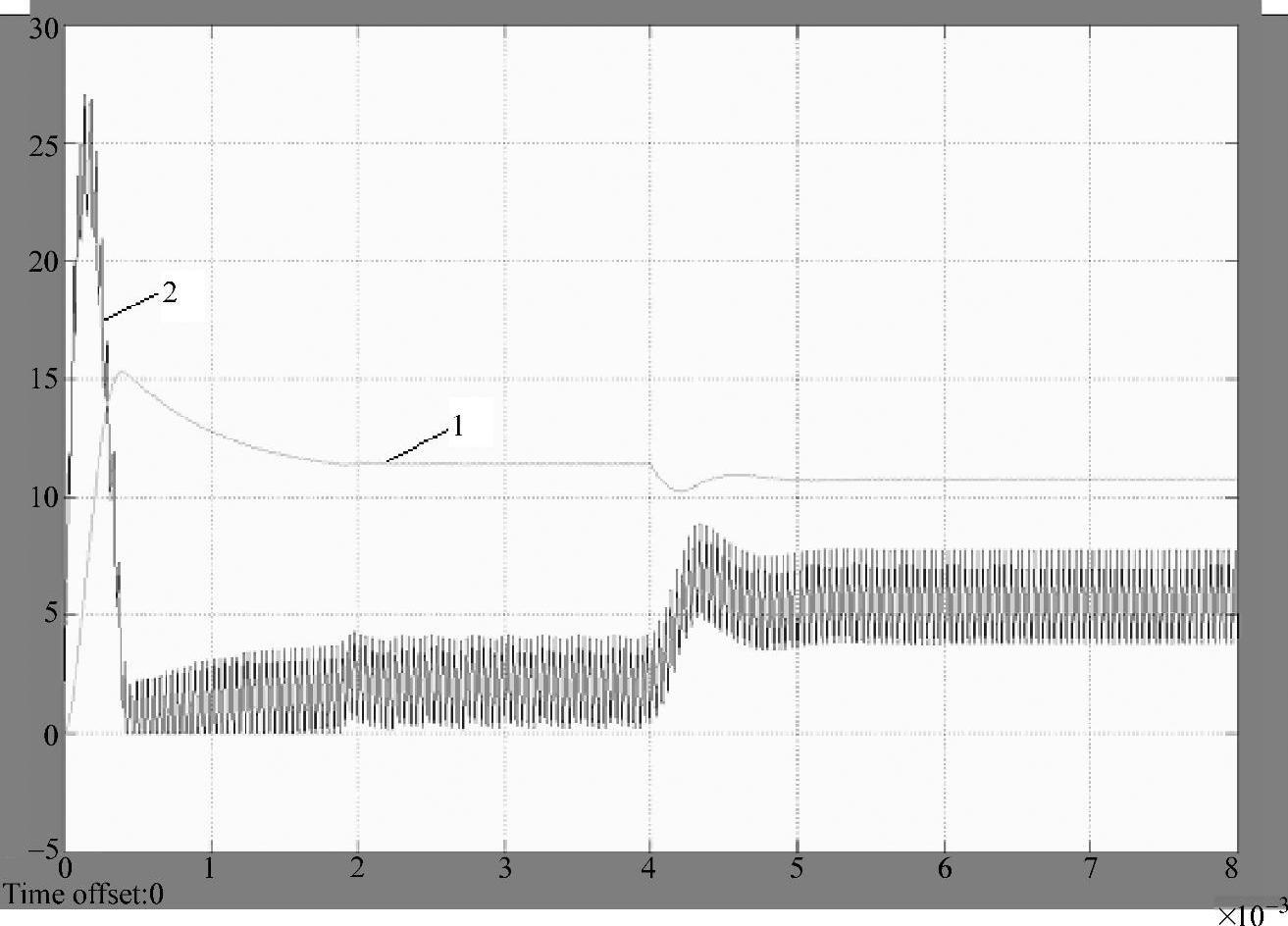
图1-10 在4ms突增负载时的瞬态响应曲线

1—输出电压 2—电感电流

仿真实验测得：输出电压下冲值ΔU=1.15V，调节时间t_s=2ms，超调量σ=10.1%，稳态时的平均电感电流i_Lav=5.8A。

由于电感中的电流不能突变，系统提供的能量小于负载所需的能量，不足的部分由电容提供，因此输出电压会产生一个ΔU=1.15V的下冲，超调量σ=10.1%。系统加载后，输出电压降低，控制电路使输出的占空比为最大值D_max，此时系统以最大的输出能力向负载提供能量。同时，电感电流会有一个很大的9A的过冲值。但因受系统的速度限制，使输出电压仍有下冲，故减小下冲与控制电路无关，而应减小主电路的阻尼系数，使系统的响应速度提高。

4.开关调节系统电源突变的过渡过程分析

为了使开关调节系统在大信号扰动下能够可靠工作，深入研究各种情况下的大信号瞬态特性是十分重要的。下面研究电源电压突变时开关调节系统的过渡过程。

仿真实验1：上述Buck变换器开关调节系统，带恒定负载运行，使电源电压由24V突降到17.05V，仿真输出电压和电感电流的瞬态响应。仿真模型如图1-11所示，系统启动以后达到稳态（约2ms），设置电源电压在4ms处突降，瞬态响应如图1-12所示。图中曲线1为输出电压瞬态响应，曲线2为电感电流瞬态响应，可见，电源电压突降瞬间输出电压下冲，电感电流下降。

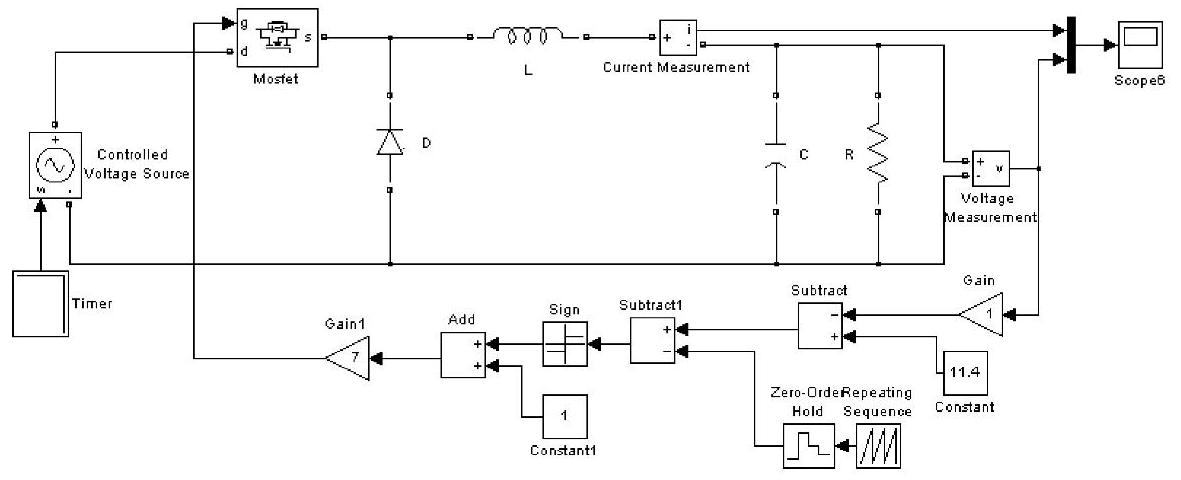
图1-11 开关调节系统电源电压突变时的仿真模型

仿真实验测得：输出电压下冲值ΔU=2.95V，调节时间t_s=2ms，超调量σ=25.9%，输出电压最终稳定在9V，稳态时的平均电感电流i_Lav=2.3A。

电源电压突降瞬间，电感电流减小，系统提供的能量小于负载所需的能量，不足的部分由电容提供，因此输出电压会产生一个ΔU=2.95V的下冲，产生超调量为25.9%，输出电压降低，控制电路使输出的占空比为最大值D_max，此时系统以最大的能力向负载提供能量。同时，电感电流会逐渐增大，直到稳态。电源电压降低后，电源提供的能量不足以维持输出所需的能量，因此输出电压最终稳定在9V。

仿真实验2：对上述Buck变换器开关调节系统，带恒定负载运行，使电源电压由17.05V突增到24V，仿真输出电压和电感电流的瞬态响应。仿真模型如图1-11所示，系统启动以后达到稳态（约2ms），设置电源电压在4ms时突增，瞬态响应曲线如图1-13所示。图中曲线1为输出电压瞬态响应，曲线2为电感电流瞬态响应，由图可见，电源电压突增瞬间输出电压上冲，电感电流上升。

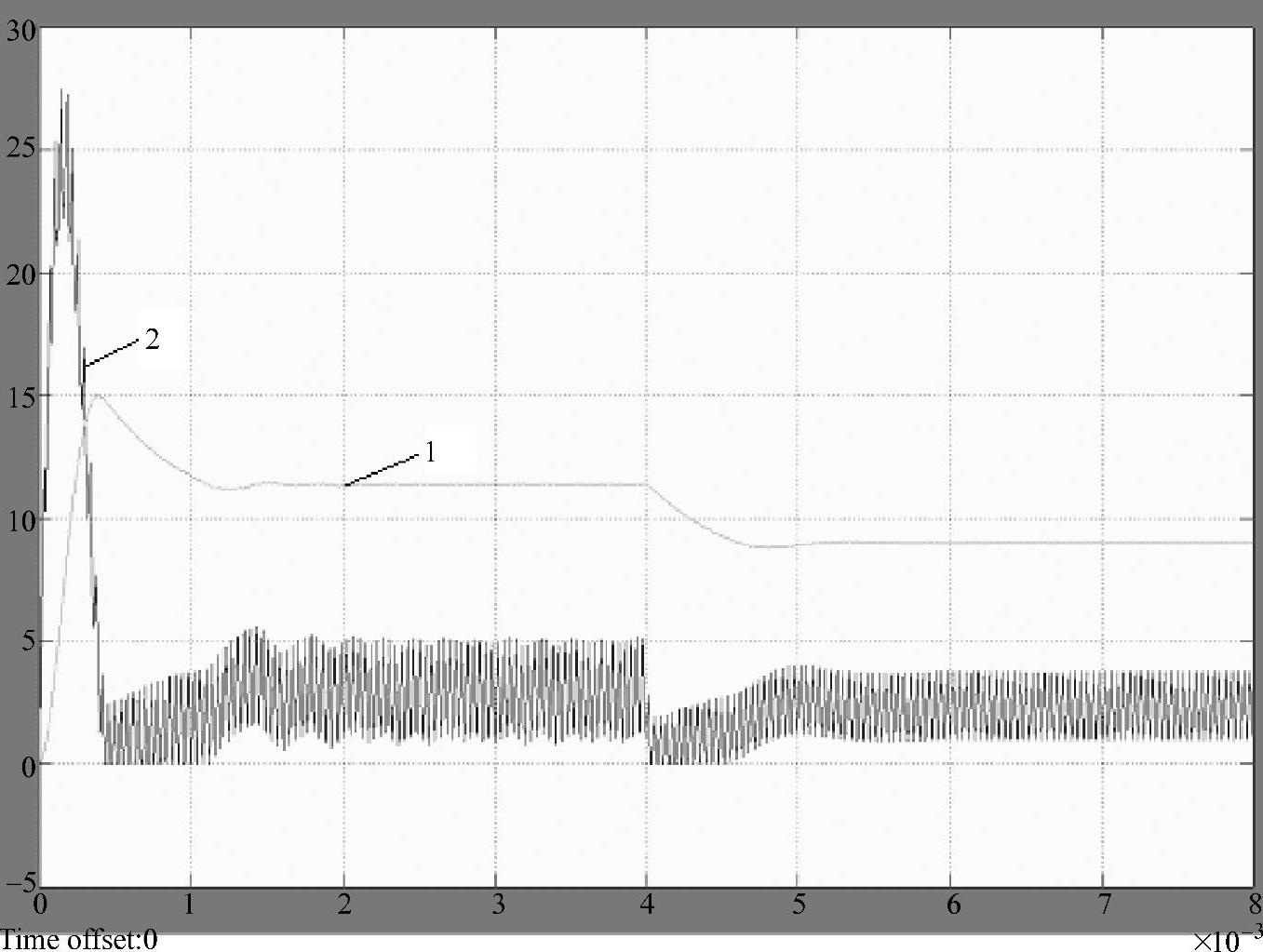
图1-12 开关调节系统在4ms电源电压突降时的瞬态响应曲线

1—输出电压 2—电感电流

仿真实验测得：输出电压上冲值ΔU=4.12V，调节时间t_s=2ms，超调量σ=36.1%，输出电压最终稳定在14.4V，稳态时的平均电感电流i_Lav=3.7A。

突增电源电压瞬间，由于电源电压的上升，使电感电流增大，系统提供的能量大于负载所需的能量，多余部分给电容充电，因此输出电压会产生一个ΔU=4.12V的上冲，超调量为36.1%，输出电压升高，最终稳定在14.4V上。

由上面的仿真实验可见，不论负载突变或电源电压突变，要想使输出电压维持在11.4V上，简单的反馈控制是不够的，还要研究控制策略和设计相应的控制器，才能达到稳压的目的，关于开关调节系统的控制策略将在本书第2章中介绍。

5.开关调节系统输出端突然开路的过渡过程分析

上述Buck变换器开关调节系统处于满功率工作时，对负载突然开路进行仿真实验，其MATLAB仿真模型如图1-14所示。设置系统正常运行时理想开关在闭合位置，而开路瞬间（4ms时）断开，其瞬态响应曲线如图1-15所示。图中，曲线1为输出电压瞬态响应，曲线2为电感电流瞬态响应，由图可见，输出电压以指数规律上升，直至接近输入电压。

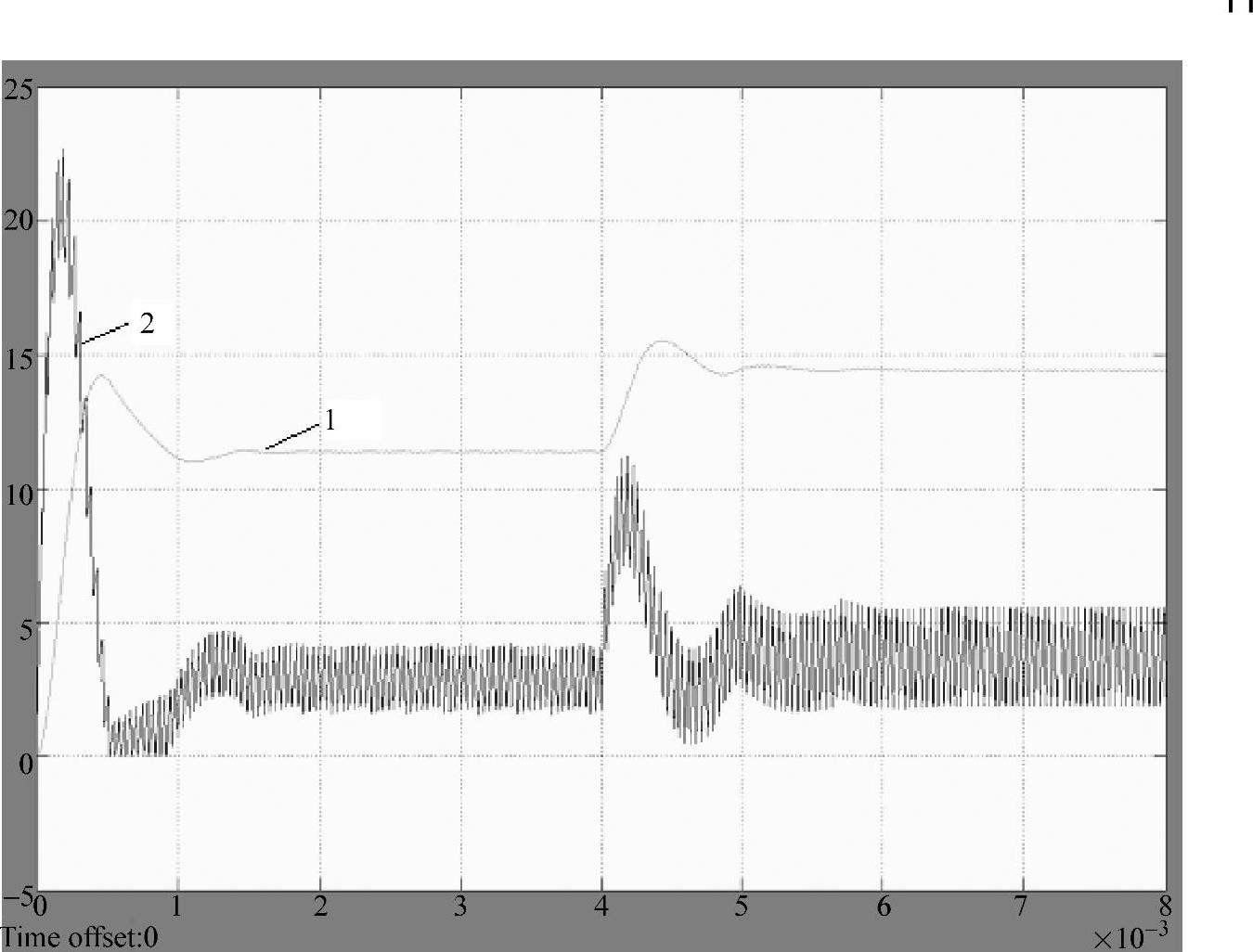
图1-13 开关调节系统在4ms电源电压突升时的瞬态响应曲线

1—输出电压 2—电感电流

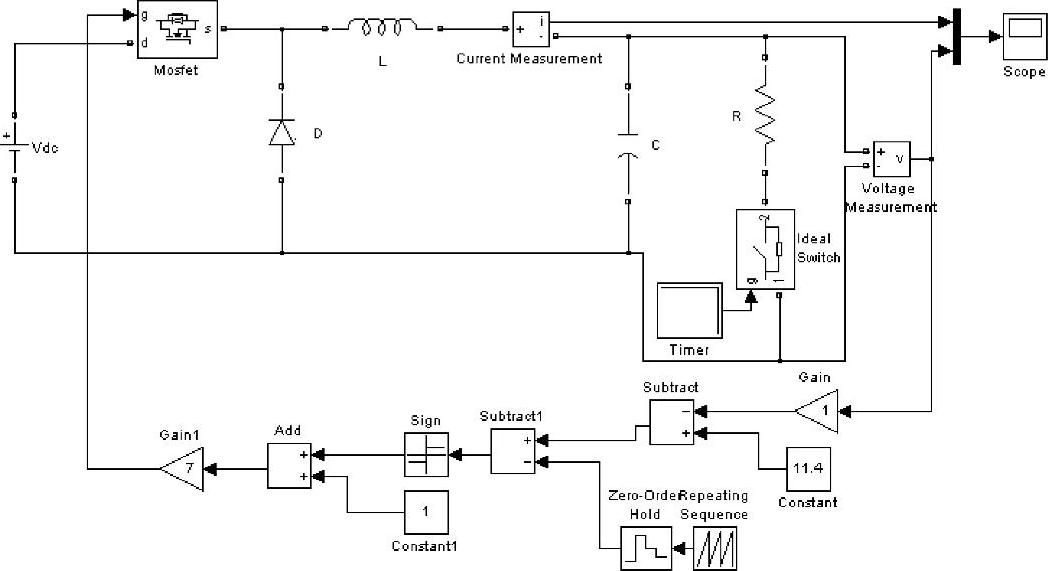
图1-14 开关调节系统输出端突然开路时的仿真模型

仿真实验表明：开关调节系统处于满功率运行时负载突然开路，储存在滤波电感中的能量将向电容充电，使输出电压骤然升高，其值趋于输入电压24V，这将使后级电路因过电压而损坏。为了防止变换器突然开路，应增设输出过电压保护以及假负载。其中，过电压保护的作用是，当电压过高时，强迫开关管截止，停止能量的传输，而假负载的作用是保证电路正常工作，使输出电压维持其额定值。

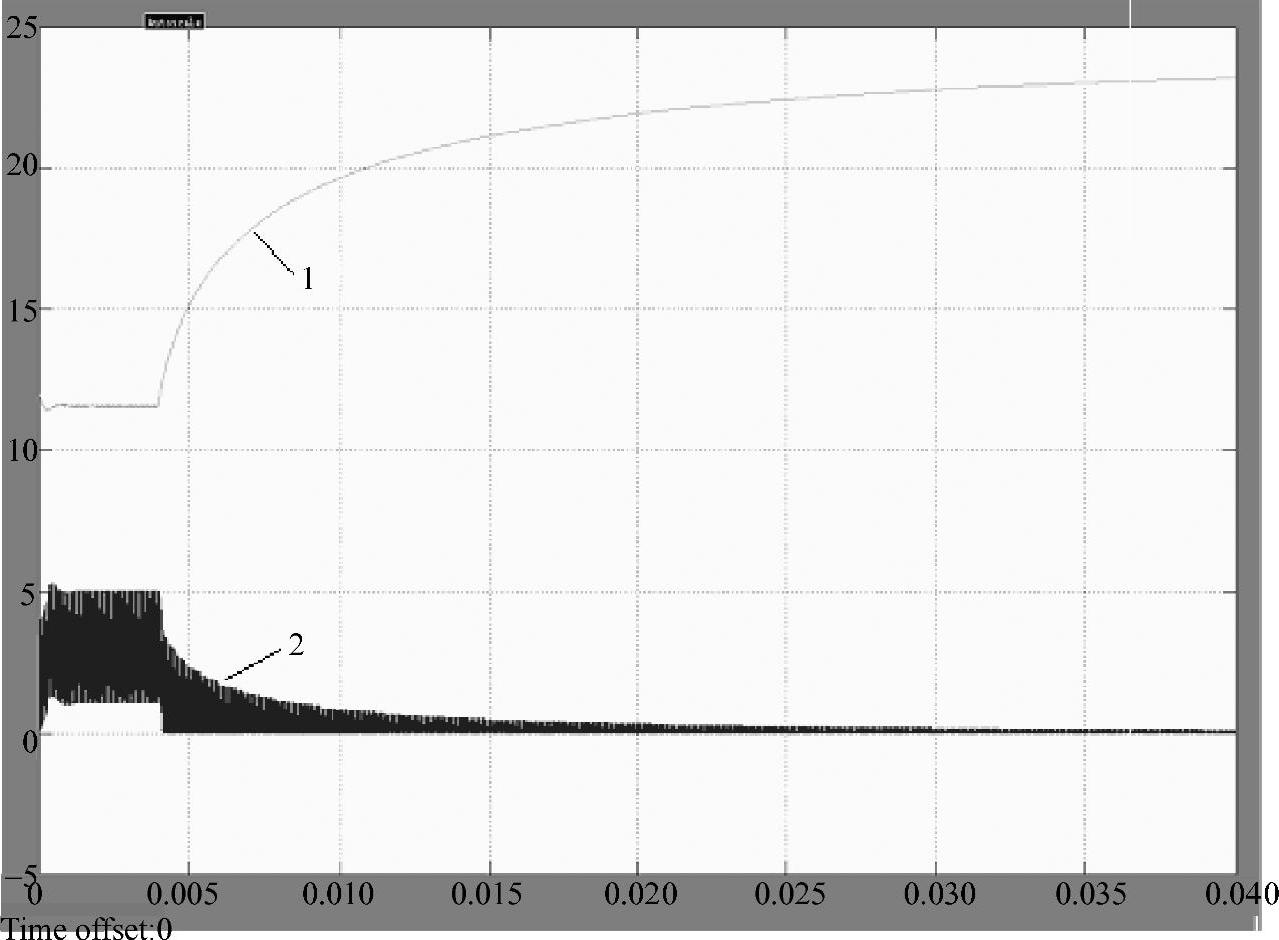
图1-15 开关调节系统输出端突然开路的瞬态响应曲线

1—输出电压 2—电感电流

6.开关调节系统输出端突然短路的过渡过程分析

上述Buck变换器开关调节系统处于满功率运行时，对输出端突然短路进行仿真实验，其仿真模型如图1-16所示。设置系统正常运行时理想开关在断开位置，而短路瞬间（4ms时）闭合，其瞬态响应曲线如图1-17所示。图中，曲线1为输出电压瞬态响应，曲线2为电感电流瞬态响应。

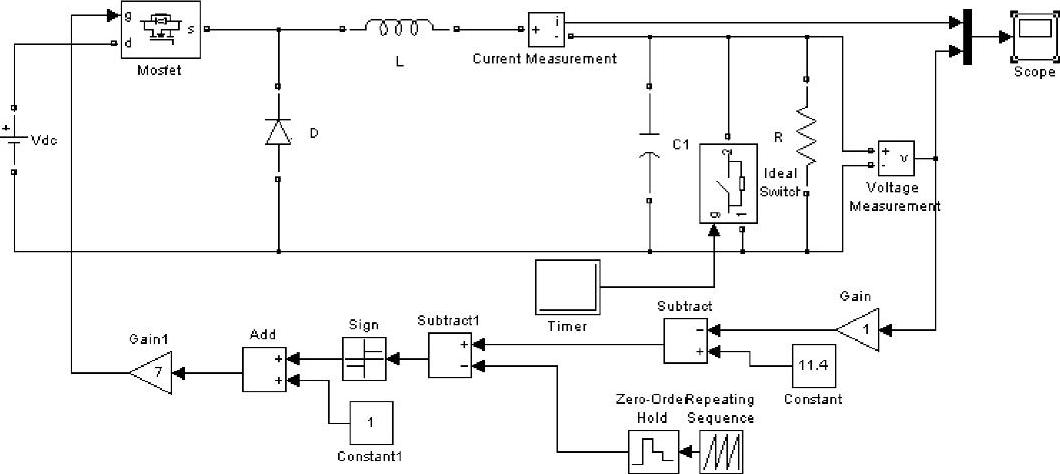
图1-16 开关调节系统输出端突然短路的仿真模型

仿真实验表明：开关调节系统处于满功率运行时输出端突然短路，使输出电压为零。由于输出电压为零，使脉宽调制器的输出为最大占空比D_max，电感电流单调上升，其上升速度与电感量、开关频率以及输出电压有关。仿真实验测得电感电流最大值为62.3A。这样巨大的短路电流会使电感铁心达到饱和而烧毁主电路。因此要增设过电流保护，一般限制电感电流为额定值的1.2～1.5倍。

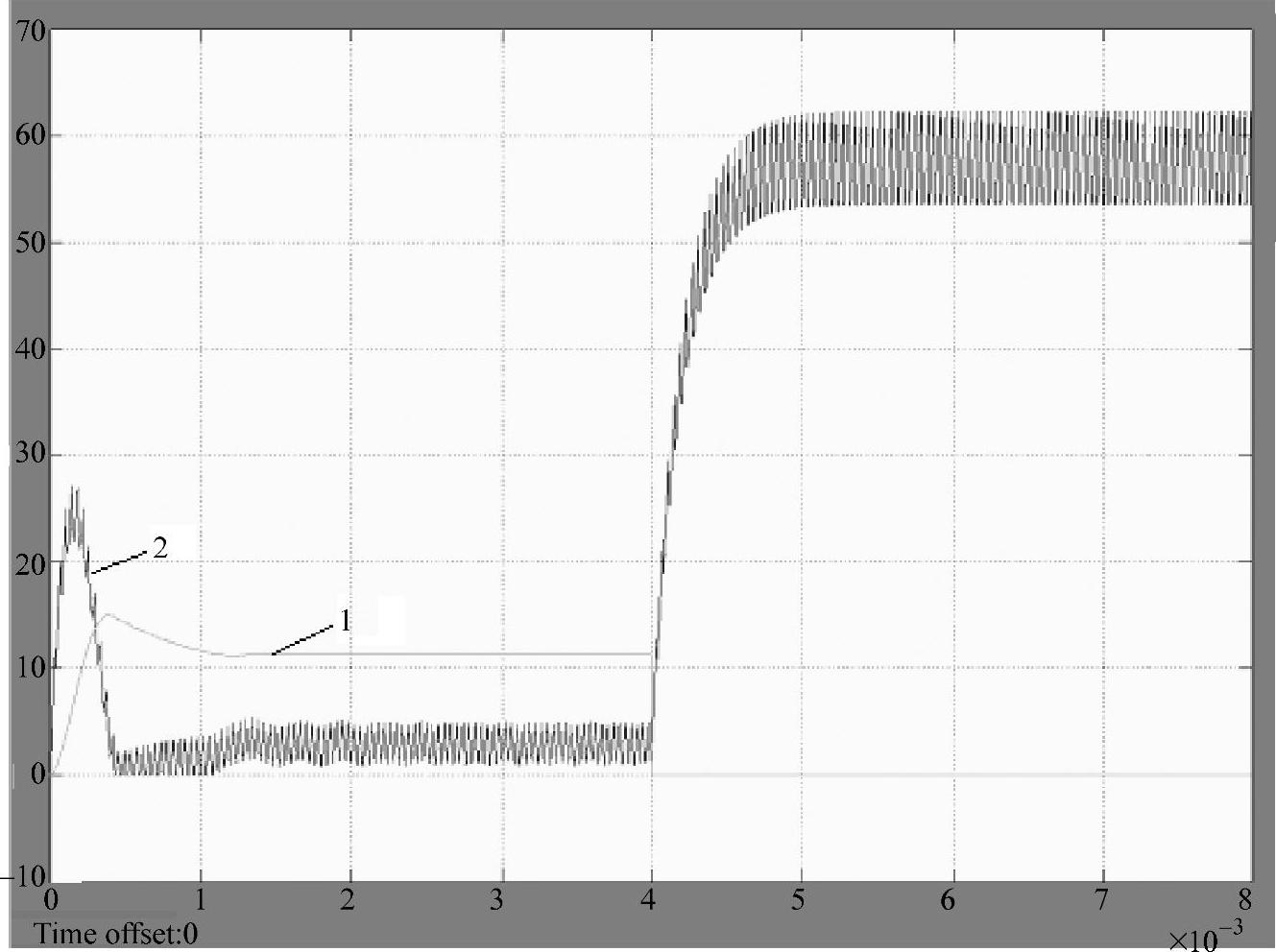
图1-17 开关调节系统在4ms输出端突然短路时的瞬态响应曲线

1—输出电压 2—电感电流

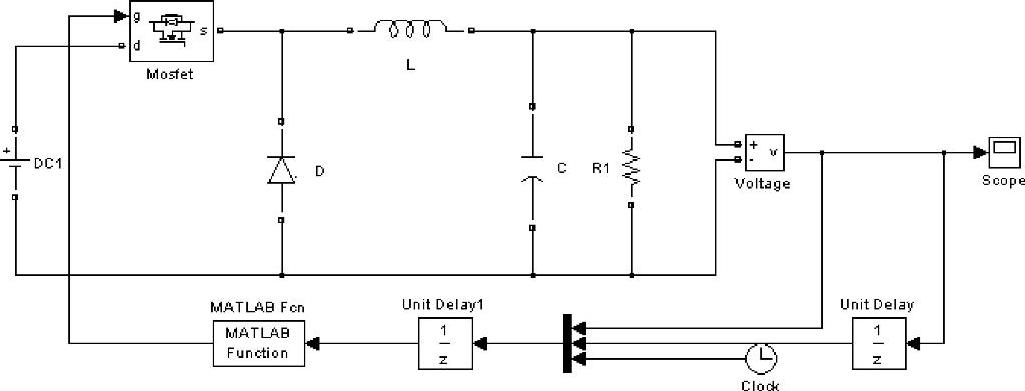
图1-18 开关调节系统软启动仿真模型

7.开关调节系统软启动实验

为了限制开关调节系统启动过程中输出电压上升速度过快，控制电路要增设软启动功能，控制占空比由零逐渐增大，然后进入稳态，模拟开关调节系统软启动的仿真模型如图1-18所示，其中软启动算式为d=（1+0.4i）%，用C语言编制软启动程序嵌入到MATLAB Fcn模块中，可得到软启动瞬态响应曲线如图1-19所示。

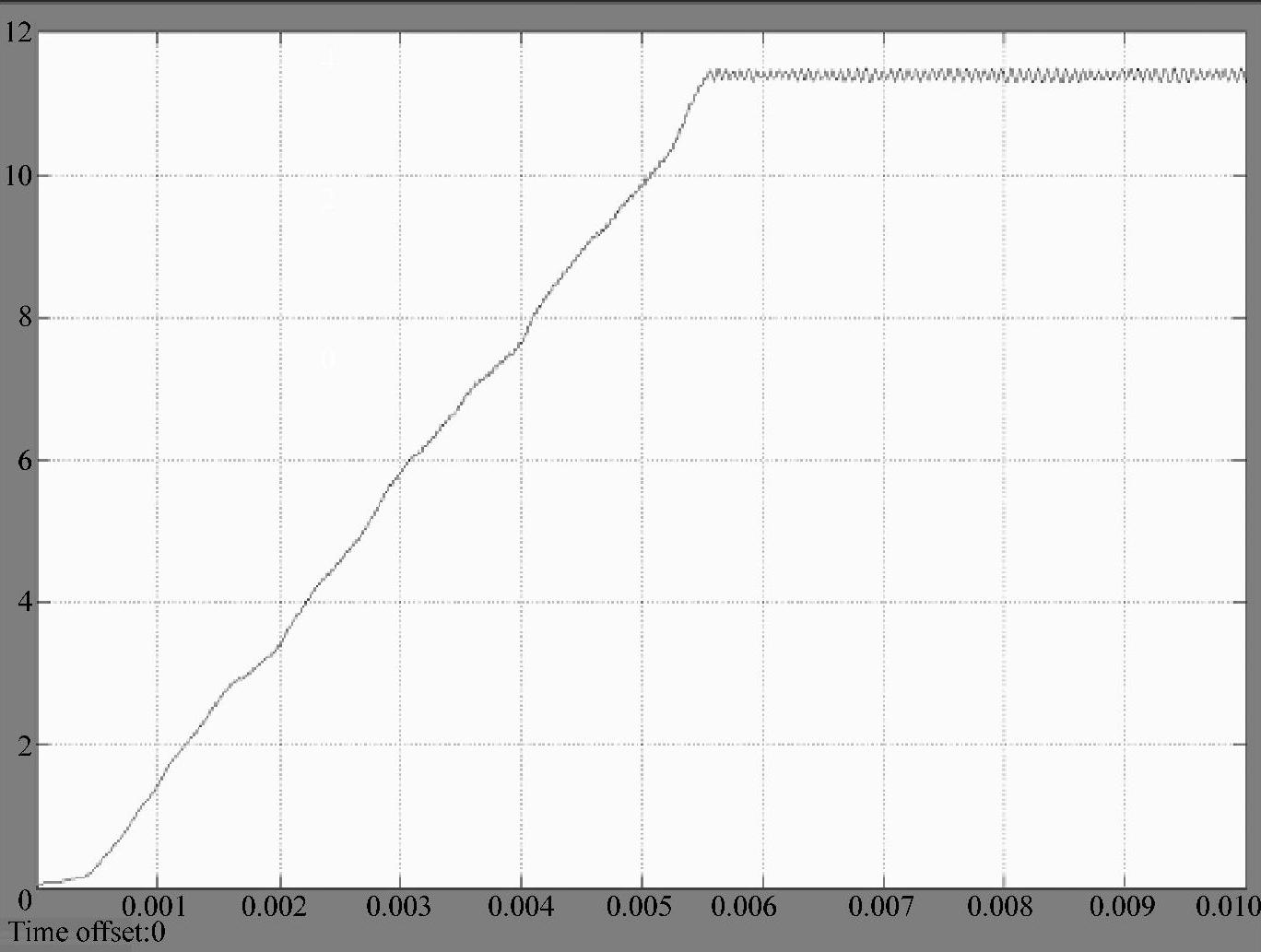
图1-19 开关调节系统软启动瞬态响应曲线

仿真实验测得：经139步（i=138），启动时间t=139×0.04ms=5.56ms后，软启动结束，系统进入稳态，输出电压达到11.4V的额定值，避免了启动过程中产生输出电压过冲，减少了由于开关调节系统启动对主电路和电网产生的不良影响。