【摘要】:从传递函数的角度来看,位置控制器相当于一个比例环节,其比例系数是KP。将各环节的传递函数代入图3-66中,就得到了系统的动态结构图,如图3-67所示。在图3-67中,前向通道的传递函数图3-67进给伺服系统动态结构图利用前向通道的传递函数GK,可将图3-67简化为图3-68。由此可见,半闭环进给伺服系统是一个典型的二阶系统。其中无阻尼自然角频率ωn为系统的阻尼比ξ 为将ωn和ξ 代入式得
进给伺服系统的结构框图如图3-66所示。
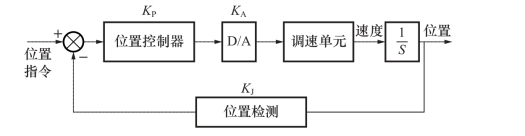
图3-66 进给伺服系统的结构
在图3-66中,位置控制器执行比例控制算法。控制器本身可以是微处理器,也可以是由硬件构成的脉冲比较电路或相位比较电路。从传递函数的角度来看,位置控制器相当于一个比例环节,其比例系数是KP。
位置控制器输出的是数字量,必须经过D/A 转换之后才能控制调速单元,D/A 转换也相当于一个比例环节,其比例系数是KA。
从位置环角度来看,调速单元可以等效为一惯性环节KV/(TVS+1),式中TV为惯性时间常数,KV为调速单元的放大倍数。
调速单元的输出量是速度,这一速度信号经过积分环节l/S 后成为角位移信号。
位置检测环节是指位置传感器和后置处理电路。这个环节也可以看作一个比例环节,其比例系数是KJ。
将各环节的传递函数代入图3-66中,就得到了系统的动态结构图,如图3-67所示。在图3-67中,前向通道的传递函数
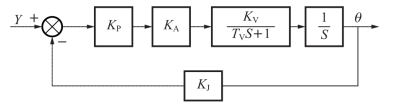
图3-67 进给伺服系统动态结构图
![]()
利用前向通道的传递函数GK(S),可将图3-67简化为图3-68。因此图3-68所示系统的闭环传递函数为(www.daowen.com)
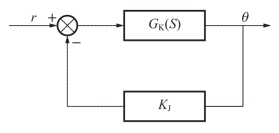
图3-68 简化的动态结构图
![]()
将GK(S)代入得
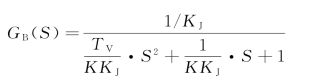
式中 K=KPKAKV。
由此可见,半闭环进给伺服系统是一个典型的二阶系统。
其中无阻尼自然角频率ωn为
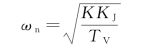
系统的阻尼比ξ 为
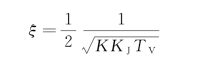
将ωn和ξ 代入式(3-24)得
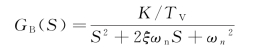
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
有关数控加工工艺与编程的文章








