应该注意到，前述方法仍为弦长逼近弧长的插值方式，因此，同样会存在弦高误差e_k+1，e_k+1应为参数u的函数e_k+1（u），可计算为

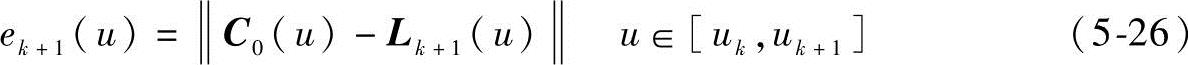
式中，L_k+1（u）表示C₀（u_k）和C₀（u_k+1）所形成线段的矢量函数表达式，即有

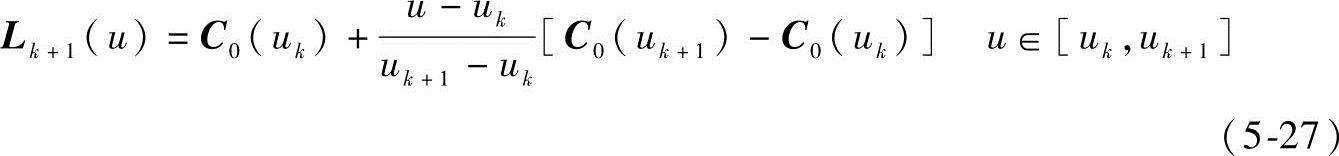
式（5-26）为插值算法的理论误差模型，通过求一阶导并令其为0的方法可以求得最大插值误差E_k+1。但这种方法计算比较复杂，考虑到C₀（u_k）和C₀（u_k+1）形成的弦已经为微小线段，因此可采用下述曲率圆逼近方法近似求得最大插值误差（见图5-13）。

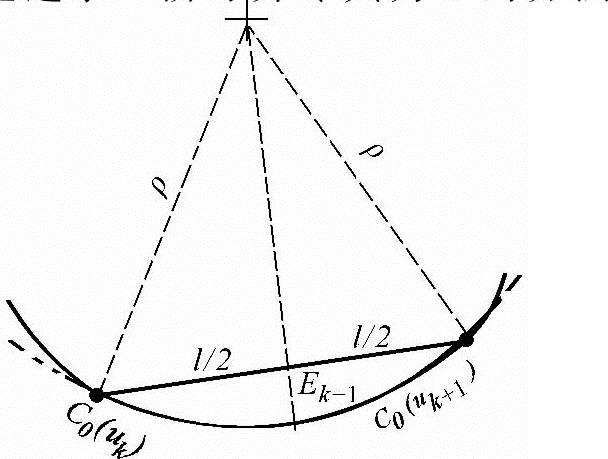
图5-13 插值误差计算模型

由图5-13可得

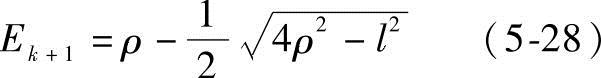
式中，l为C₀（u_k）和C₀（u_k+1）形成的弦长；ρ取为C₀（u_k）和C₀（u_k+1）处曲率半径ρ_k和ρ_k+1的平均值。

1.样条段内速度自适应控制

由式（5-28）可知：①在等弦长的情况下，样条曲线曲率较大（曲率半径ρ较小）的地方插值误差也较大；②在曲率（或曲率半径）一定时，弦长越长对应的插值误差越大。在待插值样条曲线一定的情况下，曲线曲率已无法调整，因此，要降低插值误差就只能通过缩短弦长的方法实现。又由式（5-26）可知，较小的进给速度对应较短的弦长，如果采用参考文献[115]的等进给速度方法进行插值，则各插值周期内进给弦长近似相等，这将导致在大曲率的地方产生较大的插值误差。因此，需要对各个插值周期的进给速度进行自动调整以消除曲率大小的变化对插值误差的影响。

假定允许的轮廓控制误差为ε，插值指令F指定的进给速度为υ（即沿样条曲线加工时所能达到的最高速度），则所有插值周期的插值误差E_k中的最大值E_max必须满足如下不等式

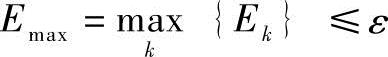
由于样条曲线给定的情况下，插值误差最大值E_max在进给速度最高（υ）、曲率半径最小（ρ_min）时取得，令式（5-28）中l＝υT_s，ρ＝ρ_min，则有

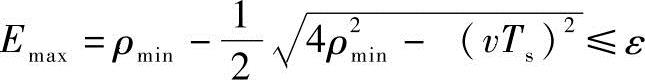
所以

上式表明，要使样条插值时的插值误差满足加工要求，曲率半径ρ应不小于ρ₀，若小于该值时可能导致曲率过大而损失插值精度。而当ρ小于ρ₀时，则需要对进给速度进行实时调整。调整方法如下：

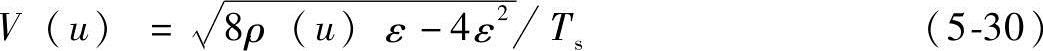
2.加减速控制原理

程序段之间过渡转接时为减少速度变化弓起的加速度冲击，一般需进行加减速处理。常见的加减速类型有线性加减速、指数加减速以及S型加减速，本书以线性加减速为例说明。

假定系统参数指定的加（减）速度为a，加速结束时的目标速度为F指令指定的速度υ，如图5-14所示。

进行加减速规划的关键是减速点的预测，而减速点预测的关键则是减速距离的计算。如图5-14所示，阴影三角形的面积S_D即表示减速距离。

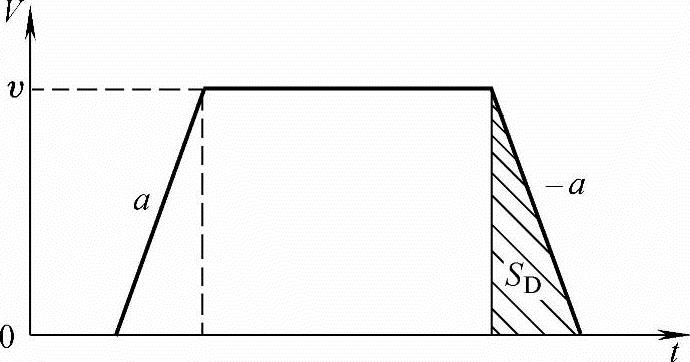
图5-14 线性加减速模型

需要根据S_D求出提前减速点的参数值u_D。由于减速目标点为样条程序段的终点，在该点处参数值为1，因此有

式（5-32）很难进行解析方法的求解。这里采用如下牛顿迭代法^[136]（该方法在根的附近具有平方收敛性）来求解u_D。

设

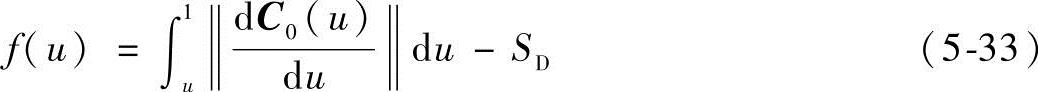
则有f（u_D）＝0。设u_D的初始值为u₀＝1，此时f（u₀）＝-S_D，则有如下递推表达式

u_i+1＝u_i-f（u_i）/f′（u_i）i≥0 （5-34）

式中，i取为整数。式（5-34）等价于

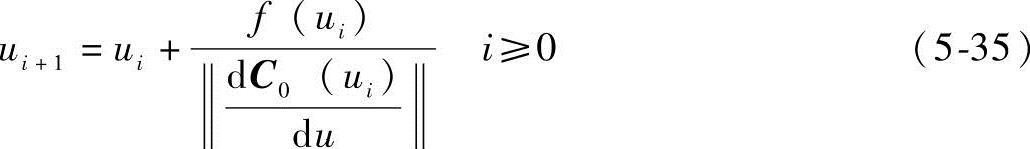
式（5-34）和式（5-35）中f（u_i）的求取可采用复化辛普森（SimPson）积分方法^[136]得到，停止迭代计算的条件为

式中，η为迭代误差。当式（5-36）的条件成立时，表明u_i+1已足够接近u_D，令u_D＝u_i+1即可。

3.速度处理与控制的流程

通过前述分析，可将五轴NURBS插值过程中的进给速度前瞻控制规划如下：

1）样条程序段译码后，初始化相关数据并计算减速点对应的参数和满足精度条件下的最小曲率半径。

2）分析当前插值点所处的区域（如加速区、减速区等），预先估算出下一插值点对应的参数并计算该点曲率半径。

3）判断计算出的曲率半径是否过小：如是则计算该曲率半径对应的进给速度，重新计算下一个插值点；如否则计算刀轴单位矢量并计算该矢量对应的旋转运动坐标。(www.daowen.com)

4）判断是否到达程序段终点，如否则转至第2）步，如是则表示到达程序段终点结束插值运算。

具体流程如图5-15所示。

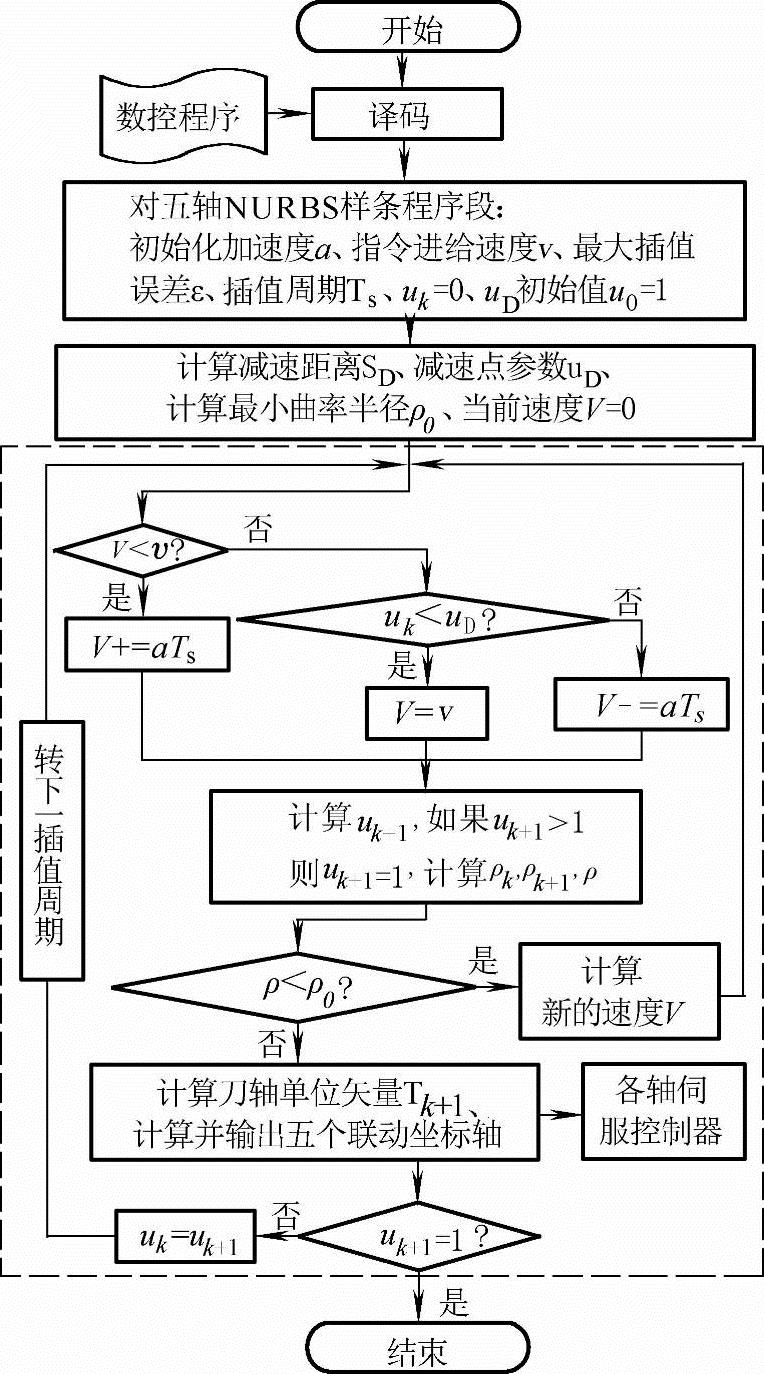
图5-15 速度前瞻控制流程图

4.速度控制实例计算与对比分析

假定某个待加工零件的五轴数控加工程序中包含有如下NURBS样条程序段：

N30 G06.5 P3

X0 Y50 Z0 U0 V50 W10 R1 K0 F12000

X28.712 Y58.383 Z12.236 U29.338 V56.961 W20.758 R1 K0

X45.157 Y58.2 Z0.78 U42.235 V60.36 W11.189 R1 K0

X57.900 Y59.827 Z16.631 U61.276 V63.167 W25.335 R1 K0

X55.853 Y46.203 Z2.726 U55.158 V51.230 W10.852 R1 K0.366

X55.652 Y34.154 Z10.46 U52.334 V38.561 W19.150 R1 K0.509

X52.889 Y11.480 Z3.640 U48.352 V13.576 W12.263 R1 K0.646

X50 Y0 Z0 U50 V0 W10 R1 K0.746

K1

K1

K1

K1

由F指定的进给速度为12000mm/min（200mm/s）。该段代码对应的刀心点轨迹如图5-16所示，轨迹曲线曲率最大的地方对应的曲率半径为1.012mm。初始化加工参数如下：a＝2000mm/s²、T_s＝2ms、ε＝1μm、η＝0.001，经译码程序计算可得ρ₀＝20mm，u_D＝0.926。

分别采用参考文献[115]实现的方法和本书提出的速度控制方法实时插值前面给出的五轴NURBS程序段，将相关数据（如插值误差、进给速度以及插值运算时间等）采集后绘制成变化趋势曲线图（见图5-17~图5-22）。

如图5-17所示，参考文献[115]的方法在曲率半径较大（如大于ρ₀）时，插值轮廓误差还比较小，但是当曲率半径小于ρ₀时（尤其是在最小曲率半径处），插值误差却变得很大，达不到最终的加工要求。而本书提出的方法由于根据误差要求来计算插值点，因而可以较好地适应插值轨迹局部曲率的变化，从图5-18可以看出，经过速度自适应调整并修正后可以确保插值误差始终小于ε。

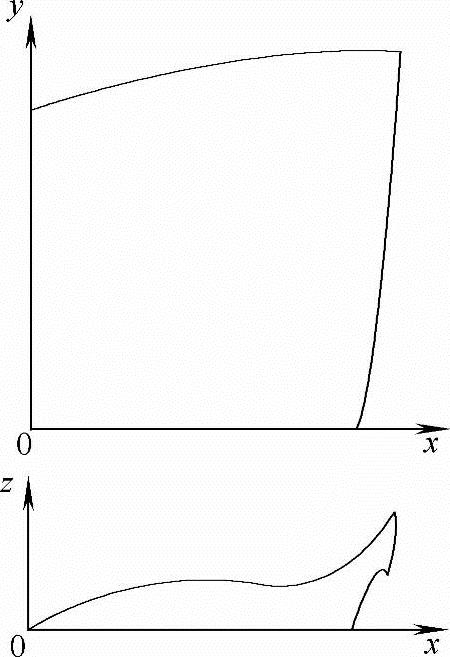
图5-16 待插值代码对应的刀心点轨迹（单位：mm）

图5-19表示的是采用参考文献[115]时进给速度的变化曲线。从该图中可以看出由于没有进行速度规划，插值输出的进给速度比较平稳，只是在曲率变化较大的地方略有波动（＜5%）。本书提出方法的进给速度曲线如图5-20所示，在曲率半径小于ρ₀时，为了保证插值轮廓精度进行了适当的降速处理，而巨在曲率最大的地方降速的幅度也最大。另外还需注意到本书的方法在程序段的起点和终点处还添加了加减速控制环节。译码程序对u_D的大小进行了非实时前瞻规划后，能使得程序段之间的速度过渡转接更加平稳，尽可能地减轻了机械冲击。图5-21所示为本书提出方法在进给速度变化时产生的加速度，加速度最大值达到了7m/s²，接近1个重力加速度g（9.8m/s²）。因此，如果机床可承受的最大加速度较小时（如0.5g），还需在本书方法的基础上进一步限制加速度的大小。

图5-22对两种方法的运算消耗时间进行了对比。参考文献[115]的方法由于需要实时运算的任务量较小，因此插值计算速度也较快，而本书提出的方法由于添加了速度规划和处理环节后实时插值计算的任务较多，插值运算的时间有所增加（增加了60μs左右），但总的来看运算的时间（约90μs左右）对于常见系统毫秒级的插值周期而言还是足可以保证系统实时性要求的。

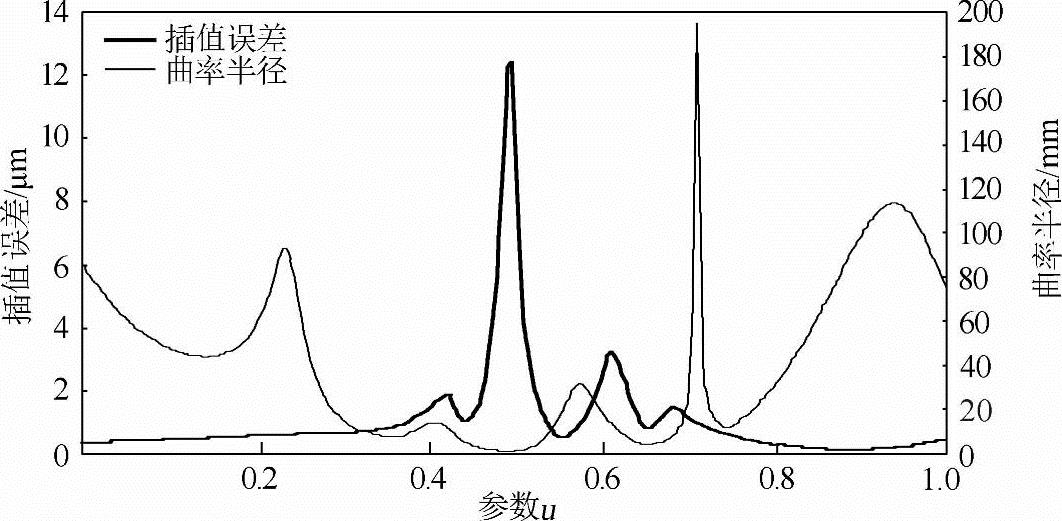
图5-17 参考文献[115]方法的插值误差

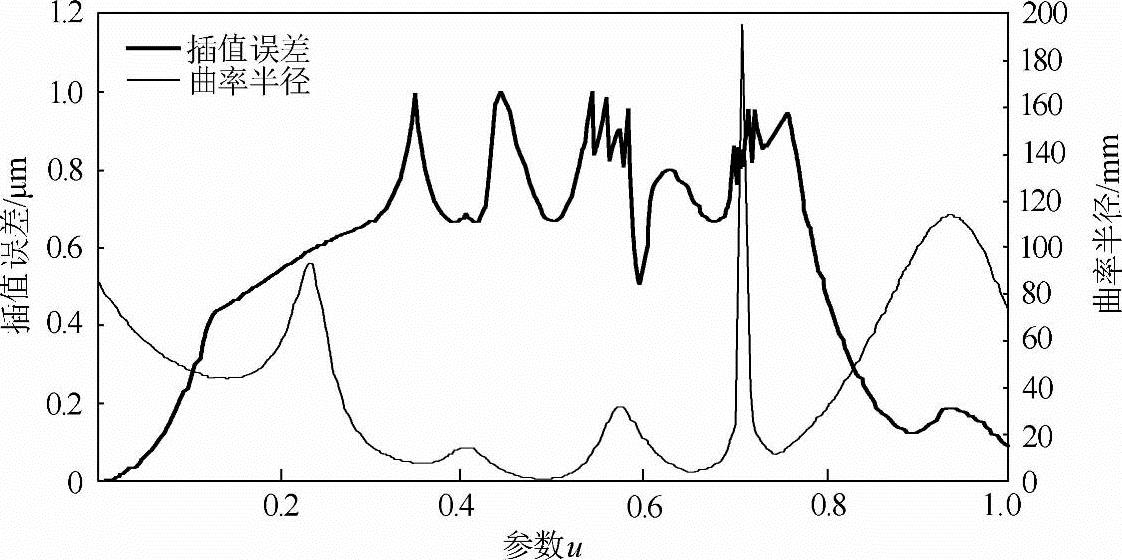
图5-18 本书提出方法的插值误差

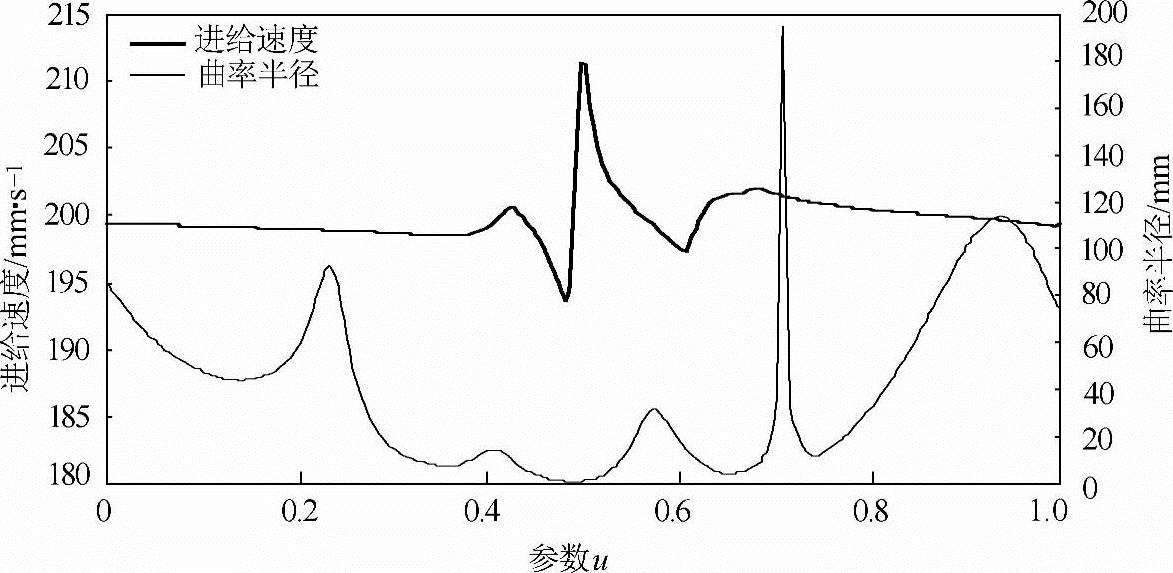
图5-19 参考文献[115]方法的进给速度

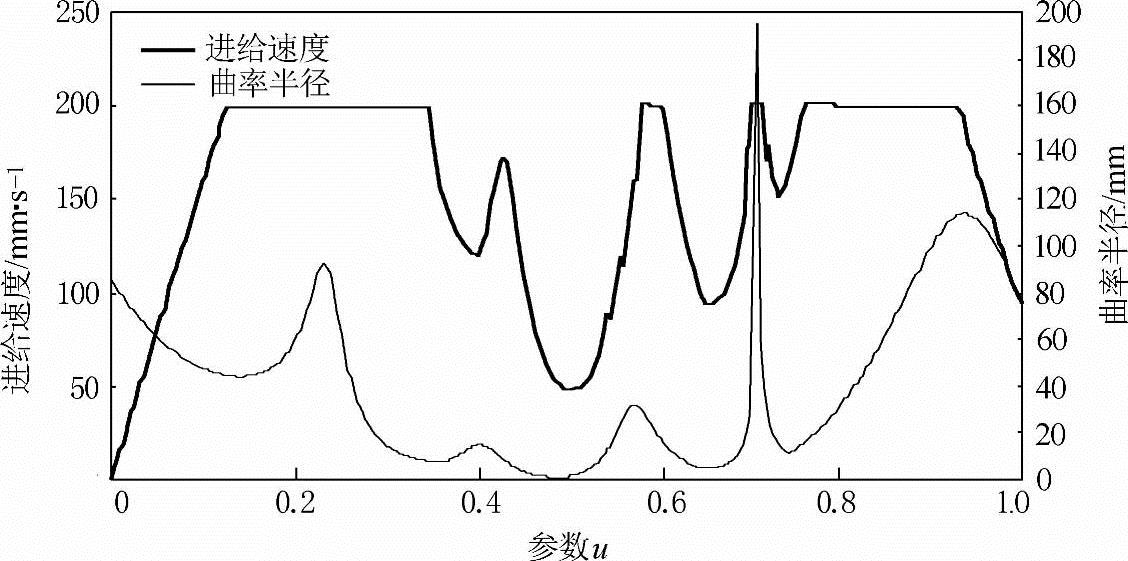
图5-20 本书提出方法的进给速度

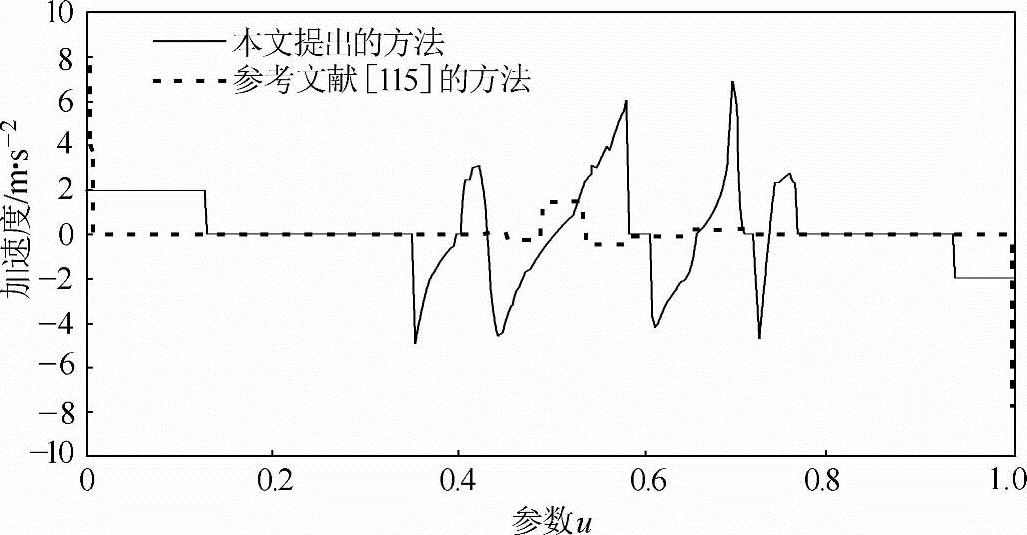
图5-21 本书提出方法的加速度

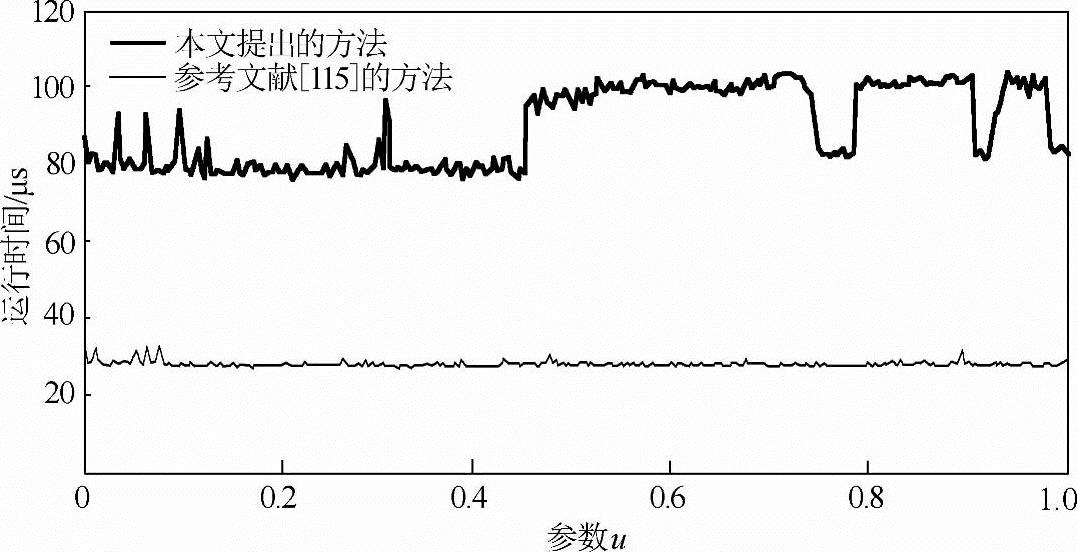
图5-22 两种方法的实时性比较

综上可得出如下三点有意义的结论：

1）等弦长进给时插值误差随着样条曲线曲率的增大而增大，而在曲线曲率一定时，弦长越大对应的插值误差也会越大。基于此，在待插值样条曲线已经确定的情况下，曲线曲率也随之确定，减小插值误差的唯一途径是通过减小进给弦长（对应进给速度）的方法实现。

2）通过建立满足插值误差要求条件下的最小曲率半径（最大曲率）与进给速度大小之间的关系，可以准确判断当前插值点和相邻的下一插值点是否满足误差要求，并可计算满足误差要求的下一插值点。应用数值分析方法可以在插值前事先计算出样条程序段的减速点，避免了实时计算当前插值点与终点间距离以判断是否到达减速点和终点，相对减轻了实时计算任务。

3）应用本书提出的速度前瞻控制方法，即便对插值轨迹曲线上的尖角处也能有效地通过进给速度的实时调整提高插值精度并满足插值误差的要求，对五轴样条插值进行加减速速度规划使得程序段间的转接更加平稳，能有效减轻转接过程中速度变化对机床的机械冲击。