（1）译码器的实现 自行研制的开放式数控系统的模块化结构如图2-5所示。由于系统的开放性，使得在其中集成五轴NURBS译码及插值器就显得比较容易，仅需修改任务生成模块及轴组模块即可实现。

任务生成模块中用到的数据结构（用C++语言描述）如图5-8所示。

typedef std：：deque＜singieStep＞singieStep_deque；

模块中添加dnurbs结构用于五轴NURBS的译码，当该模块读取到样条程序段，即读到“G06.5”时，则开辟一段存储空间给该程序段，并把段内信息提取出来。从每个运动段中提取的信息放入singieStep_deque队列中，然后被传送到轴组模块中进行实时插值。

图5-8 任务生成模块中用到的数据结构

（2）插值器的实现 双NURBS样条曲线实时插值的任务是要根据当前插值周期插值点对应的参数值u_k计算出在下一周期的参数值u_k+1，同时将得到的刀轴矢量转化为工作台的摆转运动坐标B、C（本书所用机床为工作台摆转式五轴联动数控铣床，如图5-9所示）。

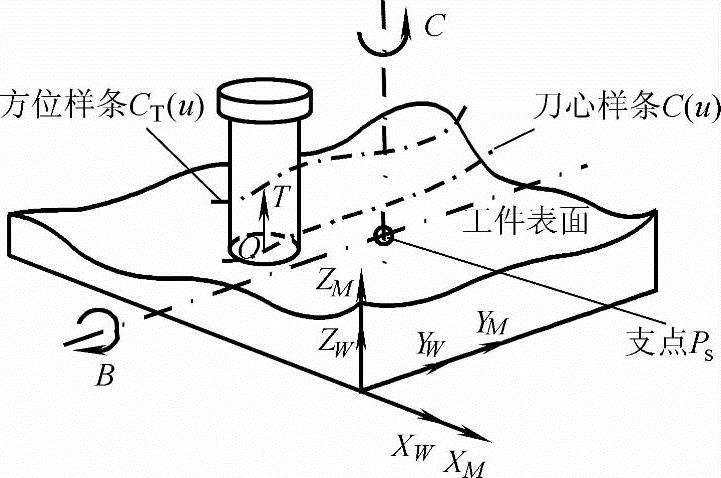
图5-9 工作台摆转式五轴CNC机床

假设某NURBS插值程序段的刀心样条和方位样条分别为C（u）和C_T（u），建立在相同的节点矢量上。时间函数u为曲线参数，并巨u（t_k）＝u_k，u（t_k+1）＝u_k+1。将参数u对时间t按泰勒公式展开，得到一阶逼近插值算法，其导数公式为^[121]

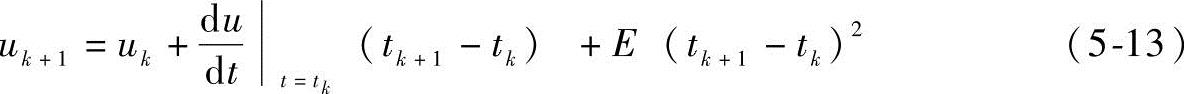
式中，E（t_k+1-t_k）2为一阶逼近误差。

插值周期为T_s，沿曲线的进给速度定义为

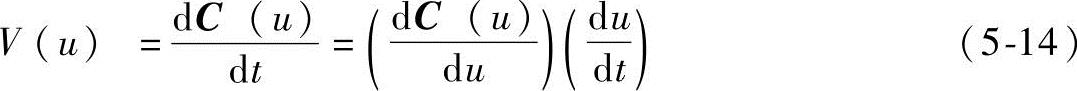
由于

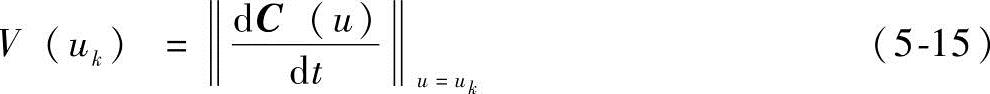
所以u对t的一阶导数可表示为

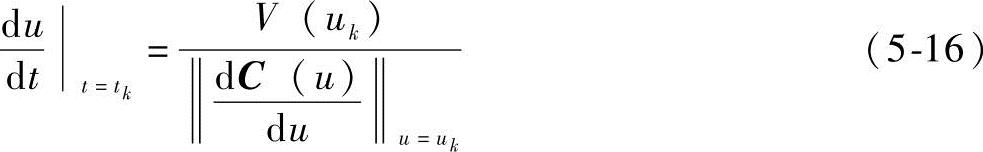
因此将式（5-16）代入式（5-13），忽略高阶项，由式（5-13）可得一阶插值算法

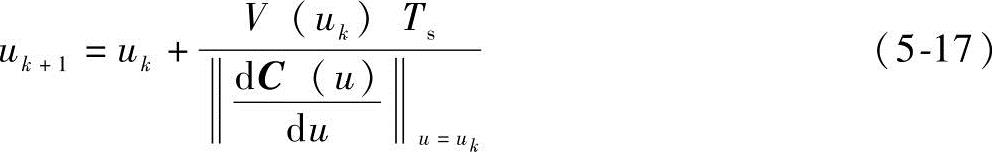
同样的，二阶插值算法为

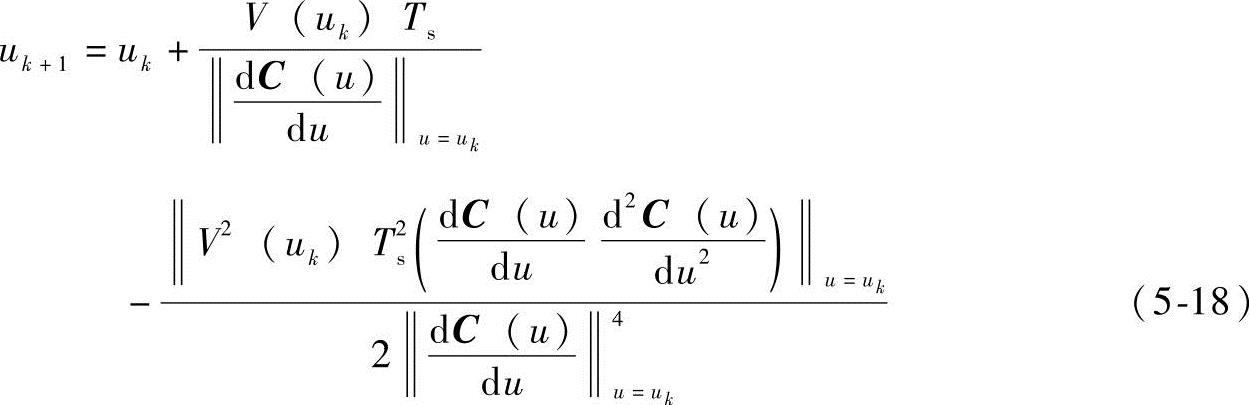
C（u）对u的一、二阶导数分别为

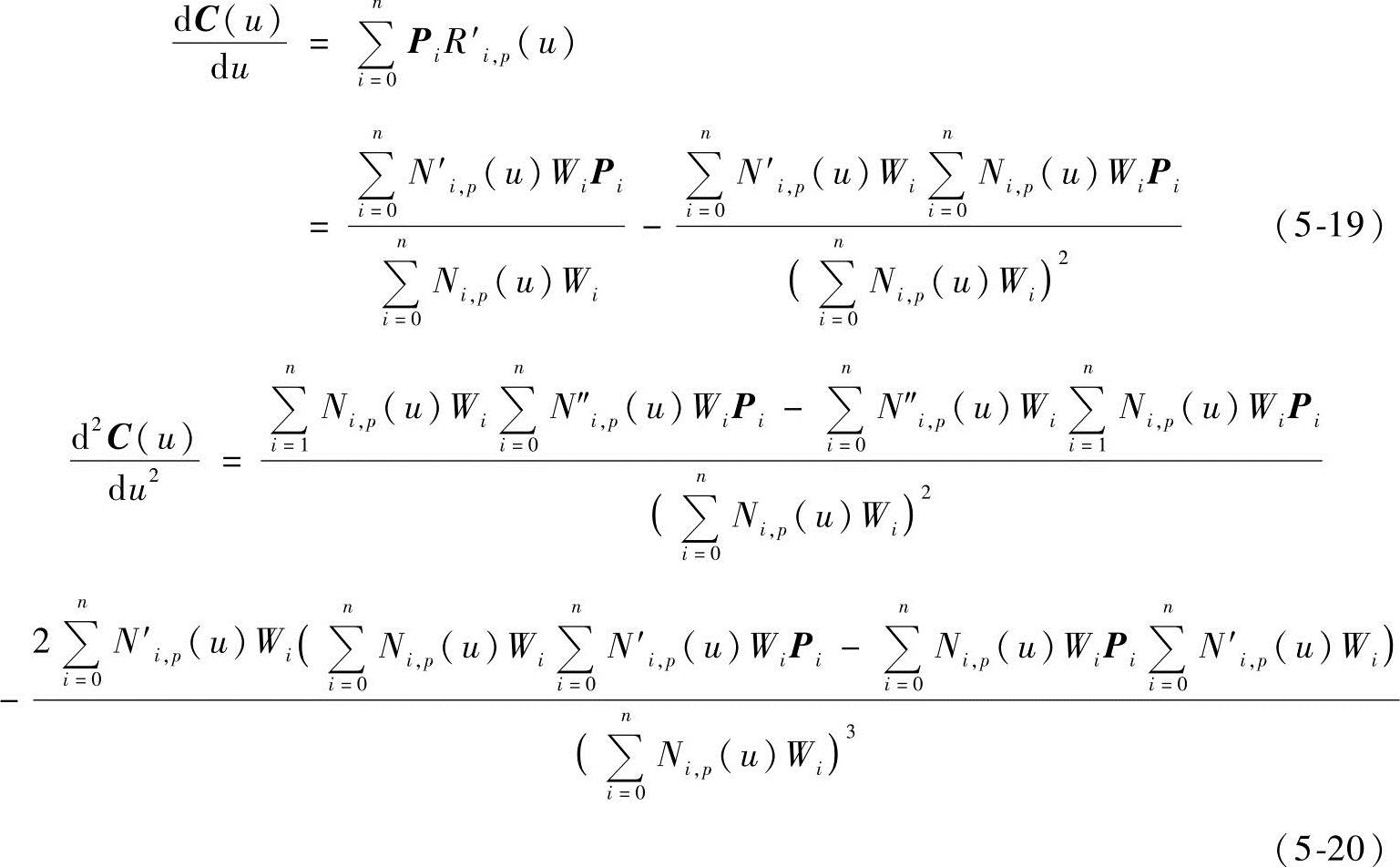
式中，N_i，P（u）的m阶导数通用计算公式为(www.daowen.com)

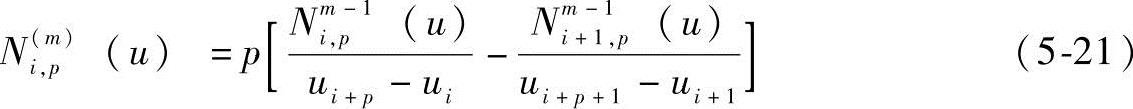
巨

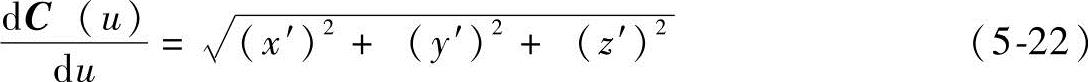
式中，

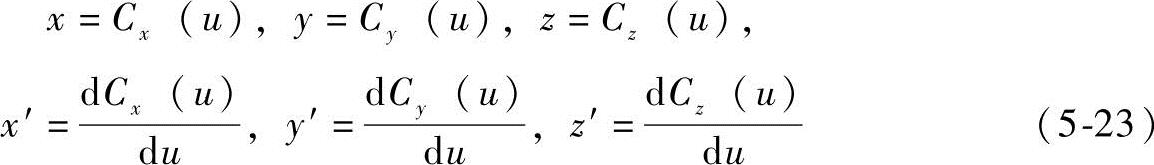
利用式（5-19）、式（5-20）、式（5-21）和式（5-23），可算出x′、y′、z′、x″、y″、z″。再利用算出的x′、y′、z′及式（5-17）、式（5-19）和式（5-22）可算出u_k+1，此即为一阶NURBS逼近插值算法；同样，二阶逼近算法是将算出的x′、y′、z′、x″、y″、z″代入式（5-18）、式（5-19）、式（5-20）和式（5-22）即可算出u_k+1。这样，在每个插值周期中，参数u按照给定的V（u_k）进行更新。然后利用式（5-23）算出目标位置。其中V（u_k）可以为给定的速度值，根据加减速算得的值或其他所期望的值。将得到的u＝u_k+1分别代入C（u）和C_T（u）就可以得到在t_k+1时刻刀心点C（u_k+1）和相应刀轴上的点C_T（u_k+1）。

假设刀轴单位矢量为T，则有

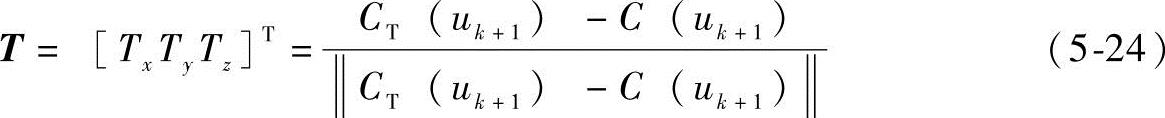
如图5-9所示，机床配置为工作台摆转立式5轴CNC机床。刀具随Z轴上下移动，摆动台和转动台绕工作台摆转支点P_S旋转指定的方位（B，C）。两个旋转角B和C可由式（5-25）确定：

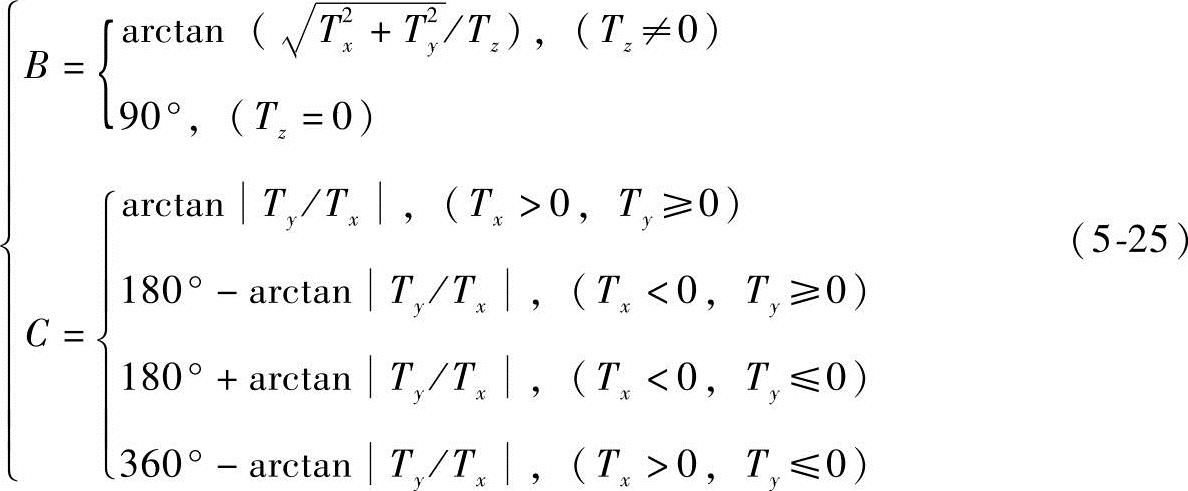
式（5-25）中，若T_x＝0，则arctan|T_y/T_x|＝90°。

（3）数据流的运动 从CAD/CAM中生成给定格式的双NURBS数控代码后，经译码器处理传给插值器；插值器根据给定的插值周期算出各轴运动目标值，再由Axis模块加载控制规律。

由于数控系统采用了SoftSER-CANS技术^[122]（国标IEC61491-SERCOS技术的软件实现，如图2-4所示），得到的数据被放入内部报文缓冲区（一块共享内存区），然后SoftSERCANS插卡与内部报文缓冲区交换数据（读写报文），接着Soft-SERCANS通过光纤环向各伺服驱动器发出包含运动指令的数据报文从而驱动电动机，整个过程如图5-10所示。

（4）实时性能测试 本书在一台主频为2.4GHz，内存512M的计算机上对给出的二阶近似五轴联动双NURBS插值算法进行了测试，结果如图5-11所示。

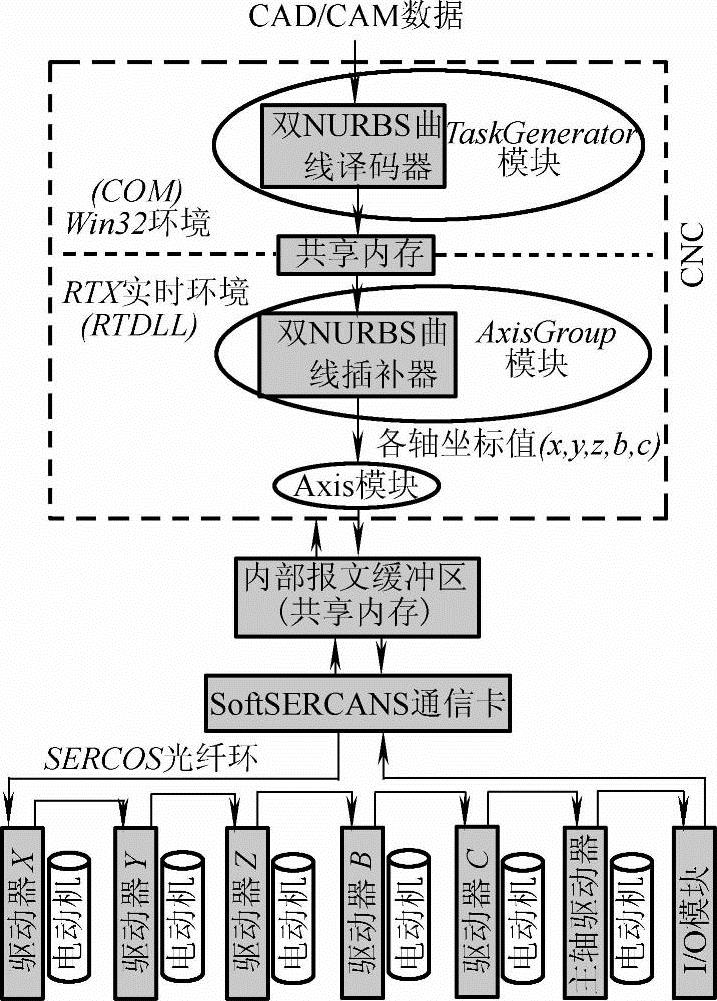
图5-10 数据流的运动

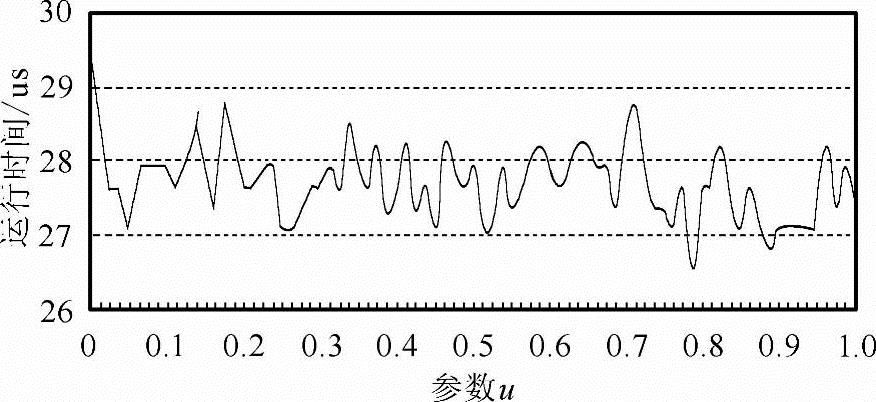
图5-11 给出方法的实时性能测试

各时间段的起始点为计算基函数的开始，终点为算出各轴的位置。从图5-11中可见，在一个双NURBS插值周期内，平均运行时间为28μs，该时间花销在插值周期为2ms甚至是500μs的数控系统中只占很小的一部分。

（5）加工误差分析 插值精度是评价一个插值方法好坏的重要指标。传统的线性插值程序段是在CAM阶段将曲线离散得到的，而本书提出的双NURBS样条插值方法是直接对曲线进行插值。虽然两者都以弦线逼近曲线，都存在弦高误差，但是由于本书方法逼近曲线的弦线为插值步长而线性程序段表示的线段通常为插值步长的好几偌，因此加工表面的精度较高。

对一段刀具轨迹分别采用双NURBS样条插值和传统的五轴线性插值方法，弦高误差在每个插值点处的曲率圆内计算得到，经采集数据可绘制出如图5-12所示的误差图。图中所示的刀具轨迹曲线拐点在参数值（节点矢量）u＝0.42附近，曲线曲率最小，其余地方曲率较大。从中可以看出，与传统线性段逼近曲线加工方式相比，本书的方法可以极大地改善加工性能，提高加工精度，而巨加工精度受曲线曲率变化的影响较小。

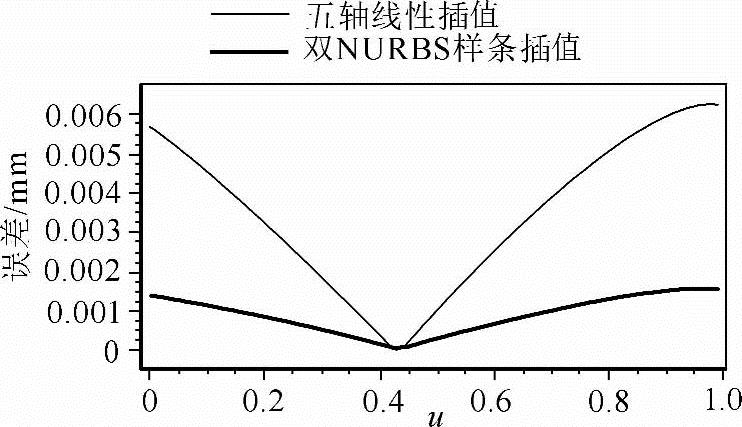
图5-12 两种方法的误差