前面讨论了单频连续波在理想条件下的声场。然而实际检测的往往是固体介质，且波源非均匀激发，辐射脉冲波声场，这样条件下的声场称为实际声场。那么实际声场与理想声场有哪些不同呢？通过图2-58来对实际声场和理想声场轴线上的声压做一个比较。

由图2-58可知，实际声场与理想声场在远场区轴线上声压的分布基本一致。

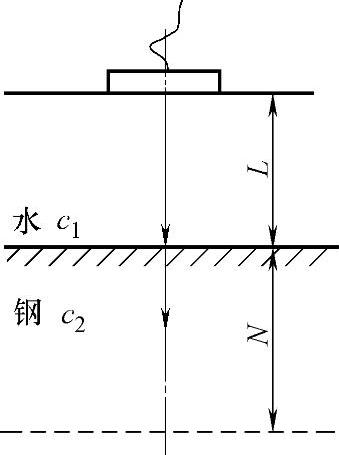
图2-57 近场在两种介质中的分布

但在近场区内，实际声场与理想声场存在明显区别。理想声场轴线上声压存在一系列极大值、极小值，且极大值为2P₀，极小值为零。实际声场轴线上声压虽然也存在极大值、极小值，但波动幅度很小，极大值远小于2P₀，极小值也远大于零，同时极值点的数量明显减少。这主要是因为理想声场为声波的干涉提供了良好的条件，在实际声场中则不能形成很好的干涉。而干涉的形成是近场出现极值点的前提。实际声场与理想声场对声波干涉的影响比较如下。

1）理想声场中的声波为单频连续波（即简谐诐），波源各点辐射的声波在声场中某点可能会产生完全干涉；而实际声场中的声波大多是脉冲波，脉冲波持续时间很短，波源各点辐射的声波在声场中某点产生不完全干涉或不产生干涉。且脉冲波含有多个频率分量，每个频率分量的波长不同，从而对应的近场长度、最大值点和最小值点的位置也不同，故各个频率分量的声压叠加后无明显的极大值、极小值点。由于脉冲波中其峰值频率对应的振幅最大，因此声压叠加时其权重也最大，故近场区内声轴线上的合成声压仍有一定的波动性。

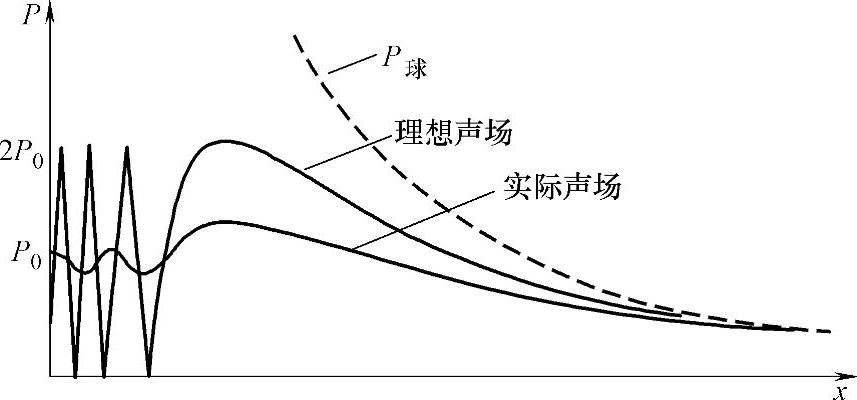
图2-58 理想声场与实际声场的声压比较(www.daowen.com)

实际声场在近场长度N附近存在扩散现象，例如使用K≥2.5，且晶片尺寸大于13mm×13mm的横波斜探头时，一般存在较严重的表面波，而此时声轴线对应的入射角明显小于第二临界角，这说明声束在斜楔（其声程一般小于近场长度）中已存在扩散现象，使得外侧声线的入射角大于或等于第二临界角。

这是由于实际声源含有多个频率分量，其中低于中心频率的分量对应的近场短、半扩散角大，故在X<N时就产生了扩散，因实际应用中近场长度N和半扩散角θ₀是以中心频率为基准计算得出的。

2）实际声场的波源是非均匀激发的，波源中心振幅大，边缘振幅小。由于波源边缘引起的波程差较大，对干涉影响也较大。因此这种非均匀激发的实际波源产生的干涉要小于均匀激发的理想波源。

3）前面讲过，理想声场是针对液体介质而言的，液体内某点的压强在各个方向上的大小是相同的，波源各点在液体中某点引起的声压可视为同方向而进行线性叠加。而实际检测对象往往是固体介质。在固体介质中，波源某点在固体中某点引起的声压方向在二者连线方向上。对于波源轴线上的点，由于对称性，使垂直于轴线方向的声压分量互相抵消，使轴线方向的声压分量互相叠加。很显然这种叠加干涉要小于液体介质中的线性叠加干涉。

以上三点都是实际声场近场区轴线上声压变化幅度远小于理想声场，极值点数量也明显减少的原因。

现代超声检测一般使用脉冲波，实验证明，若传声介质的衰减系数可忽略，则在近场区内，当接收换能器与活塞声源的尺寸相当时，其接收声压的平均值约等于P₀，且不随距离改变，这说明近场内的平均声压约等于平面波声压，这也是近场内的前几次大平底回波高度基本不变的原因。由于超声检测仪显示屏上的波高与接收声压成正比，而接收声压平均值与反射体的尺寸有关，实验证明，近场区内尺寸较小的平底孔回波声压与孔径平方成正比，例如可测得ϕ3.2mm、ϕ2mm、ϕ1.2mm平底孔回波比同距离处ϕ0.8mm平底孔回波分别高24dB、16dB和7dB，平均误差不超过±1dB。这说明在近场区内用对比试块法或距离-波幅曲线法确定缺陷当量有较高的准确度，或者说只要方法得当，近场区内的缺陷可以定量。这里需要指出的是，为提高用距离-波幅曲线法确定缺陷当量的准确度，用于绘制曲线的规则反射体的声程间距应尽量小，使曲线能反映近场区内声轴线上的声压波动特性（经典AVG曲线能看到上述波动特性）。