理想声场是指介质中超声波声压可以进行线性叠加，波源做活塞振动，辐射连续波等理想状态下的声场。液体介质中声压可以进行线性叠加，在研究理想声场时，常以超声波在液体介质中的传播为例。

1.圆盘源辐射的纵波声场

（1）声源轴线上的声压分布 在连续简谐纵波且不考虑介质衰减的条件下，图2-48所示的液体介质中圆盘源上一点波源d，辐射的球面波在波源轴线上Q点引起的声压为

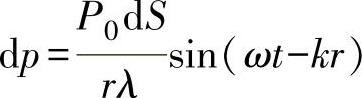
式中 P₀——波源引起的声压；

dS——点波源的面积；

λ——波长；

r——点波源至Q点的距离；

k——波数，k=ω/c=2π/λ；

ω——圆频率，ω=2πf；

t——时间。

根据波的叠加原理，做活塞振动的圆盘波源上各点波源在轴线上Q点引起的声压可以线性叠加，所以对整个波源面积进行积分就可以得到波源轴线上的任意一点声压为

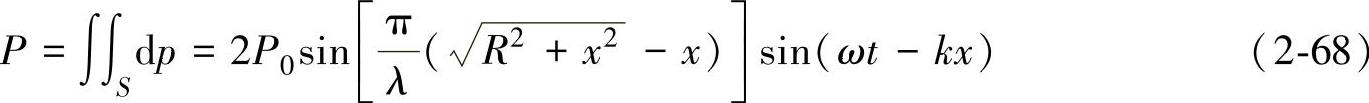
图2-48 圆盘声源的声压分布

其声压幅值为

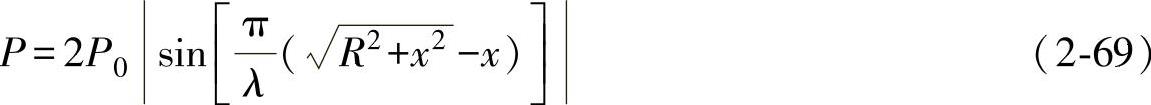
式中 R——波源半径；

x——轴线上Q点至波源的距离。

式（2-69）描述了声轴线上声压振幅随离开活塞中心的距离而变化的规律。式中P₀=ρcU为平面波声压幅值。

1）近场区。波源附近由于波的干涉而出现一系列声压极大值、极小值的区域，称为超声场的近场区，又称菲涅耳区。近场区声轴线上声压分布不均，是由于波源各点至轴线上某点的距离不同，存在波程差，互相叠加时存在相位差而互相干涉，使某些地方的声压互相加强，另一些地方互相减弱，于是就出现声压极大值、极小值的点。

波源轴线上最后一个声压极大值至波源的距离称为近场长度，用N表示。

当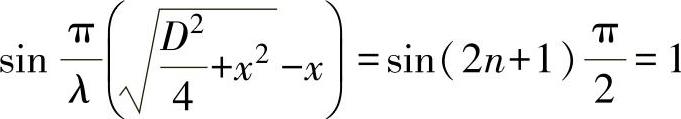时，声压P有极大值，化简的极大值对应的距离为

式中n=0，1，2，3，…<（D-λ）/（2λ）的正整数，共有n+1个极大值，其中n=0为最后一个极大值。因此近场长度为

当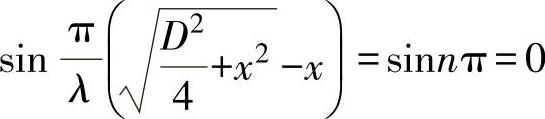时，声压P有极小值零，化简的极小值对应的距离为

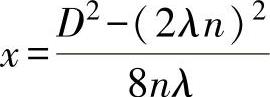
式中n=1，2，3，…<D/（2λ）的正整数，共有n个极小值，当n=1时，对应最远一个极小值点，若λ<<D，则此时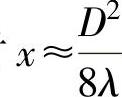，约等于N/2，即最远的最小值点约为近场长度的一半。

由式（2-71）可知，近场长度与波源面积成正比，与波长成反比。

由上面的分析可知，若超声检测使用简谐波，则在近场区检测定量是不准确的，处于声压极小值处的较大缺陷回波可能较低，而处于声压极大值处的较小缺陷回波可能较高，这样就容易引起误判，甚至漏检，因此如果用简谐波检测，则应尽可能避免在近场区检测定量。然而实际检测中都是使用脉冲波，从后面的分析可知，脉冲波的实际声场不同于简谐波声场。

2）远场区。x>>R称为远场区。当x>>R时，对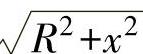做牛顿二项式展开并取前两项，可得

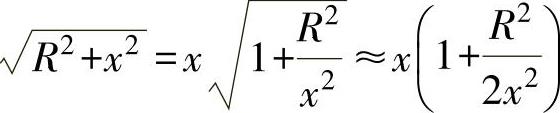
则式（2-69）中的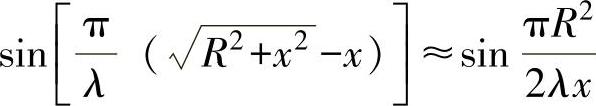，对此正弦函数做级数展开，并提取前两项可得

故x>N时，由式（2-69）和式（2-72）可得活塞源中心轴声压为

式中 F——活塞声源面积，F=πR²。取第一项，得

式（2-74）为远场声压公式，当x>N时，若用式（2-74）计算声压，其相对误差为

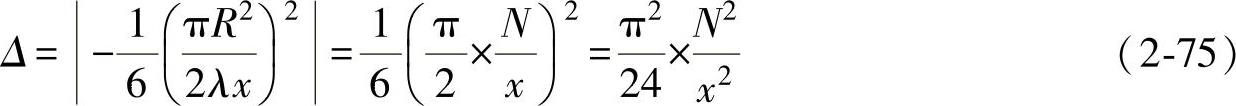
由式（2-75）可计算出，当x=1.67N时，Δ≈0.15。设此处球面波声压为1，则活塞源声压为0.85，用分贝值表示，此误差为1.4dB，记为Δ_dB=1.4dB。

同理，可求得：x=2N时，Δ=0.103，Δ_dB=0.9dB；x=3N时，Δ=0.046，Δ_dB=0.4dB；x=6N时，Δ=0.011，Δ_dB=0.1dB。

由上述计算结果可知，当距声源的距离x>3N时，用式（2-74）计算得出的声压的相对误差小于5%，误差分贝值小于0.4dB。

因此使用式（2-74）计算规则反射体回波声压或缺陷当量时，一般要求规则反射体或缺陷埋深大于3倍近场长度。不过，从上面列出的误差数据可见，利用式（2-74）计算规则反射体回波声压或缺陷当量时，x≥2N时误差可以接受，x≥3N时基本正确，x≥6N时误差可忽略不计。

活塞声源轴线上的声压随距离变化的情况如图2-49中实线所示，图中P_球表示球面波声压振幅的变化规律。

（2）远声场特性 式（2-74）是圆盘活塞源远场中声轴线上的声压表达式，远场中任意一点的声压如图2-50所示。

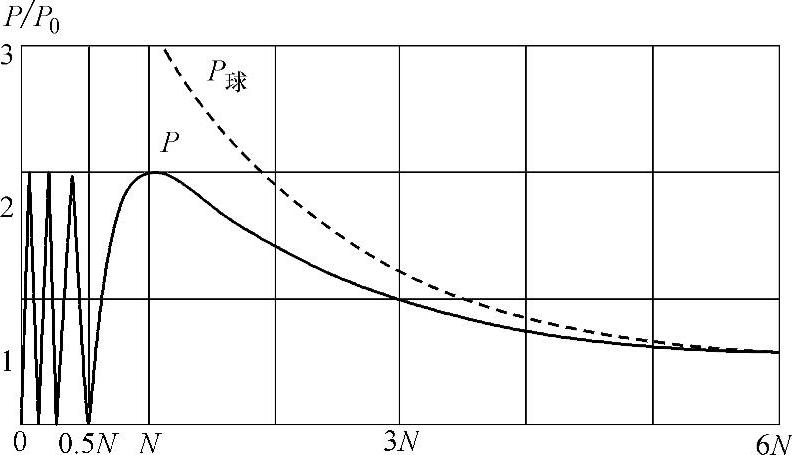
图2-49 圆盘源轴线上声压分布

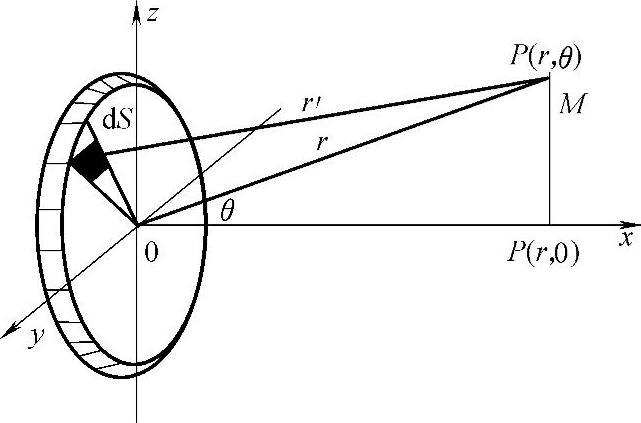
图2-50 远场中任意一点声压推导图

点波源dS在至波源距离充分远的任意一点M（r，θ）处引起的声压为

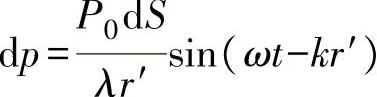
整个圆盘源在点M（r，θ）处引起的总声压为

式中 r——M（r，θ）点至波源中心的距离；

θ——r与波源轴线的夹角；

J₁——第一阶贝赛尔函数。

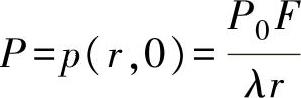由贝赛尔函数的性质可知，当Z=0时，，所以当θ=0°时，，故活塞源的指向性为

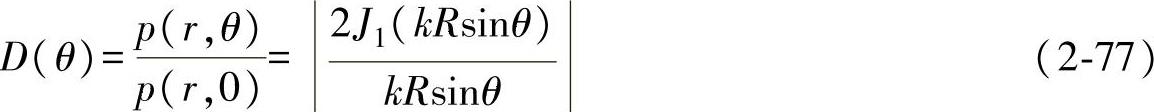
推导出式（2-76）和式（2-77）的前提是假设活塞源任一点dS到达M点的声压振幅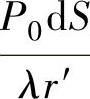中的r′可用r代替（图2-50），因此远场指向性和方向性函数必须在距离r>>R（晶片半径），即r′和r可近似看作平行线时才适用。

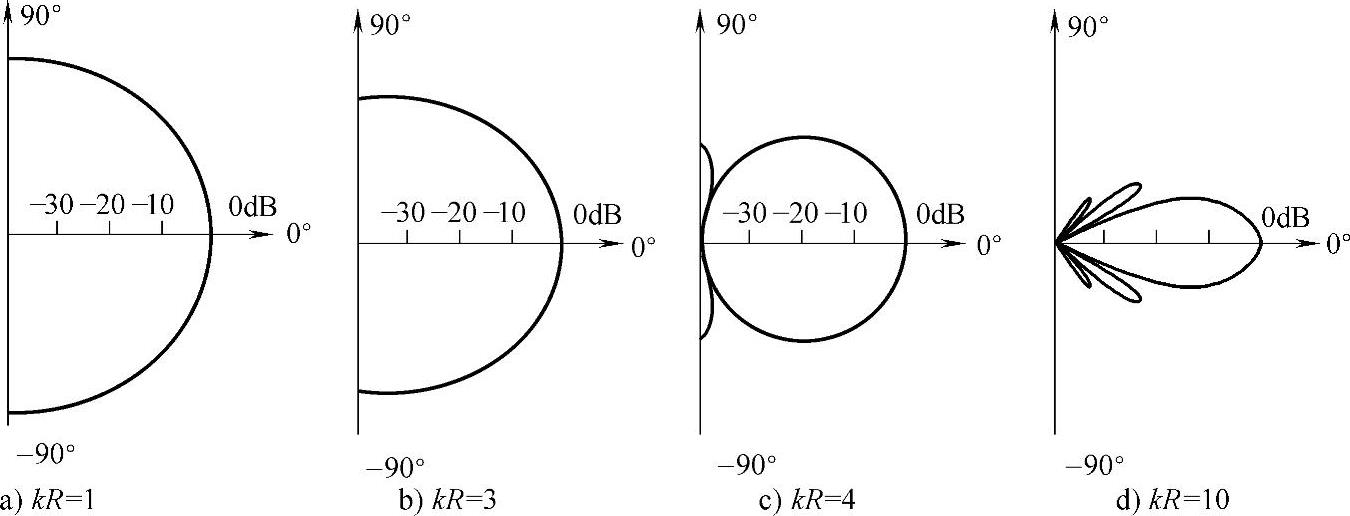
由式（2-77）可见，指向性与波数（k）和波源半径（R）的乘积有关。图2-51分别为kR=1、kR=3、kR=4及kR=10四种情况下，以分贝为单位的指向性图。当kR<1时，因为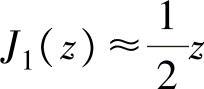，由式（2-77）得D（θ）≈1，也就是当活塞尺寸相对于介质中的波长较小时，辐射几乎是各向均匀的，这在图2-51中也得到反映，此时指向性图差不多是一个半球体。

随着kR值的增大，即随着活塞尺寸的加大或辐射频率的提高，指向性越来越尖锐。

当kR值超过一阶贝赛尔函数的第一个根值3.83以后，辐射开始具有更为复杂的指向性。例如在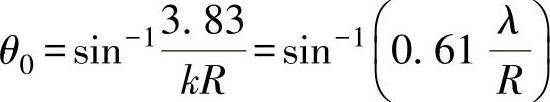的方向上D（θ）≈0，即辐射为零（图2-52）；超过这个角度，辐射又逐渐增加，并在某个角度达到次极大，此后再逐渐减小；从而在指向图上就表现为除主瓣以外还会出现一些副瓣，并当kRsinθ=3.83、7.02、10.2（相应于一阶贝赛尔函数的头三个极值）等数值时，D（θ）≈0，即在相应于这些值的θ角方向没有辐射。

(www.daowen.com)

图2-51 活塞源远场指向性图

然而，相对于主瓣而言，副瓣的辐射强度是很弱的，由J₁（x）曲线可以查得，图2-52中第一个次极大值约为0.14，因为能量正比于声压的平方，所以第一个副瓣的最大声强约为θ≈0°的主瓣声强的0.02倍。因此对于高频来说（kR值很大），辐射主要集中在θ=0的方向上，它形成了一个角度为2倍θ₀的锥形声束。其中

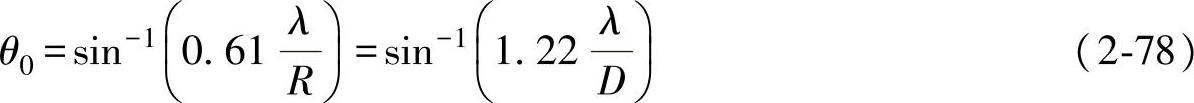
活塞尺寸越大，或者声源频率越高，则θ₀角越小，即指向性越强。在超声检测中，指向角是换能器的一个重要参数，θ₀越小，则对缺陷定位精度越高，横向分辨力越好。式（2-78）中D为活塞源直径。

应当注意，指向性是指远场而言，即要求r>>波源半径R，或r>>波源直径D。图2-52绘出了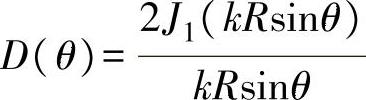随kRsinθ变化规律的曲线，由图可见，D（θ）对称于kRsinθ=0（即θ=0）的纵轴。即D（θ）或者说远场声束相对于θ=0有完全对称的分布，这从图2-51中可以得到印证。

金属材料检测中，kR值大多大于10，例如国内常用的直探头2.5P14Z，其频率为2.5MHz，压电晶片（即声源）直径为14mm，检测钢工件时，其kR值等于18.6，此时指向角θ₀约等于12°。当频率更高或压电晶片直径更大时，其kR值更大，θ₀角更小，指向性更好。

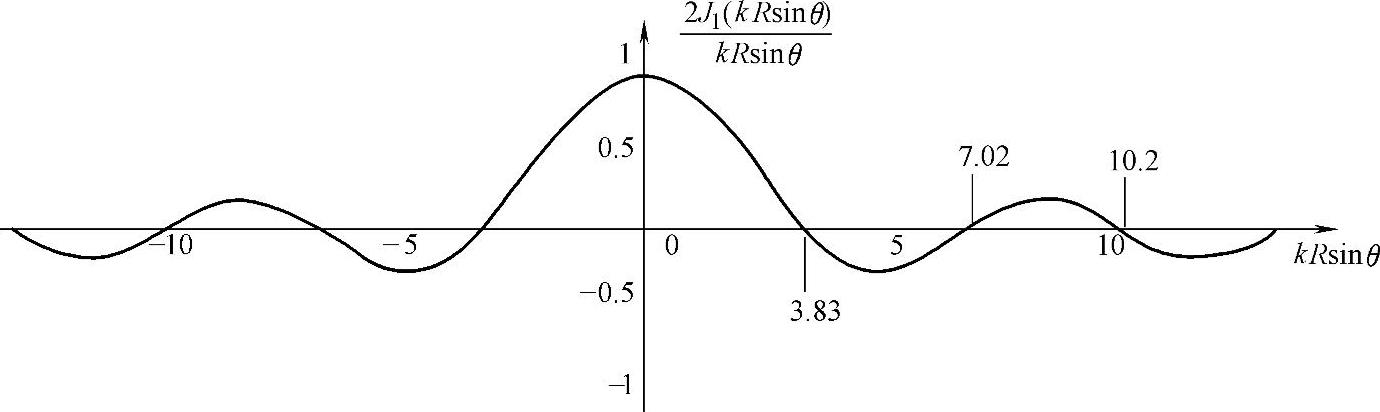
图2-52 圆盘源的指向性函数图解

为了着重说明kR>>1时声束在远场的指向特性，再重绘图2-51d，可得图2-53，即高频时远场声压随角度的变化关系。图中θ₀称为指向角，也称为第一零辐射角，2θ₀球面角对应声能的主辐射区，称为主声束，即主声束的宽度或球面扩散角为2θ₀，故θ₀也称为半扩散角。只有当缺陷位于主声束范围内时，才能被发现。

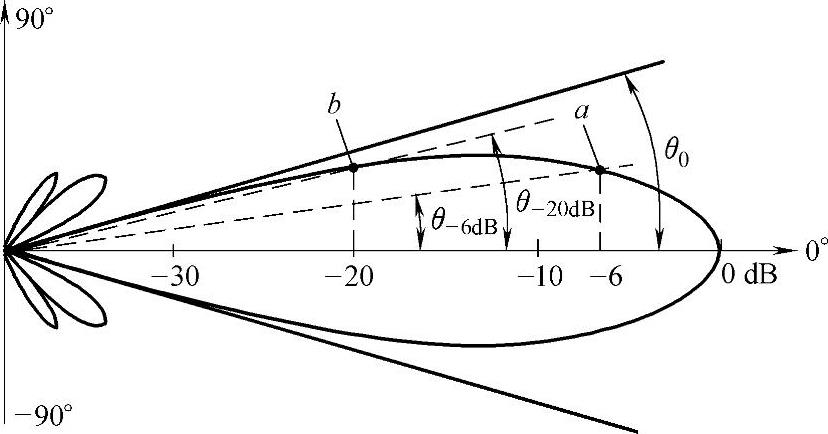
图2-53 圆盘声源远场指向性示意图

需着重指出以下几点：

①图2-53描述的是高频辐射时远场中与声轴线垂直的同一横截面上声压随角度的变化关系，图中纵坐标表示与声轴线的夹角；横坐标表示声压分贝值，以θ=0°（即声轴线上）声压为参考值0dB，θ>0°声压为负分贝，且θ越大，负分贝数也越大，直至θ₀时，辐射声压为零。图中曲线上的任一点对应该横截面上相关点的角度和声压参数。例如图中a点表示比声轴线声压低6dB的角度（记为θ_-6dB），b点表示比声轴线声压低20dB的角度（记为θ_-20dB）。

②主声束（也称主瓣）和副声束（也称副瓣）都是指远场中声压随角度的变化关系，绝不应认为副声束是靠近声源附近的声压分布，即绝不能把水平轴当成空间位移轴。

由于θ=θ₀处声压振幅为零，θ₀方向无法检测出缺陷，故有时也提到-20dB、-10dB、-6dB、-3dB时的辐射角，分别标记为θ_-20dB、θ_-10dB、θ_-6dB、θ_-3dB。

指向角是代表主声束范围的角度，反映了声束的定向集中程度及声束随距离扩散的快慢。指向角大小与声源的直径和波长相关。

当kR>>1，或者说波长λ<<D时，式（2-78）可简化为

θ₀≈1.22λ/D（弧度）=70λ/D（度） （2-79）

式（2-79）是介质中声波波长λ远小于活塞声源直径D时计算半扩散角的近似公式。由此式可见，当边缘辐射声压为零且角度以弧度为单位时，λ/D前面的系数为1.22。

下面分别给出λ<<D时，θ_-20dB、θ_-10dB、θ_-6dB、θ_-3dB所对应的半扩散角系数：

声压相对于声轴为-20dB时，系数为1.08，即：θ_-20dB≈1.08λ/D。

声压相对于声轴为-10dB时，系数为0.88，即：θ_-10dB≈0.88λ/D。

声压相对于声轴为-6dB时，系数为0.7，即：θ_-6dB≈0.7λ/D。

声压相对于声轴为-3dB时，系数为0.5，即：θ_-3dB≈0.5λ/D。

在常规超声检测中，半扩散角越小，则探头的指向性越好，声能越集中，检测灵敏度高，横向分辨力越好。

在主声束这个球面角内（即2θ₀内），当D_X=D，即X处的声束直径D_X等于声源直径D时，对应于θ_-6dB、θ_-20dB、θ0这三种情况：X与近场长度N的比值X/N分别约等于2.86、1.85、1.64，如图2-54所示。当X/N大于上述数值时，相应的声束直径将大于声源直径。但不能据此就说声束在X=2.86N或X=1.85N时才开始扩散，当然也不能说X=1.64N时才开始扩散，因为声束在X>N时已开始扩散。

由图2-49可见，当X>N时声轴线上的声圧是单调下降的，这种单调下降就是由扩散引起的。制作聚焦探头时，一般要求焦距F不大于近场长度N，否则聚焦效果变差[参见式（2-95）]，原因之一也是活塞源声束在X>N时开始扩散。

在反射法超声检测中，常用到回波声压相对于声轴线下降6dB和20dB的角度θ，此时λ/D前面的系数分别为0.50和0.88。即：θ_-6dB≈0.5λ/D，θ_-20dB≈0.88λ/D，单位为弧度。

声束在远场中随距离而扩散，即距离越远，声束直径越大。当λ<<D时，相对于θ_-6dB的情况，距声源X处的声束直径D_X≈Xλ/D；相对于θ_-20dB的情况，距声源X处的声束直径D_X≈1.76Xλ/D。

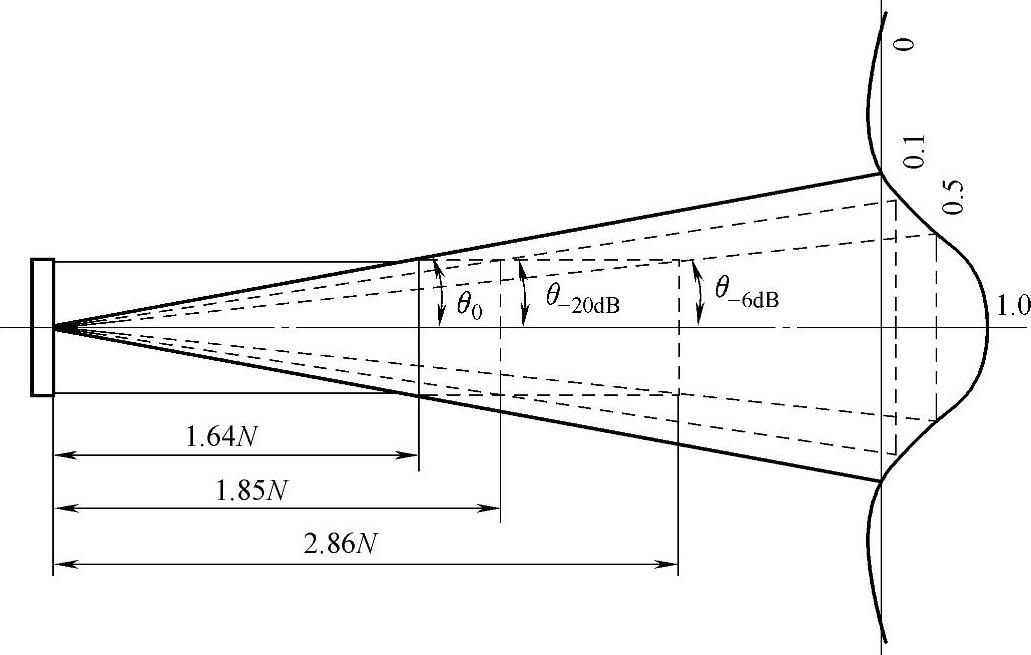
图2-54 圆盘源主声束内的扩散特性

当超声检测中使用频率较低或声源直径较小时，例如在铸钢件检测中可能使用1MHz频率的纵波探头，若此时的声源直径为6mm，则kR≈3，由图2-51 b可见，此时声束无明显指向性，也不存在声压为零的指向角和副瓣。

在衍射时差技术（Time of Flight Diffraction Technique，TOFD）等特殊检测方法中，希望声波有较大辐射区域，则希望指向性变钝，使部分波束沿近表面传播，部分波束经底面反射，部分波束在缺陷尖端产生衍射信号并根据这些信号到达接收探头的时差来确定缺陷的位置和自身高度。例如频率为3MHz直径为3mm的TOFD纵波探头，可计算得kR=4.8，半扩散角θ₀=58°，声束宽度对应的球面角=116°。

前面详细分析了圆盘源的声场特性。对金属材料检测而言，一般能满足kR≥10即高频辐射的条件，此时需着重关注的参数是近场长度N、声轴线上声压分布特性及半扩散角θ₀。由式（2-71）和式（2-79）可知，既要θ₀小又要N小是不可能的，当这两者不能兼顾时，一般是优先考虑指向性，因θ₀越小，则探头的指向性越好，声能越集中，检测灵敏度高，横向分辨力好。而对于近场长度N而言，实际声场在该区内的声压波动并不大，使用试块对比法仍可进行有效检测和定量。

2.矩形波源辐射的纵波声场

矩形波源辐射的理想纵波声场与圆盘源的情况基本相似。如图2-55所示，矩形波源做活塞振动时，在液体介质中辐射的纵波声场同样存在近场区和半扩散角。近场区内声压分布复杂，理论计算困难。远场区声源轴线上任意一点Q处的声压用液体介质中的声场理论可以导出，其计算公式为

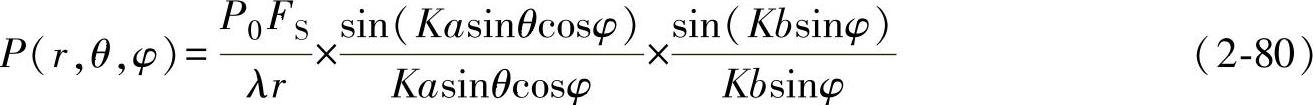
式中 F_S——矩形波源面积，F_S=4ab。

与圆盘源不同的是，矩形波源的声场不是旋转对称的圆锥形，而是矩形，如图2-56所示。当θ=φ=0时，由式（2-80）得远场轴线上某点的声压为

YOZ平面内半扩散角θ₀（单位：°）为

XOZ平面内的半扩散角θ₀（单位：°）为：

矩形波源在辐射方向即Z方向随θ、φ的变化有不同的指向角。以上只给出了矩形源两个边长方向的指向角。

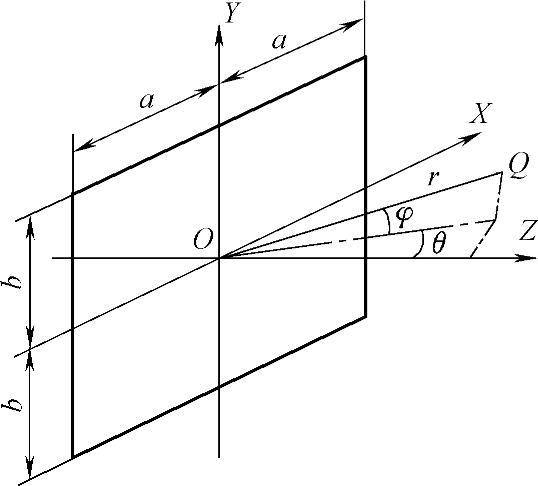
图2-55 矩形波源声场图

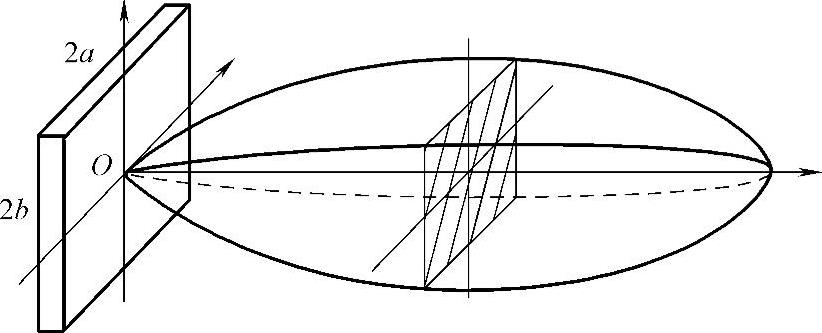
图2-56 矩形源波束指向

近场区即声压波动区，在此区域内存在声压极大值、极小值点。波源轴线上最后一个声压极大值至波源的距离称为近场长度，矩形波源的近场区长度与矩形的最长边有关，其值为

式中 L_max——矩形长边的长度。

工程上N可取长短边引起的波动区的几何平均值，此时

式中 L₁、L₂——矩形边长。

3.近场区在两种介质中的分布

前面给出的近场区长度的计算公式都只适用于近场区分布在同一介质中的情形。实际检测中，常会遇到近场区分布在两种不同的介质中的情况，例如水浸检测，超声波是先进入水，然后再进入钢中，如图2-57所示。当水层厚度较小时，近场区就会分布在水、钢两种介质中，此时水层厚度是可以人为控制的，即为已知量，要解决的是近场区在钢中的长度。

如图2-57所示，这种情况下，设介质Ⅰ（如上面所说的水层）的厚度为L，则介质Ⅱ（如上面所说的钢）中剩余近场区长度N为

式中 N₂——介质Ⅱ中近场长度；

c₁——介质Ⅰ中波速；

c₂——介质Ⅱ中波速；

λ₂——介质Ⅱ中波长。