1.波型转换

当声波倾斜入射到异质界面时，除了产生与入射波同类型的反射波和折射波以外，还会产生与入射波不同类型的反射波和折射波，例如，纵波斜入射，在入射角合适时，可能会反射和折射出纵波和横波。这种现象称为波型转换。波型转换现象只发生在斜入射的场合，而且与界面两侧介质的状态有关。

由于液体、气体介质中只能传播纵波，只有固体介质才能同时传播纵波和横波，因此波型转换只可能在固体中产生。同时还应指出，尽管气体介质理论上可以传播纵波，但由于气体特征声阻抗远小于固体或液体的特征声阻抗，使声波在固/气或液/气界面上产生全反射。因此可以认为声波难以从固体或液体中进入气体。

2.反射、折射定律

（1）纵波斜入射如图2-32a所示，纵波倾斜入射到异质界面时，反射波和折射波的传播方向（类似于光波一样）由反射、折射定律（又称斯涅尔定律）来确定，即

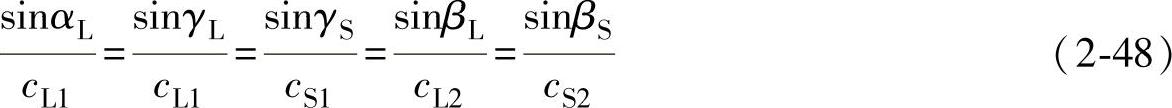
式中α_L——纵波入射角；

γ_L——纵波反射角；

γ_S——横波反射角；

βL——纵波折射角；

βS——横波折射角；

c_L1——第一介质中的纵波声速；

c_S1——第一介质中的横波声速；

c_L2——第二介质中的纵波声速；

c_S2——第二介质中的横波声速。

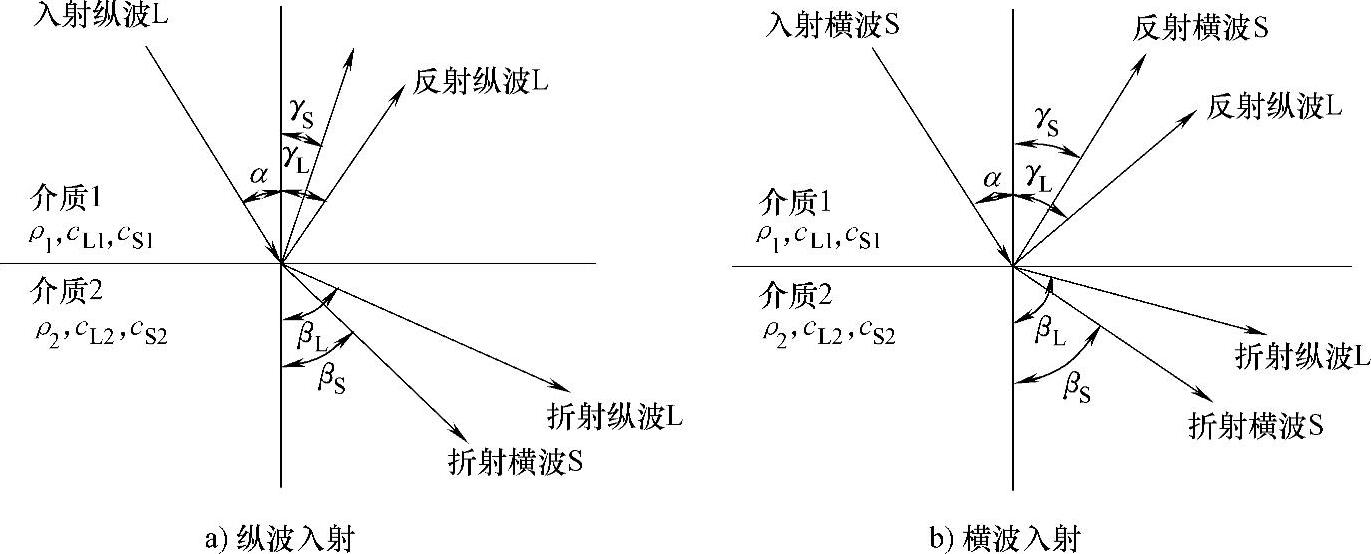
图2-32 声波倾斜入射

根据以上定律，由于同一介质中纵波声速不变，因此α_L=γ_L，即纵波反射角等于纵波入射角。又由于在同一介质中纵波声速大于横波声速，因此γ_L>γ_S，β_L>β_S，即纵波反射角大于横波反射角，纵波折射角大于横波折射角。

由式（2-48）可知，当第二种介质中的折射波型的声速比第一种介质中入射波型的声速大时，折射角大于入射角。此时，存在一个临界入射角度，在这个角度下，折射角等于90°，大于这一角度时，第二介质中不再有相应波型的折射波。临界角示意图如图2-33所示。(www.daowen.com)

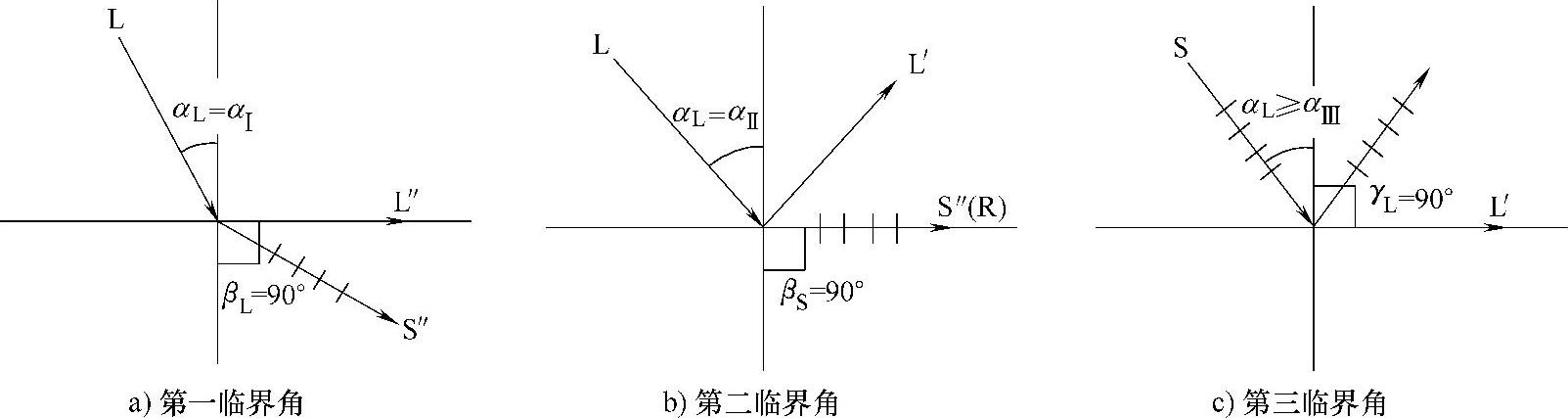
图2-33 临界角示意图

1）第一临界角αⅠ：由式（2-48）可以看出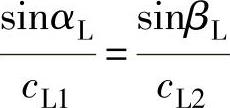，当c_L2>c_L1时，βL>αL，随着α_L增加，β_L也增加，当α_L增加到一定程度时，β_L=90°，这时所对应的纵波入射角称为第一临界角，用αⅠ表示，如图2-33a所示。此时。

2）第二临界角αⅡ：由式（2-48）可得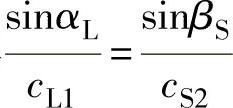，当c_S2>c_L1时，βS>αL，随着αL增加，β_S也增加，当α_L增加到一定程度时，β_S=90°，这时所对应的纵波入射角称为第二临界角，用αⅡ表示，如图2-33b所示。此时αⅡ=arcsin。

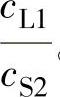由αⅠ和αⅡ的定义可知：

①当α_L<αⅠ时，第二介质中既有折射纵波L″又有折射横波S″。

②当αⅠ<α_L<αⅡ时，第二介质中只有折射横波S″，没有折射纵波L″。这是横波探头的制作原理。

③当α_L≥αⅡ时，第二介质中既无折射纵波L″，又无折射横波S″。这时在其介质的表面存在表面波，但此时的表面波不一定是瑞利波。

例如，纵波倾斜入射到有机玻璃/钢界面时。有机玻璃中：c_L1=2730m/s，钢中：c_L2=5900m/s，c_S2=3230m/s。则第一、二临界角分别为

由此可见有机玻璃横波探头27.6°<α_L<57.7°，有机玻璃表面波探头的激发角α_R=arcsin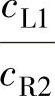，式中c_R2为工件中的瑞利波声速。因此用于钢制件表面波检测的探头：

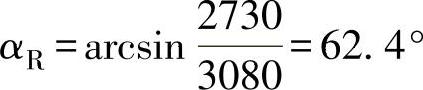
（2）横波斜入射当横波倾斜入射到固/固界面时，同样会产生波型转换，如图2-32b所示。各反射、折射波的方向符合反射、折射定律：

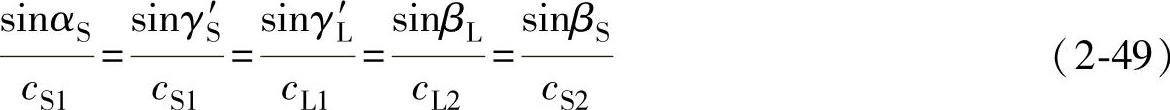
不难看出，横波倾斜入射时，同样存在第一、第二临界角，由于在实际检测中无多大实际意义，故这里不再讨论，这里只讨论第三临界角αⅢ。由式（2-49）可知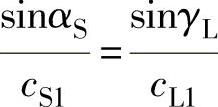，，随α_S增加，γ_L也增加，当α_S增加到一定程度时，γ_L=90°，这时所对应的横波入射角称为第三临界角，用αⅢ表示，，如图2-33c所示。当α_S≥αⅢ时，第一介质中只有反射横波，没有反射纵波，即横波全反射。对于钢：c_Ll=5900m/S，c_S1=3230m/s，则有

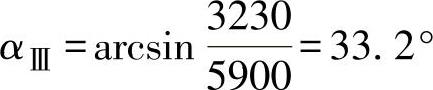
当α_S≥33.2°时，钢中横波全反射。