固体介质既能传播横波，又能传播纵波和表面波。前面已经讨论过，声波的速度与介质的弹性模量直接相关，超声波的波型不同时，由于对应弹性介质的弹性变形的形式不同，对应的弹性模量也不同，故同一介质中的横波、纵波和表面波的声速都不一样。

此外介质的尺寸对声速也有一定影响，下面就无限大固体、细棒及薄板介质中的声速进行分析讨论。

1.无限大固体介质中的声速

这里所讲的“无限大”是相对波长而言的。一般当介质尺寸远大于波长时，就可以视为无限大介质。声速的表达式可从波动方程推导而来，这里直接给出。

（1）无限大固体介质中的纵波声速cL

式中 E——介质的弹性模量；

σ——介质的泊松比，它是材料横向应变与纵向应变的比值的绝对值，也叫横向变形系数，是反映材料横向变形的弹性常数。其取值范围为0～0.5；

ρ——介质的密度。

（2）无限大固体介质中横波声速cS

式中 G——介质的剪切弹性模量。

（3）半无限大固体介质中表面波声速cR

由式（2-18）～式（2-20）可以得出以下结论：

①固体介质中的声速与介质的弹性模量和密度密切相关，不同的介质，声速不同；介质的弹性模量越大、密度越小，则声速越大。

②同一固体介质中，波型不同，则声速不同，且有下列关系：

c_L>c_S>cR

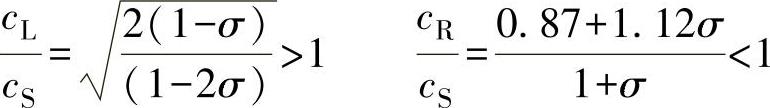
由公式可见，其速度比值只与泊松比有关。

2.细棒中的声速c_Lb

这里所讲的细棒是指直径与波长相当的棒类介质。声波在细棒中以纵波形式沿棒的轴向传播，又称棒波。棒波声速表达式为

(www.daowen.com)

常见固体的密度、声速和声阻抗见表2-2。

表2-2 常见固体的密度、声速和声阻抗

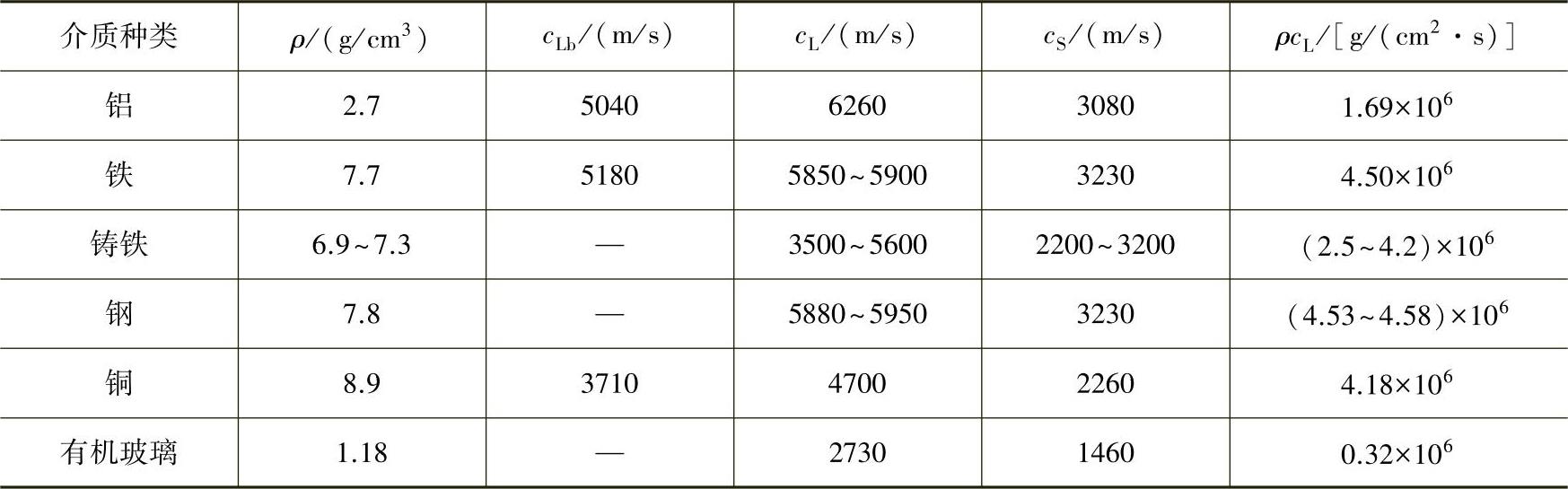
注：声阻抗的概念见2.5.2节。

3.板波（兰姆波）的声速

板波是在板厚与波长相当的薄板中传播的波。板波有对称型（S）与非对称型（A）之分。板波与横波、纵波、表面波不同的是，它的传播受到上下板面的影响，因此板波的波速不仅与介质性质有关，还与板厚、频率等有关。

板波声速有相速度和群速度之分。相速度是指单频波振动相位的传播速度，即单一频率谐波的传播速度。

脉冲波含有多个频率分量，每个频率分量在板中的传播速度不同。介质质点的振动是各个波振动的合成，合成振动形成的最大幅度的传播速度称为群速度，简言之，群速度就是脉冲波群最大幅值点的传播速度，也是脉冲波能量的传播速度。

无限介质中，群速度和相速度相同，即各频率分量的相位传播速度和脉冲波群的能量传播速度相同，故无限介质中的声速既是相位传播速度，也是能量传播速度。

板波声速公式推导比较复杂，这里直接给出关系式。板波相速度记为c_P，则对称型（S）有下列关系：

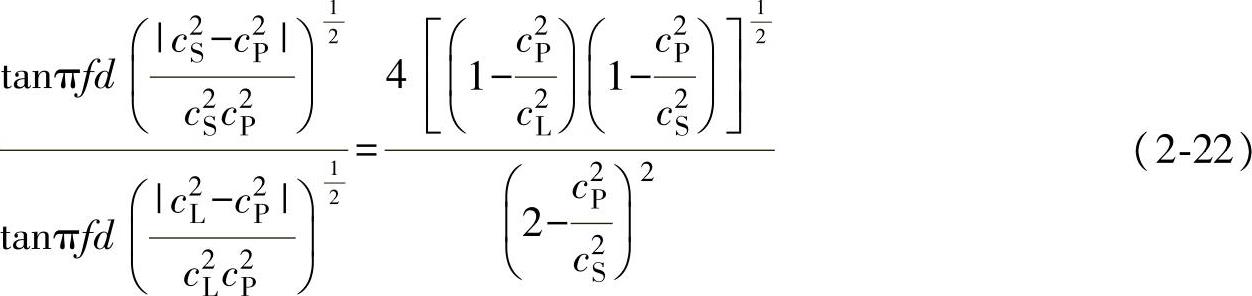
非对称型（A）有以下关系式：

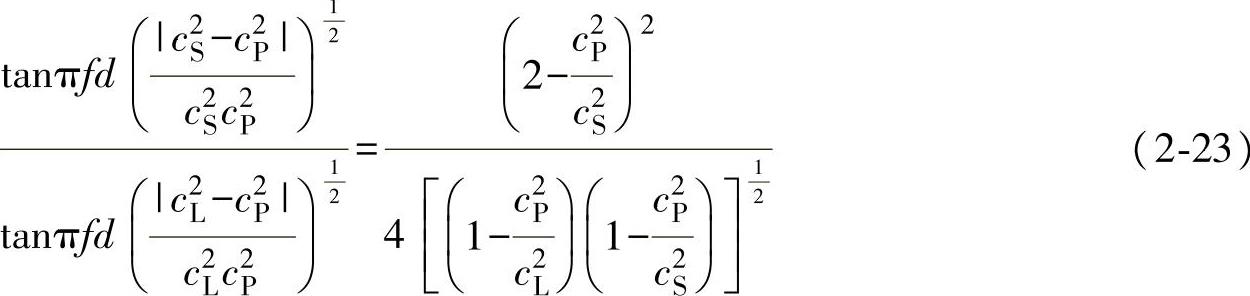
式中 c_P——板波相速度；

c_S——横波声速；

c_L——纵波声速。

由以上两式可知，板波声速c_P与fd、c_S、c_L有关。对于确定的介质，c_S、c_L为定值，因此对某一指定模式兰姆波而言，相速度仅是fd的函数。

兰姆波的相速度与群速度的求解计算量相当大，且十分复杂。一般通过查相应图表的方式来获得。图2-24和图2-25是相速度和群速度与fd的关系曲线图。图中S₀、S₁、S₂……表示不同模式的对称型兰姆波，A₀、A₁、A₂……表示不同模式的非对称型兰姆波。不同的fd、不同的兰姆波模式，将对应不同的兰姆波相速度和群速度。

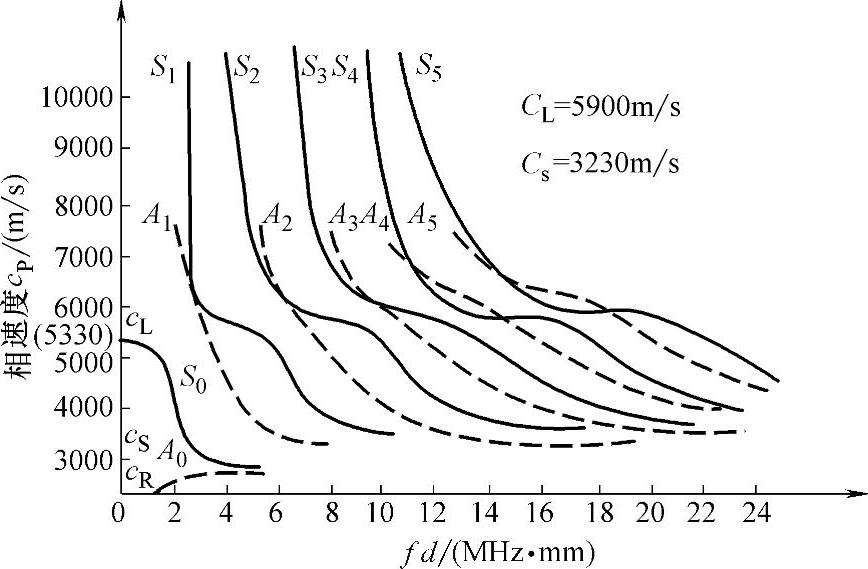
图2-24 钢板中兰姆波的相速度c_P与频率、板厚的关系

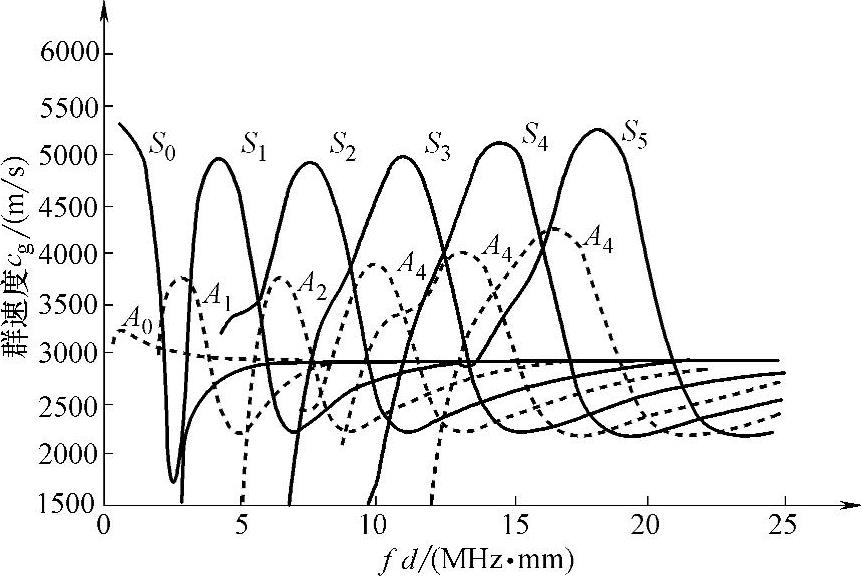
图2-25 钢板中兰姆波的群速度c_g与频率、板厚的关系