振动的传播过程称为波动。波动分为机械波和电磁波两大类。机械波是机械振动在弹性介质中的传播过程，如水波、可闻声波、超声波等。电磁波是交变电磁场在空间的传播过程，如无线电波、红外线、可见光、紫外线、X射线、γ射线等。

由于这里研究的超声波是机械波，因此下面只讨论机械波。

1.机械波的产生与传播

波动是一种重要而普遍的物质运动形式，机械振动在弹性媒质中的传播形成了机械波。下面通过两个简单的例子来理解波是怎么产生和传播的。

当向平静的水面投一小石子时，会看到水面上一圈圈起伏不平的波纹逐渐向四周传播出去，形成水波；用手握住绳子的一端上下抖动，就会看到凸凹相间的波向绳的另一端传播出去，形成绳波。

把介质想象成由无数个质点弹性地连接而成，如图2-5所示。由于相邻质点的力的作用，当介质中某一质点发生振动时，就会带动周围的质点振动起来，从而使振动向远处传播。

图2-6表示绳上一列波的形成过程。图中1～17各小点代表绳上的一排质点，质点间有弹力相联系。图中的第一行表示在开始时刻（t=0）各质点都处在平衡位置。其中第一个质点受到外力作用将开始在垂直方向上做简谐运动，设振动周期为T，则第二行表示经过T/4各质点的位置，这时质点1已达到最大位移，正开始向下运动；质点2的振动较质点1落后一些，仍向上运动；质点3更落后一些，此时振动刚传到质点4。第三行表示经过T/2后各质点的位置，这时质点1回到平衡位置，并继续向下运动，质点4刚到达最大位移处，此时振动传到质点7。依此类推，第四、五、六行分别表示了经过3T/4、T和5T/4后的各质点的位置，并分别显示了各个对应时刻所有质点所排列成的波形。

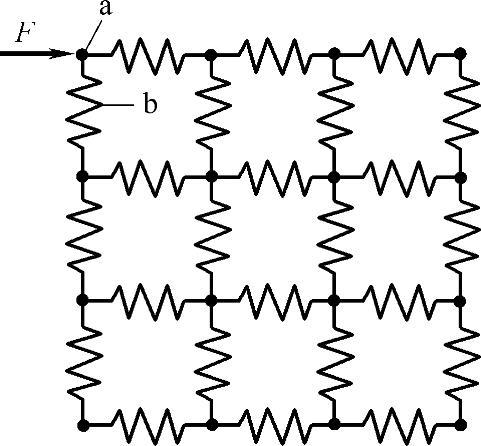
图2-5 弹性介质的模型

a—质点 b—表示弹性的弹簧

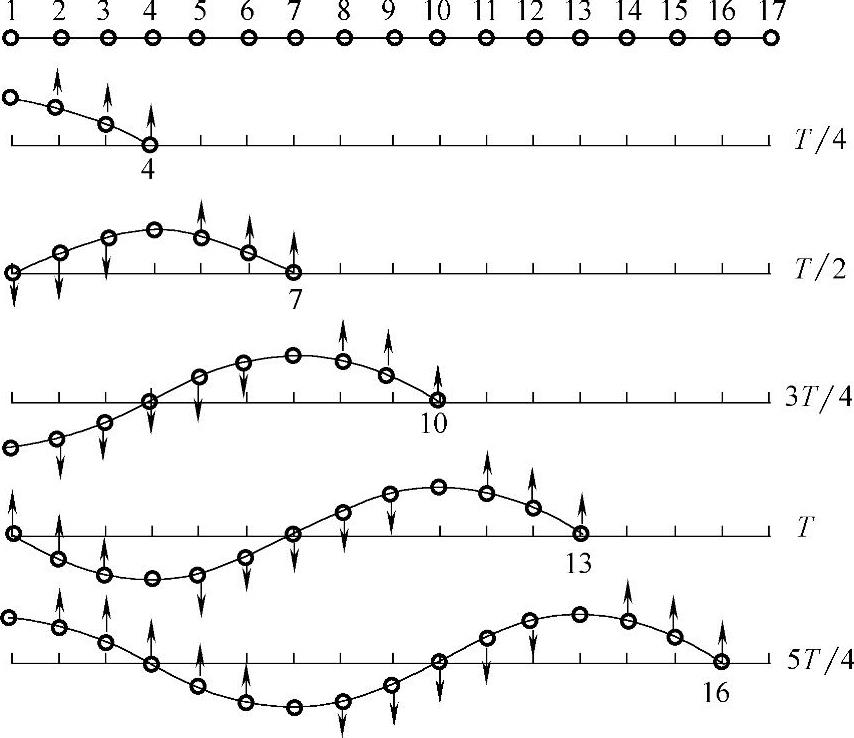
图2-6 各质点运动轨迹

由此，可以得出产生机械波的条件：一是有做机械振动的波源，二是存在能够传播机械振动的弹性介质。固体、液体、气体都可视为弹性介质。

机械波是构成介质的无数质点的一种共同运动形式；当介质发生振动时，各个质点在各自的平衡位置附近往复运动，质点本身并不随波迁移，机械波向外传播的只是机械振动的形式；另外机械波的传播过程还是振动能量的传播过程，这种能量是靠各质点的位移连续变化而逐渐传递出去的。

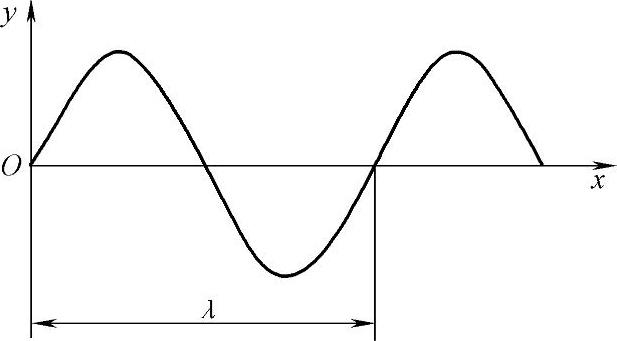
图2-7 波形图

2.描述机械波的物理量

（1）波长 波经历一个完整周期所传播的距离即为波长，用λ表示，如图2-7所示。沿着波的传播方向，在同一波线上相邻两振动相位相同的质点间的距离就等于一个波长。波长的大小由波源和介质共同决定。波长的法定计量单位为m，常用单位为mm。(www.daowen.com)

（2）频率（周期）单位时间内质点通过的完整波形个数就是频率，相应地通过一个完整波形所花的时间就是周期。频率用f表示，法定计量单位为Hz；周期用T表示，法定计量单位为s。周期和频率互为倒数关系。在一列波中，介质中各质点振动频率都相同，且等于波源的振动频率。波由一种介质进入另一种介质中传播时，波的频率是不改变的。

（3）波速 波动中，波在单位时间内所传播的距离称为波速，又称声速。它由介质的性质决定，与波源情况无关。波速用c表示，法定计量单位为m/s。

由波长、频率以及波速的定义可知，它们三者之间存在着如下关系：

c=λf 或因此在同一介质中，波长与波速成正比，与频率成反比。

3.由振动方程到波动方程

简谐振动在介质中传播形成简谐波。简谐波是最基本的波，是讨论其他复杂波动的基础。如图2-8所示，假设某一质点O在垂直方向y上做简谐振动，其振动形式沿x轴传播，形成一列简谐波，在此过程中，振幅A保持不变。O点的振动方程为

y₀=Acos（ωt+φ）

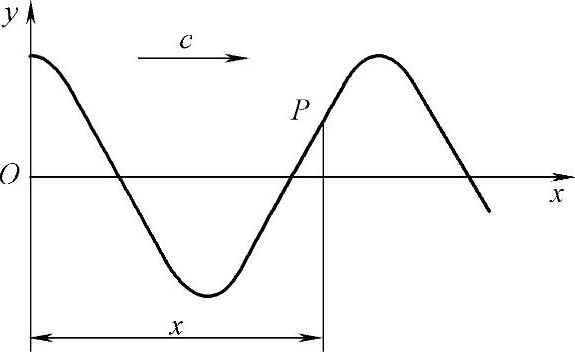
图2-8 简谐波示意图

对于波线上距波源O的距离为x的任意点P，其相位滞后于O点，在O点到P点范围内共有x/λ

个波，每个波对应的相位为2π，则P点滞后于O点的相位为2πx/λ。因此在任意时刻P点的相位为（ωt+φ-2πx/λ）。所以P点的振动方程为

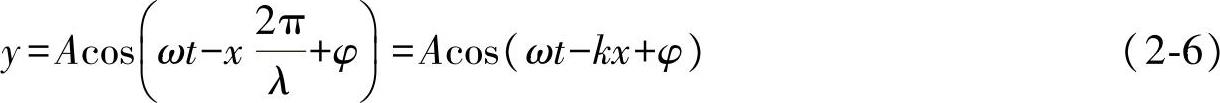
式中 k——波数，。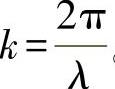

因为P点为波线上的任意点，式（2-6）反映了任意点在任意时刻的振动情况，因此它就是描写简谐波运动情况的波动方程（波函数）。

当波源处的初相位为0，即φ=0时，

y=Acos（ωt-kx） （2-7）这是平面简谐波最简单的波动方程，式（2-6）和式（2-7）中A为平面简谐波振幅。