1.机械振动的基本概念

物体或质点围绕其平衡位置所做的往复周期性运动称为机械振动，常简称为振动。如弹簧振子的运动；用线悬挂一小球，小球在竖直平面内的摆动（单摆）；击鼓后，鼓膜的起伏运动等。这些都是常见的机械振动，除此之外，一切能够发出声音的物体在发出声音时所做的运动以及超声波波源的运动等都是振动。我们之所以关心机械振动，正是因为超声波波源的运动也属于机械振动。

机械振动具有的特征：第一，平衡位置，即振动物体停止运动时所在的位置。例如，单摆的小球在平衡位置附近做周期性的左右摆动，经过多次重复，最终在平衡位置静止。第二，物体的运动具有往复性，这也是振动的最大特点。

产生机械振动必须具备的条件，一是每当物体离开平衡位置时就会受到回复力的作用，这也是振动物体的受力特征；二是阻力足够小，如果阻力大物体就无法振动，例如单摆的摆球在水中或在黏度很大的油里，由于阻力很大，几乎不会产生摆动。

2.与机械振动有关的物理概念

与机械振动有关的物理概念主要有全振动、回复力、振幅以及周期（频率）等。

（1）全振动 从某一振动状态出发，又回到该振动状态所发生的振动称为一次全振动。需要注意的是，振动状态是由振动位移的大小和方向、速度的大小和方向所决定的，只有当两个振动状态的位移（包括大小和方向）和速度（包括大小和方向）都相同时，这两个振动状态才相同。

（2）回复力 能够使振动物体回到平衡位置的力称为回复力。每当振动物体离开平衡位置就会受到回复力的作用。回复力是根据力的效果而命名的。它可以是重力、场力等各种性质的力，也可以是它们的分力或合力。例如在单摆中，回复力是重力的切向分量；而在弹簧振子中，回复力则是弹簧形变后产生的弹力。

（3）振幅 振幅是用来表示振动强弱的物理量，指振动物体离开平衡位置的最大距离，通常用符号A表示。简谐振动的振幅是不变的。强迫振动达到稳定状态时振幅也是一个常数。阻尼振动的振幅逐渐减小。

（4）周期与频率

1）周期：对于任何往复循环的物理过程，都用周期表示相应过程的快慢。当物体做往复运动时，完成一次全振动所需要的时间称为物体振动的周期，简称周，用T表示。周期的单位是秒。振动的显著特点是重复性，即周期性，就是振动物体的位移、速度、加速度经过一定时间之后又重复地回到原来的数值（即开始的状态）。周期这个物理量是物体运动周期性的描述。简谐振动是严格的周期性运动，它的周期是一个常数。有些振动（如阻尼振动）的周期在不断相对缓慢地变化。严格地说，这种往复运动已不再是周期性的，但周期这个物理量仍然可以反映这种运动的往复情况。

2）频率：振动物体在单位时间（通常是1s）内完成全振动的次数，称为频率，用f表示。国际单位为赫兹（Hz），1Hz表示1s内完成1次全振动，即1Hz=1次/s。此外，频率的常用单位还有千赫（kHz）、兆赫（MHz）等，它们之间的关系如下：

1kHz=10³ Hz 1MHz=10⁶ Hz

像周期一样，频率既可以表示振动或其他周期性运动的物体每秒钟完成周期性运动的次数，又可以表示某些物理量每秒完成周期性变化的次数。周期T等于频率f的倒数，即

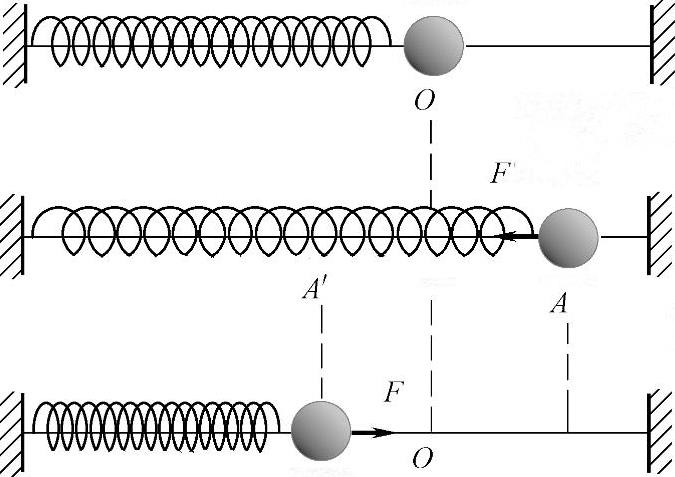
图2-1 弹簧振子的简谐振动

3.简谐振动

物体在受到大小跟位移成正比而方向恒相反的合外力作用下的运动，叫作简谐振动。下面通过弹簧振子系统来说明简谐振动的概念。图2-1所示为弹簧振子的简谐振动。其结构是由一个一端固定，质量可以忽略的轻弹簧和连在它另一端（自由端）的一个带孔而不易变形的小球m，并将小球m穿在一根光滑的水平杆上组成。

当小球处于O点时，所受外力的合力为零，弹簧没有变形，小球不受力，该点就是平衡位置。将小球从平衡位置O点向右拉到A点。然后释放，小球将沿杆左右振动。小球在振动过程中，它的重力和杆的支持力始终平衡。假定小球的运动没有其他任何阻力，对振动起作用的只有弹簧作用在小球上的弹力。当小球受外力作用被拉到A点时，相对平衡位置的位移方向向右，而弹力方向却向左；当小球运动到O点左侧时，位移方向向左，而弹力方向却向右，可见该弹力的方向总是跟小球对平衡位置的位移方向相反，即总是指向平衡位置，因此小球指向平衡位置运动时做加速运动，背向平衡位置运动时做减速运动，在平衡位置时速度最大，在最大位移点A时速度为零。显然这个弹力就是使小球振动的回复力。

物体（或质点）在受到与位移大小成正比，而方向总指向平衡位置的回复力作用下的振动，就叫作简谐振动。

振子m离开平衡位置的位移y与时间t的关系可用简谐振动方程来描述：

y=Acos（ωt+φ） （2-2）

式中 A——振幅，即最大水平位移；

ω——圆频率，ω=2πf；

φ——初始相位。

简谐振动的回复力总是和位移成正比，和位移方向相反，即F=-ky。振动物体的位移指振动物体相对于平衡位置的位移，因此简谐振动物体的位移是周期变化的。由F=-ky可知，简谐振动物体m受到的回复力和位移成正比，因此回复力也是周期变化的，且回复力的方向总是指向平衡位置。物体是否做简谐运动可以由回复力F=-ky的特点来判断。

从式（2-2）可知，能用余弦（或正弦）函数描述的振动称为简谐振动。

弹簧振子的运动规律如图2-2所示，图中以横轴表示时间t，纵轴表示质点位移y，则该图描述了振动质点的位移随时间变化的规律。(www.daowen.com)

式（2-2）描述的小球m的谐振动与做匀速圆周运动的质点M在y轴上的投影的运动特点完全一致。其方法是以小球m的位移振幅A为半径画圆，质点M沿圆周做匀速运动，如图2-3所示，则质点M在任意时刻t的水平位移y即可描述小球m的简谐振动规律。

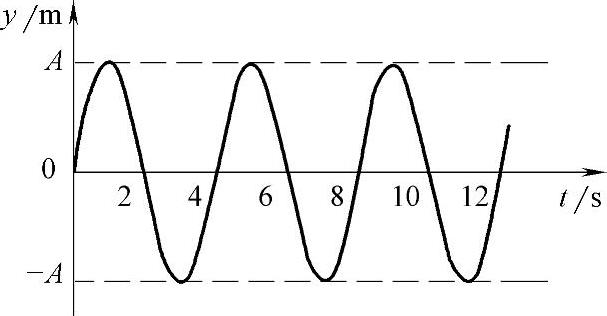
图2-2 简谐振动质点运动规律

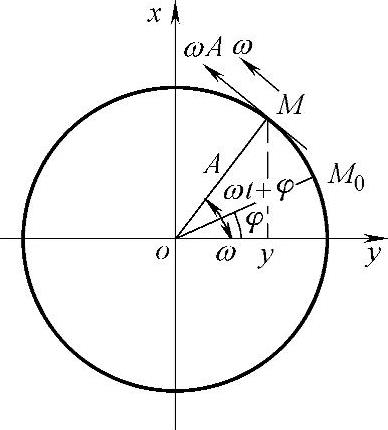
图2-3 质点M做简谐振动的等效图

小球m振动的加速度是由弹簧的回复力产生的。加速度的方向总是指向平衡位置。简谐振动物体的加速度是周期变化的，是变加速运动，在平衡位置加速度为零，在最大位移处加速度最大。简谐振动物体由最大位移处向平衡位置运动时做加速度减小的加速运动，再由平衡位置向最大位移处运动时做加速度增大的减速运动。

简谐振动物体的振动能量包括动能和势能，两者之和即总能量。总能量与振幅有关，随振幅的增大而增大。振动系统的动能和势能相互转化，在平衡位置动能最大、势能为零，在最大位移处势能最大、动能为零，但在任何位置其总能量不变。故简谐振动是机械能守恒的振动。

简谐振动是最简单最基本的振动。说它最简单是指没有任何其他振动能用单一的正弦或余弦函数描述，说它最基本是指任何其他振动都可分解为若干个或无限多个简谐振动之和。

4.阻尼振动

简谐振动是一种无阻尼振动，这是一种理想状况。实际上，任何振动物体都要受到阻力的作用。因受到阻力而使振幅不断减小的振动叫作阻尼振动。

振动的能量与振幅有关，因而阻尼振动就是能量不断减少的振动。能量减少的方式有两种：一种是由于摩擦阻力的作用使振动系统的能量逐渐转化为热运动的能量。例如单摆摆动的过程中振幅逐渐减小直至最终静止，就是由于空气的阻力作用使摆的机械能转化为空气的内能。另一种是振动系统引起周围物质的振动，使能量以波的形式向四周发出。例如：琴弦发出声音不仅因为有空气阻力要消耗能量，同时也因为以波的形式辐射而减少能量，最后琴弦会停止振动。因此阻尼振动有摩擦阻尼和辐射阻尼两种。

阻尼振动的振动方程为

y=A₀e^-βtcos（ω′t+φ） （2-3）

式中 y——位移；

β——阻尼系数；

ω′——阻尼振动圆频率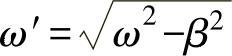，（ω为振动物体的固有频率）。

由以上阻尼振动方程可得位移-时间关系曲线，如图2-4所示。

5.受迫振动

振动系统在周期性的外力作用下发生的振动称为受迫振动或强迫振动，这个周期性的外力称为策动力或强迫力。比如扬声器纸盆的振动和耳机中膜片的振动都是因为受到外来策动力的持续作用而产生的。物体的受迫振动达到稳定状态时，其振动的频率与策动力频率相同，而与物体的固有频率无关。

做受迫振动的物体一方面克服阻力做功，输出能量，另一方面从策动力的做功中输入能量。当从策动力输入系统的能量等于物体克服阻力做功输出的能量时，系统的能量达到动态平衡，总量保持不变，振幅保持不变，做等幅振动。

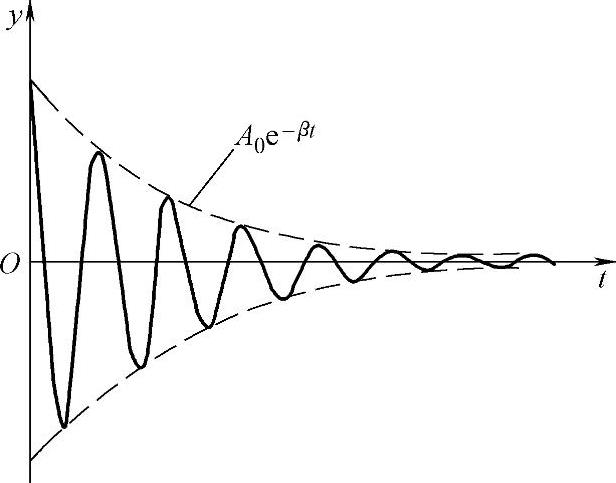
图2-4 阻尼振动位移-时间关系曲线

受迫振动的振动方程如下：

y=Acos（Ωt+φ） （2-4）

式中 A——受迫振动的振幅；

Ω——策动力圆频率；

φ——受迫振动的初相位。

当周期性策动力的频率Ω和物体的固有频率ω相等时振幅达到最大，即产生共振现象。共振在超声检测中也有应用，如超声检测中使用的探头。向工件辐射超声波时，其频谱中的最大幅值点的频率（峰值频率）就是探头的共振频率。