确定各种成形工序所需的成形力，是合理选用加工设备、正确设计模具和制订工艺规程的重要前提。求解塑性变形力时，需要确定变形体与工具的接触表面或变形区分界面上的应力分布，使得复杂的三维空间问题的解析非常困难。

塑性变形问题的完全解必须满足以下条件：

1.平衡微分方程

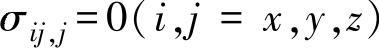
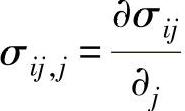其中，σ为应力张量， ，且 ，再根据x、y、z的方向得出三个平衡方程。

2.几何方程与体积不变条件

基于小变形的假设，应变ε_ij和位移u i的关系如下：

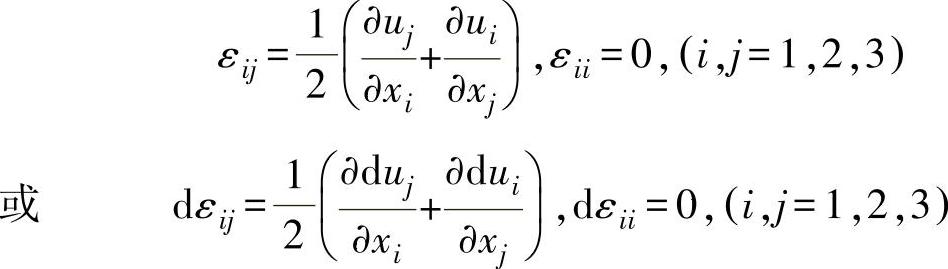
3.屈服准则

Von⁃Mises屈服准则：

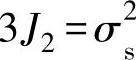
其中，

一点的主应力。4.边界条件（1）位移边界条件在S_u平面上：

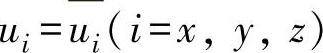
其中，在位移边界条件中，u i是由方程求解出的位移分量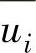， 是位移边界条件所已知的位移分量。

（2）应力边界条件(www.daowen.com)

在S_σ平面上：

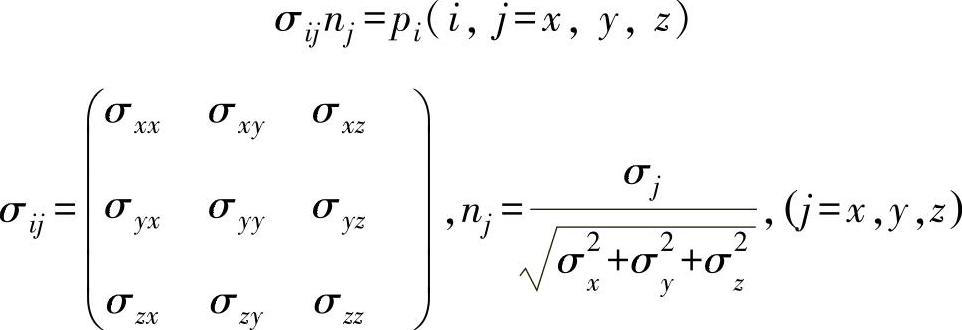
其中，在应力边界条件中，由方程所解出的应力应该等于外力p i。

一般而言，在塑性力学中的非线性问题很难求出解析解。但是，通过简化，利用极限分析法可以求得极限载荷的上限解或下限解。极限法是基于虚功原理与变分原理的，为了求得上限解，需要设定运动许可的速度场。根据上限法求得的载荷总会大于真实值，因此对设备和模具比较安全。对于可以作平面或子午面简化的塑性变形问题，利用上限法计算比较方便，但对于复杂问题，上限法难以应用。

有限元法（Finite Element Method，FEM）是一种分析金属成形过程的方法，以精度高、适应范围广和分析功能强等诸多优点成为最有效的方法。有限元模拟集成了塑性成形理论、成形工艺和计算机图形学，可以模拟整个锻造成形过程，比较准确地求解变形体内部的应力场、应变场、速度场、位移场等场变量，可以计算变形工序所需的成形力，同时也动态显示金属的变形过程，预测充填不饱满、折叠等工艺缺陷，从而为工艺分析提供科学的依据。根据其工作流程，有限元模拟系统可以分成图2⁃5所示的3个模块。

图2⁃5 FEM模拟流程^[7]

1.前处理

前处理是有限元模拟的基础，在整个系统中起着关键作用。前处理所需的数据包括模拟类型和参数、坯料和模具的几何模型、网格参数、工艺参数和边界条件等。此外，材料模型既可以从材料数据库中选择，也可以输入实验数据。对于热锻工艺的模拟，通常将材料模型定义为黏塑性。前处理的作用是为后续计算生成离散模型。

2.求解器

对用户来说，求解器就像是一个“黑盒子”，其功能是加载离散模型并转换为线性方程组，然后再逐步求解，计算数据将被保存到结果文件中。

3.后处理

后处理的功能就是用图形界面来显示和描述计算结果，将成形过程可视化，锻件应力、应变、温度和成形力等信息可以直接显示出来，让用户更直观地了解模拟结果。成形过程中材料流动趋势，可用流线图或速度矢量图来反映。对于锻造缺陷，如折叠和填充不足，也可以通过后处理来显示。图2⁃6所示为钟形壳锻件终锻成形的模拟结果与实际锻件的对比情况，右半部显示了锻件的流线分布与应变分布，流线连续合理分布，各区域的填充饱满，没有圆角过大或出现毛刺的情况。

图2⁃6 钟形壳锻造工艺模拟（图片来源：HATEBUR）