屈服强度是指使材料发生塑性变形的临界应力值。屈服准则（屈服面或屈服轨迹），是关于材料在各应力分量的组合作用下由弹性状态转变为塑性状态的一种假设前提。有两种常用的屈服准则：Tresca屈服准则和Von Mises屈服准则。

1.Tresca屈服准则其数学表达式为：

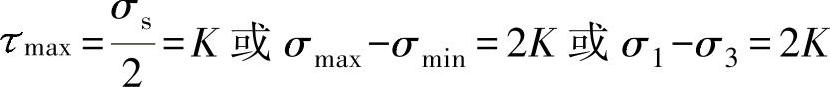
其中，σ_s为材料的屈服应力，max为最大切应力。从应力莫尔圆（图2⁃2）可以看出：σ₁和σ₃分别为最大和最小应力。

图2⁃2中给出了任意一点的一般应力状态，根据σ_x，σ_y，τ_xy，τ_yx的值按照τ_xy逆时针方向为正方向画出应力莫尔圆，并且从中找出最大切应力τ_max以及最大应力σ₁和最小应力σ₃。

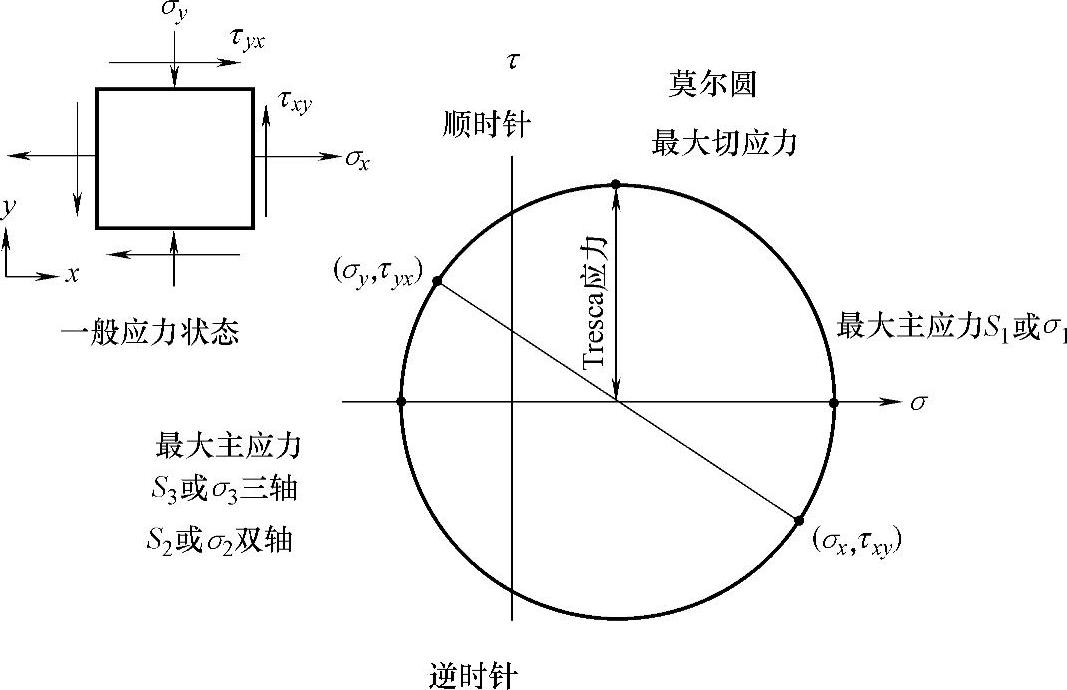
图2⁃2 应力莫尔圆^［4］(www.daowen.com)

根据Tresca屈服准则，当最大切应力达到临界值时，材料从弹性状态转变为塑性状态，与应力状态无关。由于Tresca屈服准则是线性的，当已知主应力大小和顺序时，使用该准则较简单。但通常主应力是未知的，使用Tresca屈服准则存在困难。

2.Von⁃Mises屈服准则

Von⁃Mises屈服准则是基于静水压力不能引起材料塑性屈服的结论。显然，仅畸变能影响材料从弹性到塑性状态的过渡。该准则可表述为：如果弹性变形能达到某个独立于应力状态的临界值时，材料从弹性状态转变为塑性状态。数学表达式为：

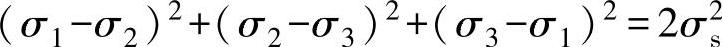
其中σ₁、σ₂、σ₃为主应力，σ₁≥σ₂≥σ₃，σ_s为屈服应力。

Von Mises屈服准则只有一个表达式，且在使用时不需要确定应力状态，因此比Tresca屈服准则更加方便实用。