1.二进制数

二进制数的1位（bit）只能取0和1这两个不同的值，可以用来表示开关量（或称数字量）的两种不同的状态，如触点的断开和接通、线圈的通电和断电等。如果该位为1，则表示梯形图中对应的位编程元件（例如位存储器M和过程映像输出Q）的线圈“通电”，常开触点接通，常闭触点断开，以后称该编程元件为1状态，或称该编程元件ON（接通）。如果该位为0，则对应的编程元件的线圈和触点的状态与上述的相反，称该编程元件为0状态，或称该编程元件OFF（断开）。在编程软件中，位编程元件的1状态和0状态用TRUE和FALSE来表示。

计算机和PLC内部用多位二进制数来表示数字，二进制数基数为2，遵循逢二进一的运算规则，从右往左的第n位（最低位为第0位）的权值为2n。

用位置记数法表示为

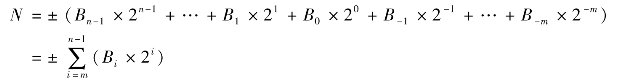
二进制常数以2#开始，可用下式计算2#1100对应的十进制数，即

2.十六进制

多位二进制数的书写和阅读并不方便。为了解决这—问题，可以用十六进制数来取代二进制数，二进制整数从最低位（小数从最高位）起，每四位用一位十六进制数表示，十六进制数的16个数字是0～9和A～F（对应于十进制数10～15）。B#16#、W#16#和DW#16#分别用来表示十六进制字节、字和双字常数，例如W#16#13AF。在数字后面加“H”也可以表示十六进制数，例如：

B3H=1011 0011B

1FB.02H=0001 1111 1011.0000 0010B

F3ADH=1111 0011 1010 1101B

3.数制转换

（1）十进制→二进制

整数部分：除基取余法——整数连续用基数2除，取各次余数，直到商为零。

小数部分：乘基取整法——小数连续乘基数2，每次取整数部分，直到小数为零；若小数乘2无法使尾数为零，则可根据精度要求求出足够位数。

例：分别将237和0.6875化为二进制数，其过程如下。

其结果是（237）10=（1110，1101）2，（0.6875）10=（0.1011）2(www.daowen.com)

（2）十进制→十六进制。

整数部分：除基取余法——整数连续用基数16除，取各次余数，直到商为零。

小数部分：乘基取整法——小数连续乘基数16，每次取整数部分，直到小数为零；若小数乘16无法使尾数为零，则可根据精度要求求出足够位数。

例：分别将237和0.5429化为十六进制数。

其结果是（237）10=（ED）16，（0.5429）10=（0.8AF）16，此时精度到小数点后三位。

（3）十六进制→十进制。

整数部分：按权展开法。

例：3D7BH=3×163+13×162+7×161+11×160

=3×4096+13×256+7×16+11×1

=12288+3328+112+11

=15739

小数部分：一般不用，使用时可化成二进制小数再做换算。

二进制→十进制：一般二进制先换成十六进制，再转换成十进制。

十进制→十六进制：一般十进制先转换成二进制，再转换成十六进制。

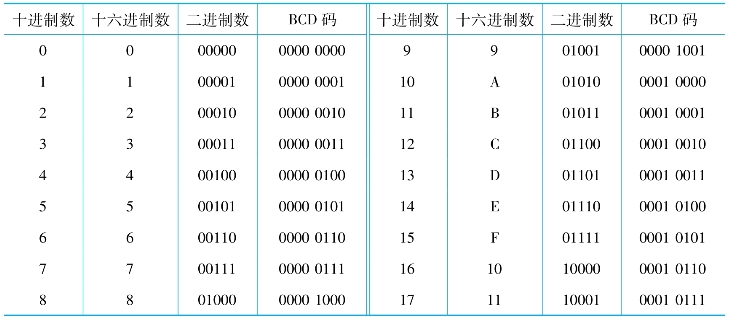
表5.1给出了不同进制数的表示方法，BCD码将在5.1.2节介绍。

表5.1　给出了不同进制数的表示方法