由于影响润湿的过程（如扩散、化学反应以及流动）具有多样性，并且可能会同时存在于一个系统中，因此描述这些过程的动力学的速度定律也不尽相同。这些速度定律与标准的流动控制的润湿模型不同。在化学和冶金反应中，当两个或更多的截然不同的过程同时起作用时，它们通常是以连续或平行的方式进行的。当涉及扩散、流动与反应的润湿过程被看作是连续过程时，这些过程中最慢的将成为控制因素。如果液体能够润湿裸露的基体，则润湿动力通常是由表面张力及黏度控制的。由流体流动控制条件下的金属液滴的润湿速率，比扩散与反应控制条件下的润湿速率要大得多。如果这三个过程同时存在于一个系统中，则流体流动可以忽略。在这种情况下，直至扩散物质与基体组元反应并生成产物时，液体才会润湿基体。液体从一种亚稳毛细状态向另一种亚稳毛细状态推进，并且在停止时仍可能处于亚稳的毛细状态。美国F.G.Yost提出反应润湿动力学模型建立在圆柱坐标系下，不考虑液滴的形状，并将扩散与反应的过程看成是一维的（沿径向）。初始条件（t＝0）为扩散（或反应）物浓度C（r，0）＝C₀。边界浓度，当r＝r（t）时为C_A，这里r为半径，r（t）为润湿边界的位置。润湿速率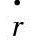为r（t）对时问的一阶导数。准平衡或缓慢流动的条件为：

式中D——液滴的扩散系数。

要使反应能够进行，润湿边界的浓度C_a必须比与基体达到化学平衡时的浓度C_e略大。扩散平衡方程的解满足如下条件：

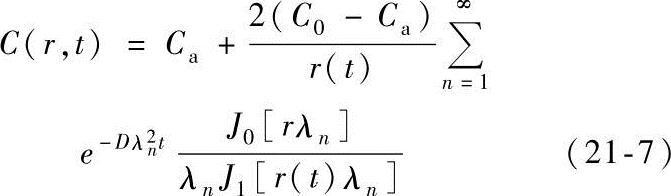
式中r（t）λ_n定义Bessel函数J₀的根。

润湿边界通量平衡服从下式：

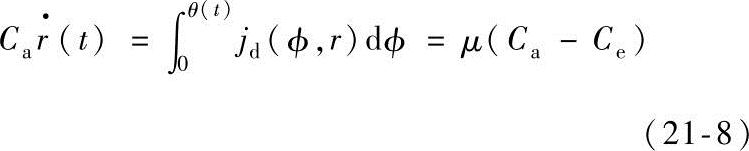
式中j_d（φ，r）——扩散通量，如图21-3所示。

μ——界面迁移系数，单位与速率单位相同；

θ——润湿角。

扩散通量可写成

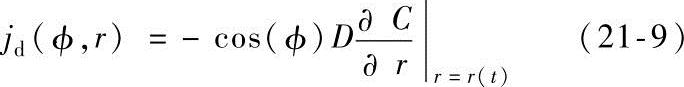
φ介于0到与基体的润湿角之问。

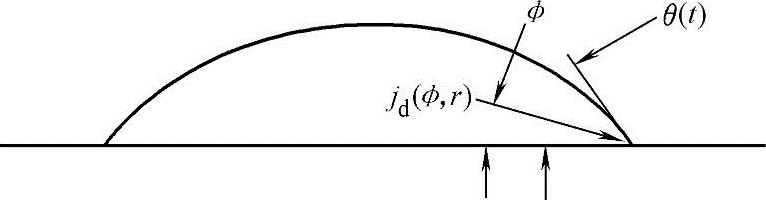(www.daowen.com)

图21-3 扩散通量示意图

扩散通量为φ的函数，总通量为函数j_d（φ，r）对φ从0到θ的积分。由式（21-8）和（21-9）得：

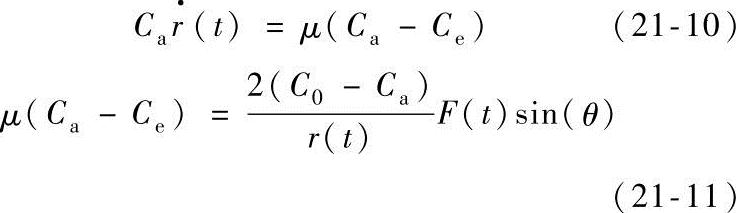
此处，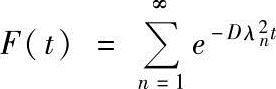

解方程（21-11）求得C_a，然后代入方程（21-10）得到润湿边界运动方程

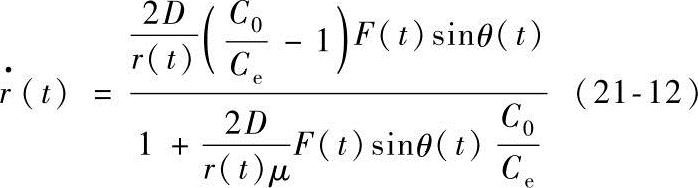
润湿角θ（t）可由初始液滴的体积求得。

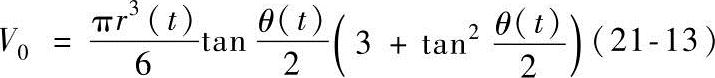
此时液体的体积保持不变，也就是说这里假设反应进行过程中消耗很少量的液体。从方程（21-12）可以看出，在反应控制条件下(即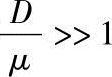＞＞1)，润湿速度为常数，且为

在扩散控制条件下(即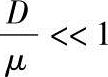＜＜1)，润湿速度为

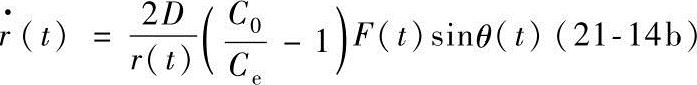
由式（21-14a）可以看出，反应控制是线性的，而在扩散控制条件下，其动力学方程由式（21-14b）给出。由于方程中含有F（t）和sinθ（t），故并非抛物线关系。

需要说明的是，反应润湿是一个复杂的过程，反应机制也是多方面的。例如，气氛也可能与基体反应，成为控制润湿动力学的一个方面。但是，将所有可能反应都包含在一个模型中是很困难的。