在研究讨论非正弦周期电流电路时，为了便于利用前面直流电路和正弦稳态电路的分析方法去分析非正弦周期电流电路，很有必要对非正弦周期信号进行分解，将非正弦周期函数分解为傅里叶级数。

对于给定的周期函数f（t），当其满足狄里赫利（Dirichlet）条件时，都可以分解为傅里叶级数。实际应用中常见信号通常都满足狄里赫利条件。

周期为T的时间函数f（t）可展开成

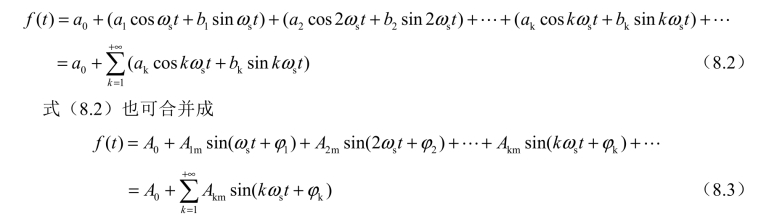
式（8.2）中，T为f（t）的周期；a0、ak、bk为傅里叶系数，其可按式（8.4）计算。

不难得出式（8.2）和式（8.3）中的系数有如下关系：

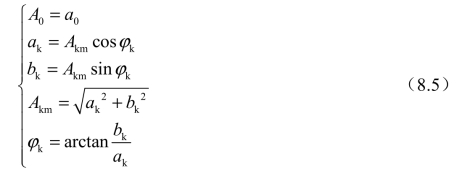
以上式（8.2）和式（8.3）的无穷三角级数称周期函数f（t）的傅里叶级数，式（8.3）中A0称为f（t）的直流分量。Akmsin（kωst+φk）称为f（t）的k次谐波分量。如：二次谐波（k=2），Akm称为k次谐波分量的振幅，φk称为k次谐波分量的初相角。特别地，当k=1时，A1msin（ωst+φ1）称为f（t）的基波分量，其周期或频率与f（t）相同。

将周期函数f（t）分解为直流分量、基波分量和一系列不同频率的各次谐波分量之和，称为谐波分析。根据式（8.3）和式（8.4），再利用式（8.5）很容易得到式（8.2）形式的f（t）的傅里叶级数。表8.1给出了几种常见的非正弦周期函数的傅里叶级数形式。

由于非正弦周期函数f（t）在分解为傅里叶级数时，f（t）波形的某种对称性与傅里叶级数有着密切的关系。因此，在对非正弦周期函数f（t）进行傅里叶分解时，根据f（t）波形的特点可使系数a0、ak、bk的确定简化，大大方便了傅里叶级数的计算。下面讨论几种常见的对称波形。

1.周期函数为偶函数

如图8-7所示的函数波形对称于纵轴，在数学上称为偶函数。其满足

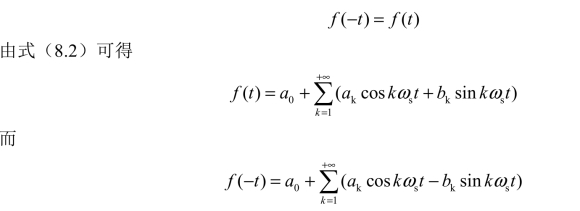
由于f（-t）=f（t），故得bk=0。

由此可知，关于纵轴对称的偶函数的傅里叶级数中不含正弦谐波分量，即

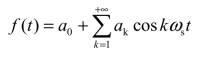
2.周期函数为奇函数

如图8-8所示的函数波形对称于原点，在数学上称为奇函数。其满足

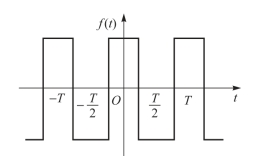
图8-7　偶函数波形

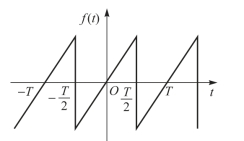
图8-8　奇函数波形

由式（8.2）可得

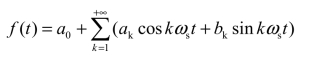
而

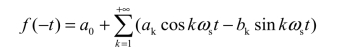(www.daowen.com)

由于f（-t）=-f（t），故得a0=ak=0。

由此可知，关于原点对称的奇函数的傅里叶级数中不含直流分量和余弦谐波分量，即

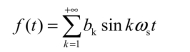
3.周期函数为偶谐波函数

图8-9所示的函数波形，两个相差半个周期的函数值大小相等，符号相同，在数学上称为偶谐波函数。其满足

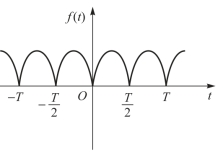
图8-9　偶谐波函数波形

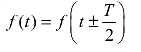
由式（8.2）可得

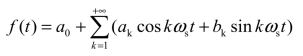
而

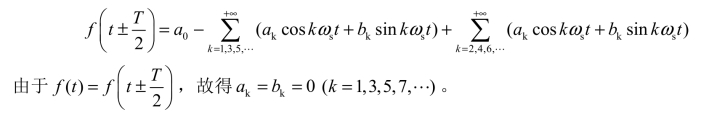
由此可知，偶谐波函数的傅里叶级数中只含直流分量和各偶次谐波分量，故称偶谐波函数。即

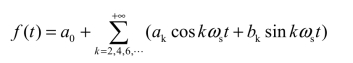
4.周期函数为奇谐波函数

如图8-10所示的函数波形，两个相差半个周期的函数值大小相等，符号相反，在数学上称为奇谐波函数。其满足

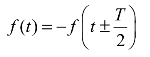
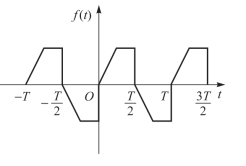
图8-10　奇谐波函数波形

由式（8.2）可得

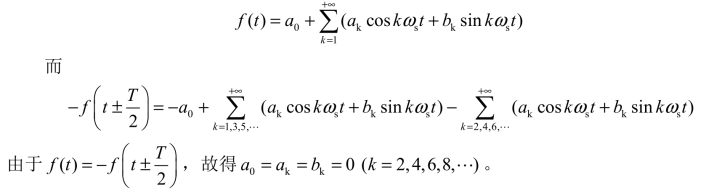
由此可知，奇谐波函数的傅里叶级数中只含各奇次谐波分量，故称奇谐波函数。即

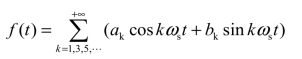
综上所述，根据周期函数的对称性不仅可预先判断它包含的谐波分量的类型，定性地判定哪些谐波分量不存在，并且使傅里叶系数的计算得到简化。

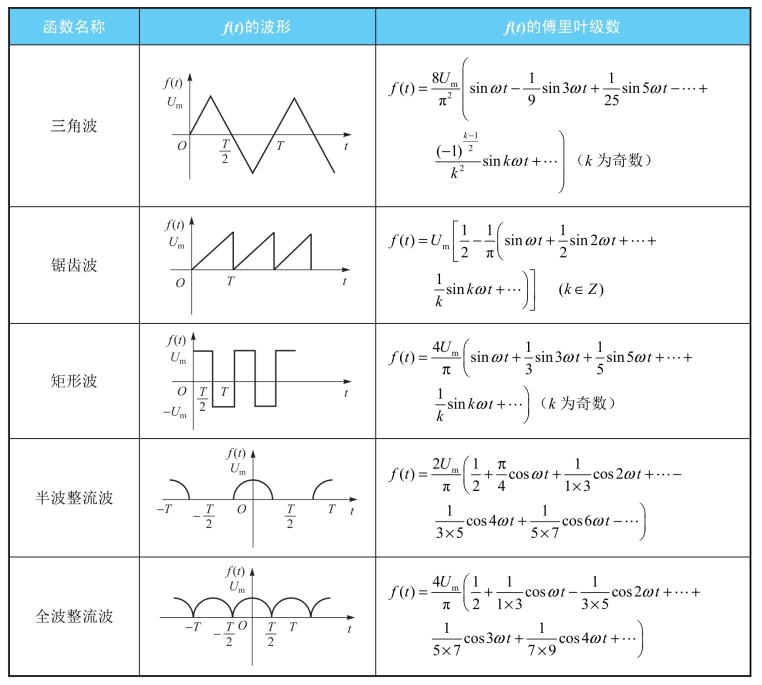
实际应用中，常通过查表8-1直接写出周期函数的傅里叶级数形式。

表8-1　几种常见的非正弦周期函数的傅里叶级数形式