串联谐振电路的谐振曲线

如图6-3所示串联谐振电路，当电压源的频率变化时，电路中的电流、电压、阻抗都将随频率变化而变化，这种随频率变化的关系称为频率特性。其中表明电流、电压与频率关系的曲线称为谐振曲线。

1.频率特性曲线

如图6-3所示串联谐振电路，它的复阻抗为

它的幅频特性和相频特性分别为

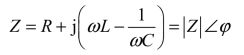
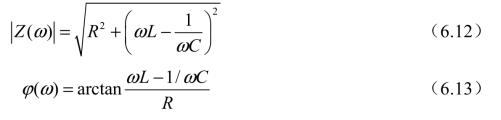
相应的幅频特性曲线和相频特性曲线如图6-4所示。

由图6-4可以看出，当ω=ω0时，阻抗为纯电阻且阻抗值最小。

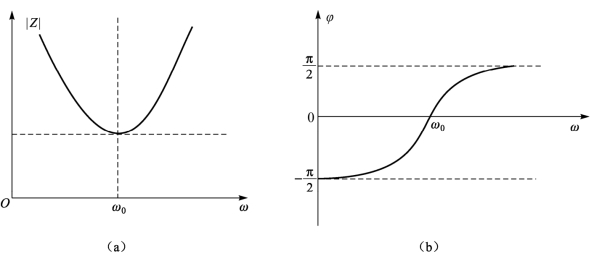
图6-4　串联谐振电路的频率特性曲线

2.电流谐振曲线

如图6-3所示串联谐振电路中，回路电流为

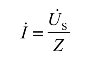(www.daowen.com)

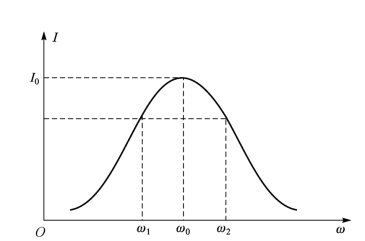
图6-5　电流谐振曲线

它的有效值为

由图6-4和式（6.14）可以看出，随ω变化，导致回路电流有效值的大小亦随ω 变化而变化。串联谐振回路中电流有效值大小随电源频率变化的曲线称为串联谐振回路的电流幅频曲线，又称电流谐振曲线（resonance curve）。如图6-5所示即为RLC串联谐振电路的电流谐振曲线。

从图6-5可以看出，当ω=ω0时，回路电流达到最大值，即当ω 偏离ω0时，电流下降。

3.通用电流谐振曲线

将式（6.12）代入式（6.14）可得

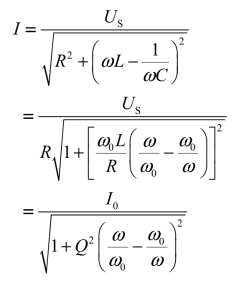
再整理得

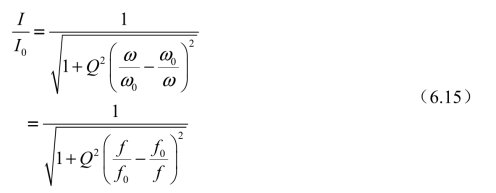
根据式（6.15），并以ω/ω0为自变量、以I/I0为因变量、以不同品质因数Q为参变量作出的谐振曲线称为通用电流谐振曲线，如图6-6所示。由图6-6可以看出，Q值高，曲线就尖锐；Q值低，曲线就平坦。即曲线的尖锐度与Q值成正比。

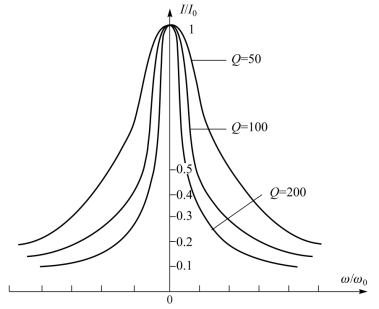
图6-6　通用电流谐振曲线