（1）随时间按正弦规律变化的交流电称为正弦交流电，又称为正弦量。

（2）正弦量的三要素。

最大值，如Um、Im，U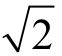m=U，Im=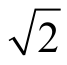I（即正弦量的最大值是有效值的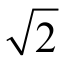倍）。

角频率ω，ω=2πf，ω=2π/T。

初相ψ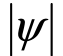，≤π。

（3）正弦量的表示法。

在确定的参考方向下，正弦量有四种表示方法，以正弦电流为例：

解析式，如i=Imsin （ω t+ψi）；

波形图；

相量表示法，如有效值相量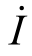=I∠ψi，振幅相量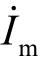=Im∠ψi；

相量图。

（4）两个同频率正弦量的相位关系。

两个同频率正弦量的相位差φ 等于两个正弦量的初相之差，即φ=ψ1-ψ2，且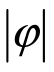≤π。根据相位差φ 的大小可以比较两个同频率正弦量的相位关系。(www.daowen.com)

0＜ψ1-ψ2＜π：第一个正弦量超前于第二个正弦量。

-π＜ψ1-ψ2＜0：第一个正弦量滞后于第二个正弦量。

ψ1-ψ2=0：这两个正弦量同相。

ψ1-ψ2=±π：这两个正弦量反相。

ψ1-ψ2=±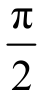：这两个正弦量正交。

（5）正弦量的相量图。

只有同频率的正弦量其相量才能画在同一复平面上，画在同一复平面上表示相量的图称为相量图。

（6）用相量法求同频率正弦量之和。

用相量表示正弦量进行交流电路运算的方法称为相量法。

（7）参考正弦量和参考相量。

为了简化正弦交流电路的分析计算，常假设某一正弦量的初相为零，该正弦量叫作参考正弦量，其相量形式称为参考相量。