RLC串联电路电压与电流的相量关系

如图4-35（a）所示为RLC串联电路，选定有关各量的参考方向并标于图4-35（a）上，RLC串联电路的相量模型如图4-35（b）所示。

由于是串联电路，电路中流过各元件的是同一个电流i，所以取i为参考正弦量，对应的相量为参考相量，即

电阻、电感、电容元件上的电压分别为

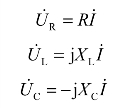
由KVL得

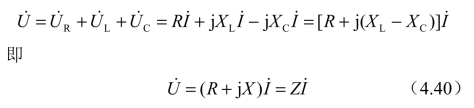
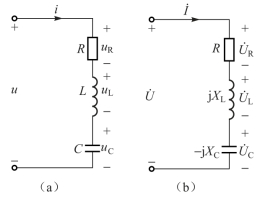
图4-35　RLC串联电路及相量模型

式（4.40）为RLC串联电路欧姆定律的相量形式，也就是伏安特性的相量形式，它既表示了电路中总电压和电流的有效值的关系，又表示了总电压和电流的相位关系。

式（4.40）中，X=XL-XC称为电路的电抗（reactance），其值可为正也可为负。而

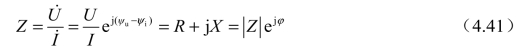
称为电路的复阻抗（complex impedance），表征电路中所有元件对电流的阻碍作用。Z是一个复数，实部是R，虚部是电抗X，单位为欧姆。但Z不是相量，因此只用大写字母Z表示而不加黑点。

从式（4.41）可以看出

其中，为复阻抗的模，称为电路的阻抗，它表示了电路中总电压和电流的有效值的关系；φ为复阻抗的辐角，称为阻抗角，它表示了总电压超前于电流的角度。

由于电抗X=XL-XC，故X值的正负体现了电路中电感与电容所起作的用角的度大。小，它决定阻抗角φ 的正负，关系到电路的性质。

RLC串联电路有以下三种不同的性质：

①当电路中电感的作用大于电容的作用，即时，XL＞XC，此时X ＞0，UL＞UC。阻抗角φ ＞0。以为参考相量，作出相量图如图4-36（a）所示（图中，为电抗电压相量，其大小为UX=UL-UC）。从相量图中可以看出，总电压超前于电流的角度为φ，电路呈感性。(www.daowen.com)

RLC串联电路电压与 电流的相量图

② 当电路中电容的作用大于电感的作用，即时，XL＜XC，此时X＜0，UL＜UC。阻抗角φ ＜0。以I˙为参考相量，作出相量图如图4-36（b）所示（图中电抗电压相量的大小为UX=UC-UL）。从相量图中可以看出，总电压滞后于电流的角度为，电路呈容性。

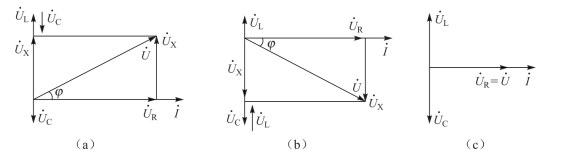
图4-36　RLC串联电路的相量图

③当ωL=时，XL=XC，此时X=0，UL=UC，阻抗角φ=0。其相量图如图4-36（c）所示，此时电路中电容的作用和电感的作用相互抵消，电流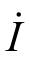和电压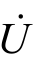同相，电路呈阻性。这是串联电路的一种特殊状态，称作“串联谐振”，将在第6章中进一步讨论。

显然，在图4-36（a）、（b）中，组成一个直角三角形，称为电压三角形，如图4-37所示，其中图（a）为感性电路的电压三角形，图（b）为容性电路的电压三角形。电压三角形反映了各个正弦电压有效值和相位之间的关系。由两个电压三角形可知，U≠UR+UL+UC，阻抗角φ 反映了在关联参考方向下总电压超前电流的角度。

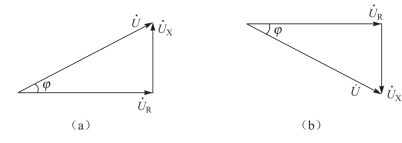
图4-37　RLC串联电路的电压三角形

以图4-37（a）为例，根据勾股定理，总电压和各个分电压之间的关系为

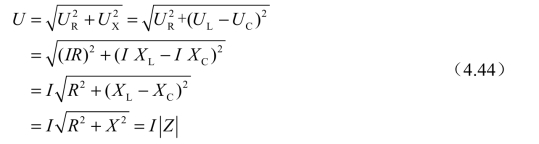
由式（4.44）可知，即阻抗反映了电路总电压和电流有效值之间的关系。

若将电压三角形的三条边同除以电流I，就得到一个新的三角形，它与电压三角形相似，反映了电阻R、电路的电抗X和阻抗之间的数值关系，因此称为阻抗三角形（见图4-38）。应注意的是，阻抗三角形不是相量三角形。从阻抗三角形可以看出阻抗角φ 是阻抗和电阻R之间的夹角。阻抗和阻抗角φ与电路的R、L、C参数及频率有关，而与电压、电流无关。

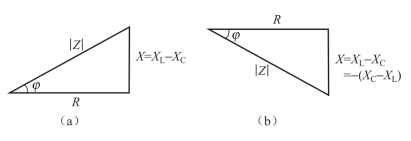
图4-38　RLC串联电路的阻抗三角形

任何无源二端网络和无源二端元件都可以引入它的复阻抗，端口伏安特性的相量形式都可以用式（4.40），即表示。RL串联电路、RC串联电路、电阻元件、电感元件、电容元件都可以看成RLC串联电路的特例。

R、L、C的复阻抗Z分别为R、jXL、-jXC，阻抗角φ 分别为0、90°、-90°。

RL串联电路复阻抗Z为R+jXL、阻抗角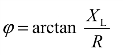

RC串联电路复阻抗Z为R-jXC、阻抗角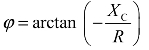

由RLC串联各阻抗的关系，可以推广到阻抗串联的一般情况，其等效阻抗等于各串联阻抗之和。